11.10: Collision Theory
- Page ID
- 84593
Collision Theory was first introduced in the 1910s by Max Trautz (Trautz, 1916) and William Lewis (Lewis, 1918) to try to account for the magnitudes of rate constants in terms of the frequency of molecular collisions, the collisional energy, and the relative orientations of the molecules involved in the collision.
The rate of a reaction, according to collision theory, can be expressed as
\[ \text{rate} = Z_{ab} F \label{majorrate} \]
where \(Z_{AB}\) is the frequency of collisions between the molecules \(A\) and \(B\) involved in the reaction, and \(F\) is the fraction of those collisions that will lead to a reaction. The factor \(F\) has two important contributors, the energy of the collision and the orientation of the molecules when they collide. The first term, \(Z_{AB}\), can be taken from the kinetic molecular theory discussed in Chapter 2.
\[ Z_{AB} = \left( \dfrac{8k_BT}{\pi \mu} \right)^{1/2} \sigma_{AB} [A][B] \label{collision} \]
Where the first term is the average relative velocity in which \(\mu\) is the reduced mass of the A-B collisional system, \(\sigma_{AB}\) is the collisional cross section, and \([A]\) and \([B]\) are the concentrations of \(A\) and \(B\).
The factor \(F\) depends on the activation energy. Assuming a Boltzmann (or Boltzmann-like) distribution of energies, the fraction of molecular collisions that will have enough energy to overcome the activation barrier is given by
\[ F= e^{-E_a/RT} \label{arr} \]
Combining Equations \ref{collision} and \ref{arr}, the rate of the reaction (Equation \ref{majorrate}) is predicted by
\[ \text{rate} = \left( \dfrac{8k_BT}{\pi \mu} \right) ^{1/2} \sigma_{AB} e^{-E_a/RT} [A][B] \nonumber \]
So if the rate law can be expressed as a second order rate law
\[\text{rate} = k [A][B] \nonumber \]
it is clear that the rate constant \(k\) is given by
\[k=\left( \dfrac{8k_BT}{\pi \mu} \right)^{1/2} \sigma_{AB} e^{-E_a/RT} \nonumber \]
By comparison, the theory predicts the form of the Arrhenius prefactor to be
\[A= \left( \dfrac{8k_BT}{\pi \mu} \right)^{1/2} \sigma_{AB} \nonumber \]
It should be noted that collision theory appears to apply only to bimolecular reactions, since it takes two molecules to collide. But there are many reactions that have first order rate laws, but are initiated by bimolecular steps in the mechanisms. (Reaction mechanisms will form a large part of the discussion in Chapter 12.) Consider as an example, the decomposition of \(N_2O_5\), which follows the reaction
\[2 N_2O_5 \rightarrow 4 NO_2 + O_2 \nonumber \]
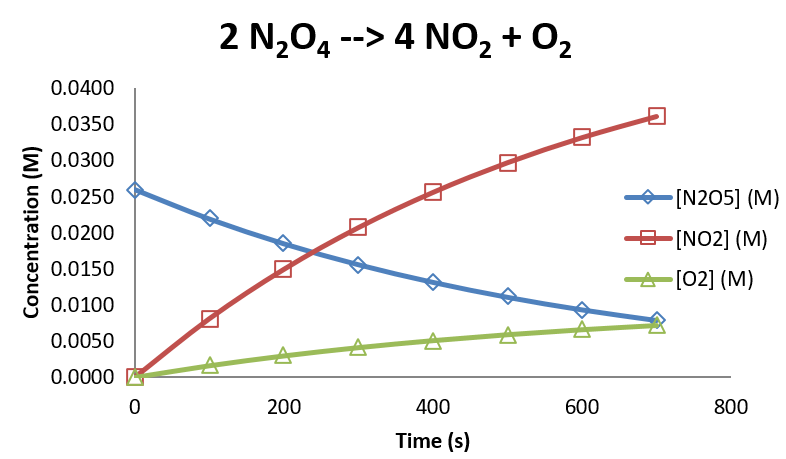
Under a certain set of conditions, the following concentrations are observed as a function of time.
| time (s) | \([N_2O_5]\) (M) | \([NO_2]\) (M) | \([O_2]\) (M) |
|---|---|---|---|
| 0 | 0.0260 | 0.0000 | 0.0000 |
| 100 | 0.0219 | 0.0081 | 0.0016 |
| 200 | 0.0185 | 0.0150 | 0.0030 |
| 300 | 0.0156 | 0.0207 | 0.0041 |
| 400 | 0.0132 | 0.0256 | 0.0051 |
| 500 | 0.0111 | 0.0297 | 0.0059 |
| 600 | 0.0094 | 0.0332 | 0.0066 |
| 700 | 0.0079 | 0.0361 | 0.0072 |
Graphically, these data look as follows:
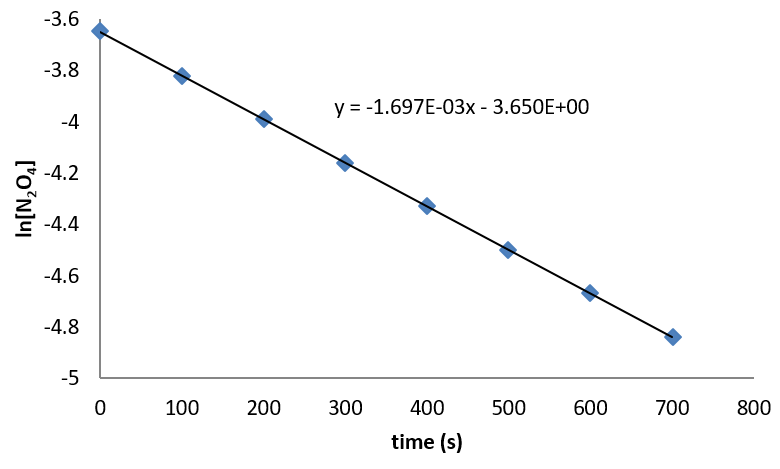
The data for N2O5 can be analyzed empirically to show that the reaction is first order in N2O5, with a rate constant of 1.697 x 10-3 s-1. (The graph is shown below.) So the rate law for the reaction is
\[\text{rate} = 1.697 \times 10^{-3}s^{-1} [N_2O_5] \nonumber \]
So how can collision theory be used to understand the rate constant? As it turns out, the mechanism for the reaction involves a bimolecular initiation step.
The mechanism for the reaction has a bimolecular initiation step
\[ N_2O_5 + M \rightleftharpoons N_2O_5^* + M \nonumber \]
where \(N_2O_5^*\) is an energetically activated form of \(N_2O_5\) which can either relax to reform \(N_2O_5\) or decompose to form the products of the reaction. Because the initiation step is bimolecular, collision theory can be used to understand the rate law, but because the product of the unimolecular step undergoes slow conversion to products unimolecularly, the overall rate is observed to be first order in \(N_2O_5\). The analysis of reaction mechanisms, and reconciliation with observed rate laws, form the subjects of Chapter 12.


