2.7: Appendix- Third-order diagrams for a four-level system
- Page ID
- 304367
The third order response function can describe interaction with up to four eigenstates of the system Hamiltonian. These are examples of correlation functions within \(R^{(3)}\) for a four-level system representative of vibronic transitions accompanying an electronic excitation, as relevant to resonance Raman spectroscopy. Note that these diagrams present only one example of multiple permutations that must be considered given a particular time-sequence of incident fields that may have variable frequency.
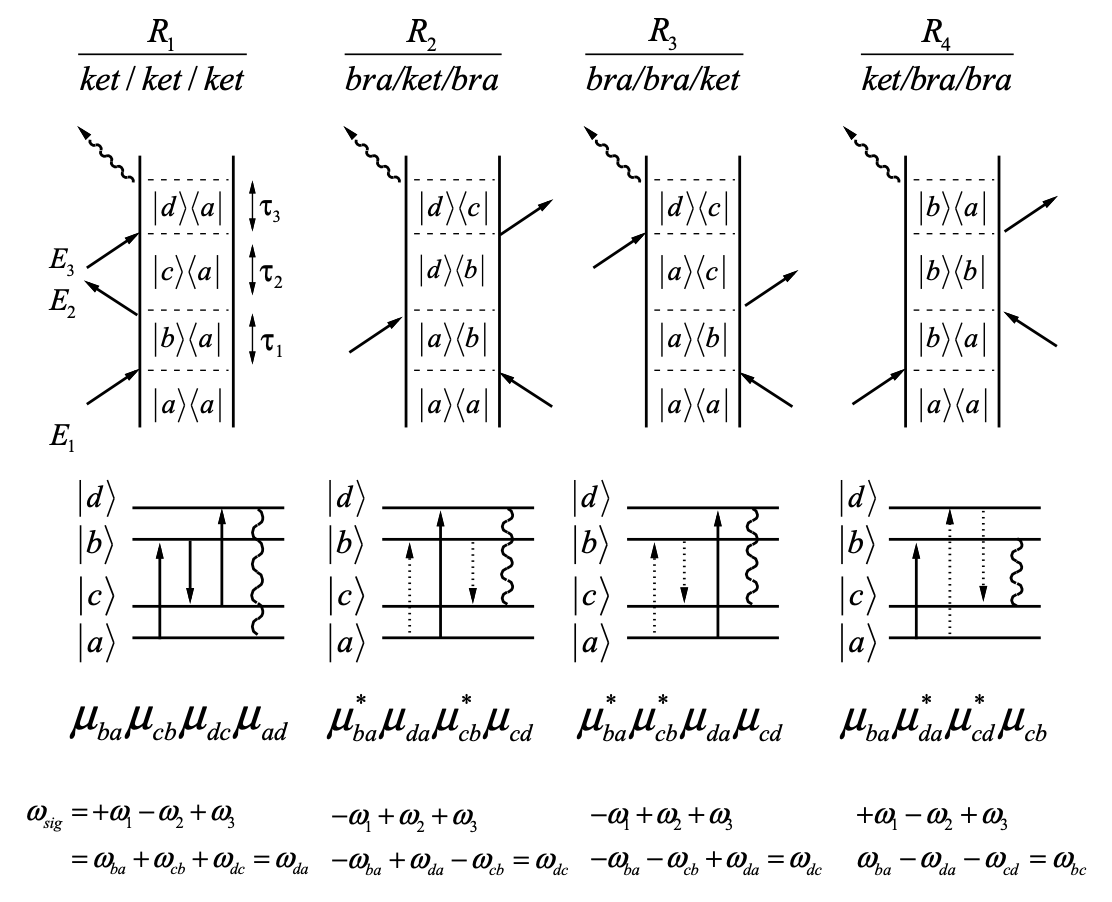
The signal frequency comes from summing all incident resonance frequencies accounting for the sign of the excitation. The products of transition matrix elements are written in a time-ordered fashion without the projection onto the incident field polarization needed to properly account for orientational effects. The \(R_1\) term is more properly written \(\langle\left(\bar\mu_{ba}\cdot\hat\epsilon_1\right)\left(\bar\mu_{cb}\cdot\hat\epsilon_2\right)\left(\bar\mu_{dc}\cdot\hat\epsilon_3\right)\left(\bar\mu_{ad}\cdot\hat\epsilon_{an}\right)\rangle\). Note that the product of transition dipole matrix elements obtained from the sequence of interactions can always be re-written in the cyclically invariant form \(\mu_{ab}\mu_{bc}\mu_{cd}\mu_{da}s\). This is one further manifestation of closed loops formed by the sequence of interactions.

