15.1: Definitions

Last updated
Save as PDF

Page ID: 106896

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

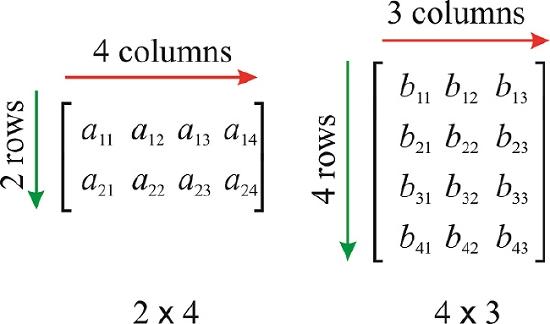
An \(m\times n\) matrix \(\mathbf{A}\) is a rectangular array of numbers with \(m\) rows and \(n\) columns. The numbers \(m\) and \(n\) are the dimensions of \(\mathbf{A}\). The numbers in the matrix are called its entries. The entry in row \(i\) and column \(j\) is called \(a_{ij}\).

Figure \(\PageIndex{1}\): Matrices of different dimensions (CC BY-NC-SA; Marcia Levitus)

Some types of matrices have special names:

A square matrix:\[\begin{pmatrix} 3 &-2 &4 \\ 5 &3i &3 \\ -i & 1/2 &9 \end{pmatrix} \nonumber\] with \(m=n\)
A rectangular matrix:\[\begin{pmatrix} 3 &-2 &4 \\ 5 &3i &3 \end{pmatrix}\nonumber\] with \(m\neq n\)
A column vector:\[\begin{pmatrix} 3 \\ 5\\ -i \end{pmatrix}\nonumber\] with \(n=1\)
A row vector:\[\begin{pmatrix} 3 &-2 &4 \\ \end{pmatrix}\nonumber\] with \(m=1\)
The identity matrix:\[\begin{pmatrix} 1 &0 &0 \\ 0 &1 &0 \\ 0&0 &1 \end{pmatrix}\nonumber\] with \(a_{ij}=\delta_{i,j}\), where \(\delta_{i,j}\) is a function defined as \(\delta_{i,j}=1\) if \(i=j\) and \(\delta_{i,j}=0\) if \(i\neq j\).
A diagonal matrix:\[\begin{pmatrix} a &0 &0 \\ 0 &b &0 \\ 0&0 &c \end{pmatrix}\nonumber\] with \(a_{ij}=c_i \delta_{i,j}\).
An upper triangular matrix:\[\begin{pmatrix} a &b &c \\ 0 &d &e \\ 0&0 &f \end{pmatrix}\nonumber\] All the entries below the main diagonal are zero.
A lower triangular matrix:\[\begin{pmatrix} a &0 &0 \\ b &c &0 \\ d&e &f \end{pmatrix}\nonumber\] All the entries above the main diagonal are zero.
A triangular matrix is one that is either lower triangular or upper triangular.

The Trace of a Matrix

The trace of an \(n\times n\) square matrix \(\mathbf{A}\) is the sum of the diagonal elements, and formally defined as \(Tr( \mathbf{A})=\sum_{i=1}^{n}a_{ii}\).

For example,

\[\mathbf{A}=\begin{pmatrix} 3 &-2 &4 \\ 5 &3i &3 \\ -i & 1/2 &9 \end{pmatrix}\; ; Tr(\mathbf{A})=12+3i \nonumber\]

Singular and Nonsingular Matrices

A square matrix with nonzero determinant is called nonsingular. A matrix whose determinant is zero is called singular. (Note that you cannot calculate the determinant of a non-square matrix).

The Matrix Transpose

The matrix transpose, most commonly written \(\mathbf{A}^T\), is the matrix obtained by exchanging \(\mathbf{A}\)’s rows and columns. It is obtained by replacing all elements \(a_{ij}\) with \(a_{ji}\). For example:

\[\mathbf{A}=\begin{pmatrix} 3 &-2 &4 \\ 5 &3i &3 \end{pmatrix}\rightarrow \mathbf{A}^T=\begin{pmatrix} 3 &5\\ -2 &3i\\ 4&3 \end{pmatrix} \nonumber\]