14.3: The Vector Product
- Page ID
- 106892
The vector product of two vectors is a vector defined as
\[\mathbf{u}\times \mathbf{v}=|\mathbf{u}| |\mathbf{v}| \mathbf{n} \sin\theta \nonumber\]
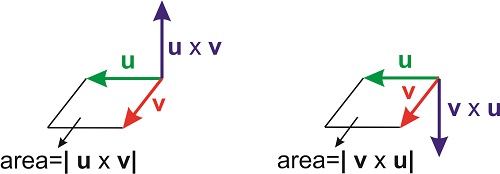
where \(\theta\) is again the angle between the two vectors, and \(\mathbf{n}\) is the unit vector perpendicular to the plane formed by \(\mathbf{u}\) and \(\mathbf{v}\). The direction of the vector \(\mathbf{n}\) is given by the right-hand rule. Extend your right hand and point your index finger in the direction of \(\mathbf{u}\) (the vector on the left side of the \(\times\) symbol) and your forefinger in the direction of \(\mathbf{v}\). The direction of \(\mathbf{n}\), which determines the direction of \(\mathbf{u}\times \mathbf{v}\), is the direction of your thumb. If you want to revert the multiplication, and perform \(\mathbf{v}\times \mathbf{u}\), you need to point your index finger in the direction of \(\mathbf{v}\) and your forefinger in the direction of \(\mathbf{u}\) (still using the right hand!). The resulting vector will point in the opposite direction (Figure \(\PageIndex{1}\)).
The magnitude of \(\mathbf{u}\times \mathbf{v}\) is the product of the magnitudes of the individual vectors times \(\sin \theta\). This magnitude has an interesting geometrical interpretation: it is the area of the parallelogram formed by the two vectors (Figure \(\PageIndex{1}\)).
The cross product can also be expressed as a determinant:
\[\mathbf{u}\times \mathbf{v}= \begin{vmatrix} \hat{\mathbf{i}}&\hat{\mathbf{j}}&\hat{\mathbf{k}}\\ u_x&u_y&u_z\\ v_x&v_y&v_z\\ \end{vmatrix} \nonumber\]
Given \(\mathbf{u}=-2 \hat{\mathbf{i}}+\hat{\mathbf{j}}+\hat{\mathbf{k}}\) and \(\mathbf{v}=3 \hat{\mathbf{i}}-\hat{\mathbf{j}}+\hat{\mathbf{k}}\), calculate \(\mathbf{w}=\mathbf{u}\times \mathbf{v}\) and verify that the result is perpendicular to both \(\mathbf{u}\) and \(\mathbf{v}\).
Solution
\[ \begin{align*} \mathbf{u}\times \mathbf{v} &= \begin{vmatrix} \hat{\mathbf{i}}&\hat{\mathbf{j}}&\hat{\mathbf{k}}\\ u_x&u_y&u_z\\ v_x&v_y&v_z\\ \end{vmatrix}=\begin{vmatrix} \hat{\mathbf{i}}&\hat{\mathbf{j}}&\hat{\mathbf{k}}\\ -2&1&1\\ 3&-1&1\\ \end{vmatrix} \\[4pt] &=\hat{\mathbf{i}}(1+1)-\hat{\mathbf{j}}(-2-3)+\hat{\mathbf{k}}(2-3) \\[4pt] &=\displaystyle{\color{Maroon}2 \hat{\mathbf{i}}+5 \hat{\mathbf{j}}-\hat{\mathbf{k}}} \end{align*} \nonumber\]
To verify that two vectors are perpendicular we perform the dot product:
\[\mathbf{u} \cdot \mathbf{w}=(-2)(2)+(1)(5)+(1)(-1)=0 \nonumber\]
\[\mathbf{v} \cdot \mathbf{w}=(3)(2)+(-1)(5)+(1)(-1)=0 \nonumber\]
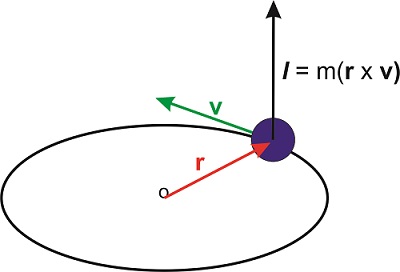
An important application of the cross product involves the definition of the angular momentum. If a particle with mass \(m\) moves a velocity \(\mathbf{v}\) (a vector), its (linear) momentum is \(\mathbf{p}=m\mathbf{v}\). Let \(\mathbf{r}\) be the position of the particle (another vector), then the angular momentum of the particle is defined as
\[\mathbf{l}=\mathbf{r}\times\mathbf{p} \nonumber\]
The angular momentum is therefore a vector perpendicular to both \(\mathbf{r}\) and \(\mathbf{p}\). Because the position of the particle needs to be defined with respect to a particular origin, this origin needs to be specified when defining the angular momentum.