14.1: Introduction to Vectors
- Page ID
- 106890
In this chapter we will review a few concepts you probably know from your physics courses. This chapter does not intend to cover the topic in a comprehensive manner, but instead touch on a few concepts that you will use in your physical chemistry classes.
A vector is a quantity that has both a magnitude and a direction, and as such they are used to specify the position, velocity and momentum of a particle, or to specify a force. Vectors are usually denoted by boldface symbols (e.g. \(\mathbf{u}\)) or with an arrow above the symbol (e.g. \(\vec{u}\)). A tilde placed above or below the name of the vector is also commonly used in shorthand (\(\widetilde{u}\),\(\underset{\sim}{u}\)).
If we multiply a number \(a\) by a vector \(\mathbf{v}\), we obtain a new vector that is parallel to the original but with a length that is \(a\) times the length of \(\mathbf{v}\). If \(a\) is negative \(a\mathbf{v}\) points in the opposite direction than \(\mathbf{v}\). We can express any vector in terms of the so-called unit vectors. These vectors, which are designated \(\hat{\mathbf{i}}\), \(\hat{\mathbf{j}}\) and \(\hat{\mathbf{k}}\), have unit length and point along the positive \(x, y\) and \(z\) axis of the cartesian coordinate system (Figure \(\PageIndex{1}\)). The symbol \(\hat{\mathbf{i}}\) is read "i-hat". Hats are used to denote that a vector has unit length.
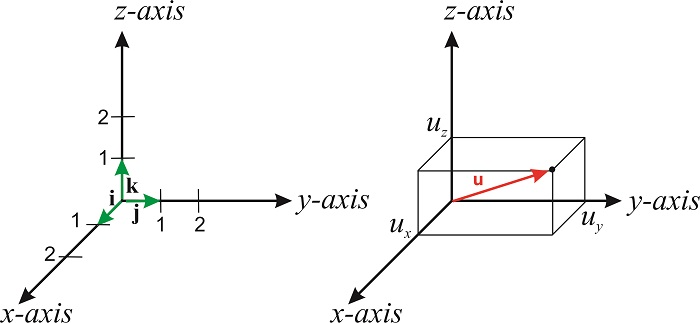
The length of \(\mathbf{u}\) is its magnitude (or modulus), and is usually denoted by \(u\):
\[\label{eq:vectors1} u=|u|=(u_x^2+u_y^2+u_z^2)^{1/2}\]
If we have two vectors \(\mathbf{u}=u_x\hat{\mathbf{i}}+u_y \hat{\mathbf{j}}+u_z \hat{\mathbf{k}}\) and \(\mathbf{v}=v_x \hat{\mathbf{i}}+v_y \hat{\mathbf{j}}+v_z \hat{\mathbf{k}}\), we can add them to obtain
\[\mathbf{u}+\mathbf{v}=(u_x+v_x)\hat{\mathbf{i}}+(u_y+v_y)\hat{\mathbf{j}}+(u_z+v_z)\hat{\mathbf{k}} \nonumber\]
or subtract them to obtain:
\[\mathbf{u}-\mathbf{v}=(u_x-v_x)\hat{\mathbf{i}}+(u_y-v_y)\hat{\mathbf{j}}+(u_z-v_z)\hat{\mathbf{k}} \nonumber\]
When it comes to multiplication, we can perform the product of two vectors in two different ways. The first, which gives a scalar (a number) as the result, is called scalar product or dot product. The second, which gives a vector as a result, is called the vector (or cross) product. Both are important operations in physical chemistry.


