12.5: Problems
- Page ID
- 106880
Find \(f(x, y)\). Note: In order to obtain all possible solutions in each case you will have to consider that the separation constant can be positive, negative, or zero.
- \(2 \frac{ \partial f}{ \partial x} + \frac{ \partial f}{ \partial y} = 0\)
- \(y \frac{ \partial f}{ \partial x} − x \frac{ \partial f}{ \partial y} = 0\)
- \( \frac{\partial^2 f}{ \partial x^2} + \frac{\partial^2 f}{\partial y^2} = 0\)
Consider a uniform string under tension and of length \(L\). At time \(t = 0\) the string is displaced as shown in the figure and released. The displacement of the string from its horizontal position \((u(x, t))\) depends on both \(x\) and \(t\) and satisfies the following PDE:
\[ \frac{ \partial^2 u(x, t)}{\partial x^2} = \frac{1}{v^2} \frac{\partial^2 u(x, t)}{\partial t^2}\]
where \(v\) is a constant that depends on the characteristics of the string.
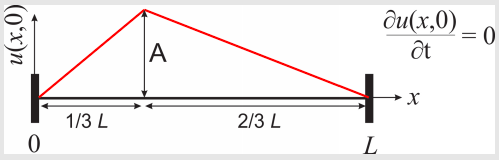
- Obtain an expression for \(u(x, t)\). Note that most of the problem is solved in the book, but you still need to show ALL steps.
- In the lab: Assume \(v = 440 \text{m/s}, ~ A = 5 \text{cm}\) and \(L = 12 \text{cm}\). Create a function \(u(x, t)\) with the result of 1). Remember that you can’t plot an infinite sum, so you will have to truncate it when plotting in Mathematica. Use the function "Manipulate" to generate an animation of the vibrating string. Be sure you run it slowly so you can see the motion).
Use the separation of variables method to obtain an expression for \(C(x, t)\) for the system described in Section 12.4:
\[ \frac{\partial^2 C(x,t)}{\partial x^2} = \frac{1}{D} \frac{\partial C(x,t)}{\partial t} \nonumber\]
\[\frac{\partial C(0,t)}{\partial x} = \frac{\partial C(L,t)}{\partial x} = 0 \nonumber\]
The solution is:
\[ C(x, t) = \sum_{n=0}^{\infty} a_n \cos \left( \frac{n \pi}{L} x \right)e^{− \left( \frac{n \pi}{L} \right)^2 Dt} \nonumber\]
where the coefficients \(a_n\) depend on the initial concentration profile (initial conditions).
Continue the previous problem and obtain the full expression of \(C(x, t)\) using the initial condition shown in Figure \(\PageIndex{1}\):
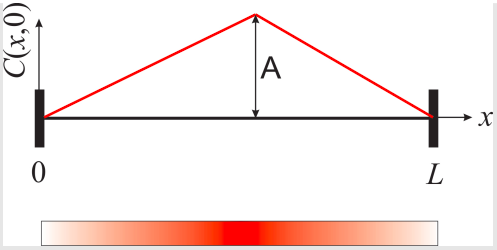
Figure \(\PageIndex{1}\): The initial concentration profile, \(C(x, 0)\). The diagram at the bottom represents a cartoon of what the tube would look like at time zero, with higher concentration of red dye at the center and zero concentration at both ends.
The even extension of this function is (compare with Figure \(12.3.6\))
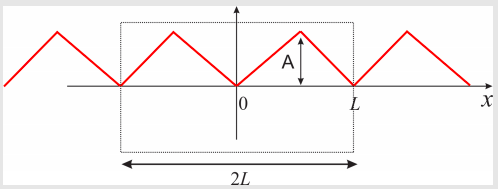
Figure \(\PageIndex{2}\): The even extension of y(x) (Figure \(\PageIndex{1}\)).
In the lab:
- Assume \(L = 1 \text{cm}, ~ A = 1 \text{M}\), and \(D = 6.510−10\text{m}^2/\text{s}\) (the diffusion coefficient of glucose in water) Use Manipulate to create a movie that shows how \(C(x)\) changes with time.
- Plot \(C(0, t)\) (that is, the concentration at the end of the tube as a function of time). How long does it take until the concentration reaches 0.1M? (give an approximate value). This should demonstrate the need of stirring your coffee after adding sugar (i.e. waiting until sugar diffuses on its own would take too long for you to enjoy a hot cup of coffee).
- Repeat the previous question assuming \(L = 1 \mu \text{m}\) (the order of magnitude of the diameter of the nucleus of a cell). This should demonstrate that diffusion is an efficient mechanism for molecular transport inside small cells like bacteria, or inside the nucleus of larger cells.


