9.7: Problems
- Page ID
- 107021
Determine whether the following differentials are exact or inexact. If they are exact, determine \(u=u(x,y)\).
- \(du=(2ax+by)dx+(bx+2cy)dy\)
- \(du=(x^2-y^2)dx+(2xy)dy\)
Determine whether dz is exact or inexact. If it is exact, determine \(z=z(P,T)\).
\[dz=-\frac{RT}{P^2}dP+\frac{R}{P}dT \nonumber \]
From Equation \ref{eq:dG}, and using the fact that \(G\) is a state function, prove that the change in entropy (\(\Delta S\)) of one mole of an ideal gas whose pressure changes from an initial value \(P_1\) to a final value \(P_2\) at constant temperature is:
\[\Delta S =-R \ln{\frac{P_2}{P_1}}\nonumber \]
From Equations \ref{eq:dU}-\ref{eq:dA}, and using the fact that \(U,H\) and \(A\) are state functions, derive the three corresponding Maxwell relations.
- Answer
-
Add texts here. Do not delete this text first.
Given the following differential:
\[dz=xy dx + 2y dy\nonumber \]
- Determine if it is exact or inexact. If it is, obtain \(z(x,y)\)
- Calculate the line integrals \(\int_c{dz}\) for the paths enumerated below:
- the line \(y=2x\) from \(x=0\) to \(x=2\)
- the curve \(y = x^2\) from \(x = 0\) to \(x = 2\)
- any other path of your choice that joins the same initial and final points.
For a mole of a perfect monoatomic gas, the internal energy can be expressed as a function of the pressure and volume as
\[U = \frac{3}{2}PV\nonumber\]
- Write the total differential of \(U\), \(dU\).
- Calculate the line integrals \(\int_c{dU}\) for the paths shown below (\(c_1, c_2, c_3\)):
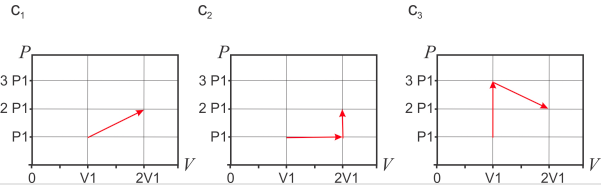
- Calculate \(U(V_f,P_f)-U(V_i,P_i)\) and compare with the results of b) (Note: \(f\) refers to the final state and \(i\) to the initial state).
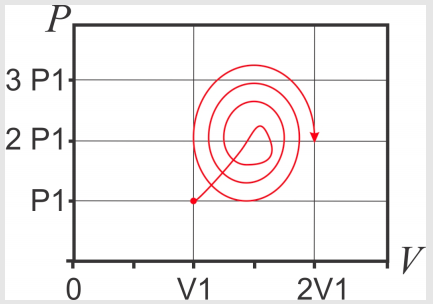
- Considering your previous results, calculate \(\int_c{dU}\) for the path below:
As defined in Section 9.3,
\[\label{eq:dU} dU=T(S,V)dS-P(S,V)dV\]
\[\label{eq:dP} dH=T(S,P)dS+V(S,P)dP\]
\[\label{eq:dA} dA=-S(T,V)dT-P(T,V)dV\]
\[\label{eq:dG} dG=-S(T,P)dT+V(T,P)dP\]


