9.5: Line Integrals
- Page ID
- 106859
In Section 9.1, we discussed that in order to properly calculate the change in pressure we would need to integrate the differential defined in Equation \ref{eq:differentials1}:
\[dP=\left (\dfrac{\partial P}{\partial V} \right )_{T,n} dV+\left (\dfrac{\partial P}{\partial T} \right )_{V,n} dT \label{eq:differentials1}\]
This raises the question of how to integrate differentials such as this one. Before we focus on this question, let’s discuss what we expect for an exact differential. Let’s say that we know how to perform these integrals, and we integrate \(dP\) from initial pressure (\(P_i\)) to final pressure (\(P_f\)) to calculate \(\Delta P\) for a change that is not infinitesimal:
\[ \Delta P = \int_{P_i}^{P_f} dP \nonumber\]
Would it surprise you that the result equals the final pressure minus the initial pressure?
\[ \Delta P = P_f - P_i \nonumber\]
Hopefully not; the change in pressure will obviously be the final pressure minus the initial pressure, regardless of whether we did this slowly, fast, at constant volume, constant temperature, etc. In other words, you just need the information of the state of the system at the beginning and the end of the process, but you do not need to know anything about what happened in between. All this makes sense because \(P\) is a state function, and the same argument applies to other state functions, such as entropy, internal energy, free energy, etc. We just reached an important conclusion: if we integrate an exact differential, the result will be independent of the path, and it will equal the function at the end point minus the function at the initial point. If we integrate an inexact differential this is not true, because we will be integrating the differential of a function that is not a state function. We’ll come back to this many times, but it is important that before getting lost in the math we keep in mind what to expect.
We already mentioned the word “path”, but what do we mean by that? In the example of the gas, the path would be described by the values of the temperature and volume at all times. For example, Figure \(\PageIndex{1}\) shows two possible paths that result in the same change in pressure. We could imagine an infinite number of other options, and of course we are not restricted to keeping one variable constant while changing the other.
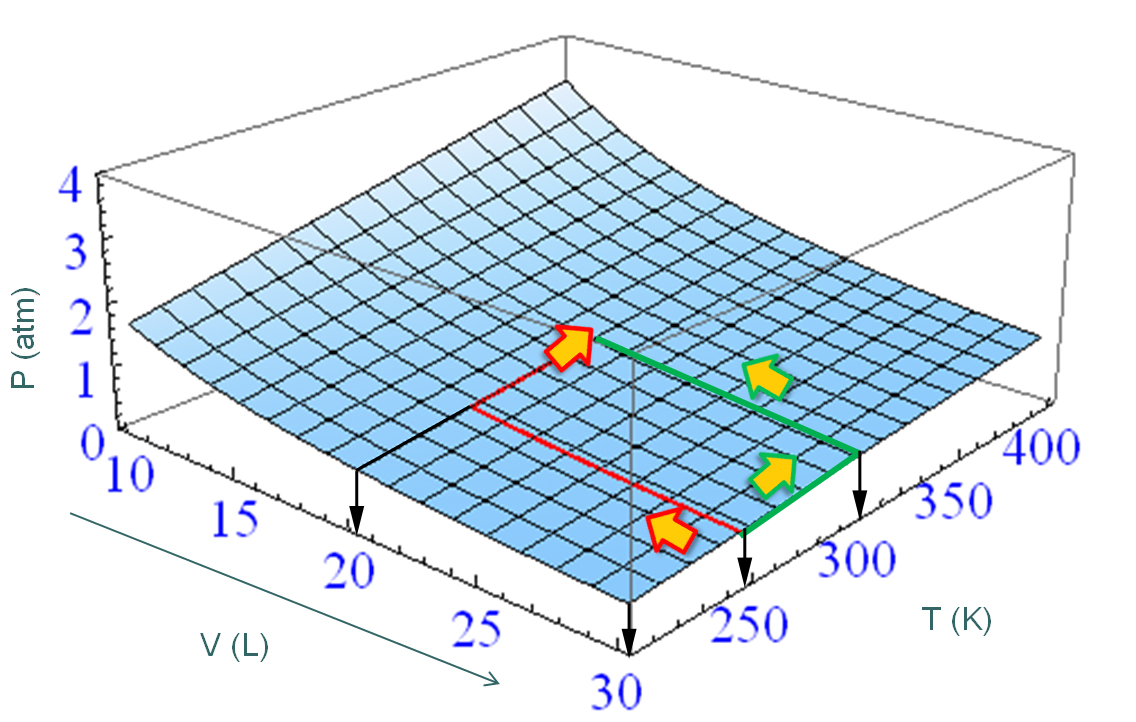
We can integrate \(dP\) along one path or the other, but we already know what we will get: \(\int dP = P_2-P_1\) regardless of the path. Work and heat, on the other hand, are not state functions. There is no such a thing as an amount of work or heat in a system. The amounts of heat and work that “flow” during a process connecting specified initial and final states depend on how the process is carried out. This means that if we want to calculate the work or the heat involved in the process, we would need to integrate the inexact differentials \(dw\) and \(dq\) indicating the particular path used to take the system from the initial to the final states:
\[q=\int\limits_{path} dq \nonumber\]
\[w=\int\limits_{path} dw \nonumber\]
For one mole of an ideal gas (\(P = RT/V\)),
\[dP=\left (\dfrac{\partial P}{\partial V} \right )_{T,n} dV+\left (\dfrac{\partial P}{\partial T} \right )_{V,n} dT=-\dfrac{RT}{V^2}dV+\dfrac{R}{V} dT \nonumber\]
From our previous discussion, we know the result of integrating the differential
\[dP=-\dfrac{RT}{V^2}dV+\dfrac{R}{V} dT \nonumber\]
along any path. The result should be the final pressure minus the initial pressure:
\[\label{eq:diff17} \Delta P=R(T_f/V_f-T_i/V_i)\]
where the subscripts \(f\) and \(i\) refer to the final and initial states.
Even is we know the answer, let’s do it anyway so we learn how to integrate differentials. We will consider the two paths depicted in Figure \(\PageIndex{1}\). In both cases the initial temperature is 250 K, the initial volume is 30 L, the final temperature is 300 K, and the final volume is 20 L.
Let’s start with the ‘red’ path. This path is the sum of two components, one where we change the volume at constant temperature, and another one where we change the temperature at constant volume. Let’s call these individual steps path 1 and path 2, so the total path is path1 + path 2:
\[\int\limits_{path}dP=\int\limits_{path 1}dP+\int\limits_{path 2}dP \nonumber\]
\[\int\limits_{path}{\left(-\dfrac{RT}{V^2}dV+\dfrac{R}{V} dT\right)}=\int\limits_{path 1}\left(-\dfrac{RT}{V^2}dV+\dfrac{R}{V} dT\right)+\int\limits_{path 2}\left(-\dfrac{RT}{V^2}dV+\dfrac{R}{V} dT\right) \nonumber\]
In path 1, we keep the temperature constant, so \(dT=0\). Furthermore, the temperature equals \(T_i\) during the whole process:
\[\int\limits_{path 1}\left(-\dfrac{RT}{V^2}dV+\dfrac{R}{V} dT\right)=\int\limits_{path 1}\left(-\dfrac{RT_i}{V^2}dV\right)=\int_{V_i}^{V_f}-\dfrac{RT_i}{V^2}dV \nonumber\]
in path 2 we keep the volume constant, so \(dV=0\). Furthermore, the volume equals \(V_f\) during the whole process:
\[\int\limits_{path 2}\left(-\dfrac{RT}{V^2}dV+\dfrac{R}{V} dT\right)=\int\limits_{path 2}\dfrac{R}{V_f} dT=\int_{T_i}^{T_f}\dfrac{R}{V_f} dT \nonumber\]
Putting the two results together:
\[\int\limits_{path}\left(-\dfrac{RT}{V^2}dV+\dfrac{R}{V} dT\right)=\int_{V_i}^{V_f}-\dfrac{RT_i}{V^2}dV+\int_{T_i}^{T_f}\dfrac{R}{V_f} dT \nonumber\]
\[\int\limits_{path}\left(-\dfrac{RT}{V^2}dV+\dfrac{R}{V} dT\right)=\left. \dfrac{RT_i}{V}\right|_{V_i}^{V_f}+\left. \dfrac{RT}{V_f}\right|_{T_i}^{T_f}=RT_i\left(\dfrac{1}{V_f}-\dfrac{1}{V_i}\right)+\dfrac{R}{V_f}(T_f-T_i) \nonumber\]
\[RT_i\left(\dfrac{1}{V_f}-\dfrac{1}{V_i}\right)+\dfrac{R}{V_f}(T_f-T_i)=R\left(\dfrac{T_i}{V_f}-\dfrac{T_i}{V_i}+\dfrac{T_f}{V_f}-\dfrac{T_i}{V_f} \right)=R\left(\dfrac{T_f}{V_f}-\dfrac{T_i}{V_i}\right) \nonumber\]
The result is, as expected, identical to Equation \ref{eq:diff17}.
Let’s now consider the two-step path depicted in green in Figure \(\PageIndex{1}\). We’ll follow the same ideas we used for the path shown in red. In the first part of the path we change the temperature from \(T_i\) to \(T_f\) at constant volume, \(V=V_i\). In the second part of the path we change the volume from \(V_i\) to \(V_f\) at constant temperature, \(T=T_f\). In the first part, \(dV=0\) and \(V=V_i\) at all times. In the second part, \(dT=0\), and \(T=T_f\) at all times:
\[\int\limits_{path}\left(-\dfrac{RT}{V^2}dV+\dfrac{R}{V} dT\right)=\int_{T_i}^{T_f}\left(\dfrac{R}{V_i} dT\right)+\int_{V_i}^{V_f}\left(-\dfrac{RT_f}{V^2}dV\right) \nonumber\]
\[\int\limits_{path}\left(-\dfrac{RT}{V^2}dV+\dfrac{R}{V} dT\right)=\left. \dfrac{RT}{V_i}\right|_{T_i}^{T_f}+\left. \dfrac{RT_f}{V}\right|_{V_i}^{V_f} \nonumber\]
\[\int\limits_{path}\left(-\dfrac{RT}{V^2}dV+\dfrac{R}{V} dT\right)=\dfrac{R}{V_i}(T_f-T_i)+RT_f\left(\dfrac{1}{V_f}-\dfrac{1}{V_i}\right)=R\left(\dfrac{T_f}{V_f}-\dfrac{T_i}{V_i}\right) \nonumber\]
The result is, as expected, \(P_f-P_i\) (Equation \ref{eq:diff17}).
Because \(dP\) is exact, it does not matter which path we choose to go from \((V_i,P_i)\) to \((V_f,P_f)\), the result of the integral of \(dP\) will always the same \(R\left(\dfrac{T_f}{V_f}-\dfrac{T_i}{V_i}\right)\). Let’s try another path; this time one that does not keep any of the variables constant at any time. Consider the path that is the straight line that joins the points \((V_i,P_i)\) to \((V_f,P_f)\). In order to integrate \(dP\) along a particular path, we need the equation of the path indicating how the variables \(V\) and \(T\) are connected at all times.
In this case, \(T=a+bV\), where \(a\) is the \(y-\)intercept and \(b\) is the slope. You should be able to prove that the values of \(a\) and \(b\) for this path are:
\[ \begin{align*} a&=T_i-\dfrac{T_f-T_i}{V_f-V_i}V_i \\[4pt] b&=\dfrac{T_f-T_i}{V_f-V_i} \end{align*} \nonumber\]
Because \(T=a+bV\), \(dT=bdV\), \(V=(T-a)/b\), and \(dV=dT/b\). These relationships tell us how \(T\) and \(V\) are connected throughout the path, and we can therefore write these equivalent expressions:
\[\int\limits_{path}\left(-\dfrac{RT}{V^2}dV+\dfrac{R}{V} dT\right)=-\int_{V_i}^{V_f}\left(-\dfrac{R(a+bV)}{V^2}dV\right)+\int_{T_i}^{T_f}\left(\dfrac{bR}{T-a} dT\right) \nonumber\]
\[\int\limits_{path}\left(-\dfrac{RT}{V^2}dV+\dfrac{R}{V} dT\right)=-\int_{V_i}^{V_f}\left(-\dfrac{R(a+bV)}{V^2}dV\right)+\int_{V_i}^{V_f}\left(\dfrac{R}{V} bdV\right) \nonumber\]
\[\int\limits_{path}\left(-\dfrac{RT}{V^2}dV+\dfrac{R}{V} dT\right)=-\int_{T_i}^{T_f}\left(-\dfrac{RT}{\left[(T-a)/b\right]^2}\dfrac{1}{b}dT\right)+\int_{T_i}^{T_f}\left(\dfrac{bR}{T-a} \right)dT \nonumber\]
In the first case we just wrote the first integrand in terms of \(V\) only and the second integrand in terms of \(T\) only. To achieve this, we used the information from the path to see how \(V\) and \(T\) are related as we move from our initial to our final states. The same idea applies to the second and third lines, where we wrote everything in terms of \(V\) or in terms of \(T\). The three equations will give the same result regardless of whether the differential is exact on inexact. However, because we are integrating an exact differential, the result will be identical to the result we got for the two other paths that share the same initial and final state, and also identical to \(P_f-P_i\).
The three equations above are not too hard to solve, but they are more time consuming that the integrals we had to solve for the paths involving sections of the path where one or the other variable remain constant. This is powerful, because it means that if you are integrating an exact differential, you can get smart and solve the integral for a very easy path, as long as the initial and final states are the same. You know the result will be the same because the differential is exact. If, on the other hand, the differential is inexact, we are out of luck. The integral depends on the path, so we need to solve the path we are given.
Because \(dP\) is exact, the line integral equals \(P_f-P_i\). A consequence of this is that the integral along a closed path (one where \(P_i=P_f\)) is zero. Mathematically:
\[\oint dP=0 \nonumber\]
where the circle inside the integration symbol means that the path is closed. This is true for any exact differential, but not necessarily true for a differential that is inexact. Coming back to thermodynamics, imagine one mole of a gas in a container whose volume is first reduced from 30 L to 20 L at a constant temperature T= 250 K. You then heat the gas up to 300 K keeping the volume constant, then increase the volume back to 30 L keeping the temperature constant, and finally cool it down to 250 K at constant volume (see Figure \(\PageIndex{1}\). Because the initial and final states are the same, the line integral of any state function is zero:
\[\Delta P=\oint dP=0 \nonumber\]
\[\Delta G= \oint dG= 0 \nonumber\]
\[\Delta S =\oint dS=0 \nonumber\]
etc, etc
This closed path does not involve a change in pressure, free energy or entropy, because these functions are state functions, and the final state is identical to the initial state.
On the other hand,
\[w=\oint dw\neq0 \nonumber\]
\[q= \oint dq\neq 0 \nonumber\]
because we are integrating inexact differentials. Physically, you had to do work to expand the gas, heat it up, compress it, cool it down, etc. It does not matter you end up exactly where you started, work and heat were involved in the process. It may be possible for a particular closed path to yield \(w=0\) or \(q=0\), but in general this does not need to be the case.
Given the following differential \(dz=x\;dy+2y\;dx\), and the closed path shown in the figure, calculate the line integral \(\int\limits_{path}dz\)
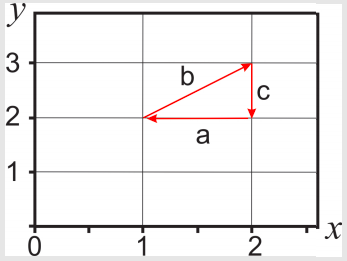
Note: This problem is also available in video format: http://tinyurl.com/mszuwr7
Solution
The path is divided in three sections, so
\[\int\limits_{path}dz= \int_{a}dz+ \int_{b}dz+ \int_{c}dz \nonumber\]
In section \(a\): \(y=2\), \(dy=0\) (\(y\) is a constant), and \(x\) changes from an initial value of 2 to a final value of 1:
\[\int_{a}dz=\int_{2}^1 4 dx=4x\left. \right|_{2}^1=4-8=-4 \nonumber\]
In section \(b\): \(y=1+x\), \(dy=dx\), and \(x\) changes from an initial value of 1 to a final value of 2:
\[\int_{b}dz=\int_{b}x\;dy+2y\;dx=\int_{1}^{2} x\; dx+\int_{1}^2 2(1+x) \;dx=\left.\dfrac{x^2}{2}\right|_{1}^{2}+2\left.\dfrac{(1+x)^2}{2}\right|_{1}^{2}=\dfrac{3}{2}+(9-4)=\dfrac{13}{2} \nonumber\]
In section \(c\): \(x=2\), \(dx=0\) (\(x\) is a constant), and \(y\) changes from an initial value of 3 to a final value of 2:
\[\int_{c}dz=\int_{3}^2 2 dy=2y\left. \right|_{3}^2=4-6=-2 \nonumber\]
Therefore,
\[\int\limits_{path}dz= \int_{a}dz+ \int_{b}dz+ \int_{c}dz=-4+13/2-2=\displaystyle{\color{Maroon}1/2} \nonumber\]
Notice that the integral is not zero even if the path was closed. This is not surprising given that the differential was inexact.
Consider the differential
\[du=(x^2-y^2)dx+(2xy)dy \nonumber\]
- Is \(du\) exact or inexact?
- Explain why each of the following is true or false:
- \(du\) is the total differential of some function \(u(x,y)\). Find \(u(x,y)\) if possible.
- \(\int_{a}du= \int_{b}du= \int_{c}du\) as long as \(a,b\) and \(c\) are paths in the \((x,y)\) space that share the same starting and ending points.
- Calculate \(\int\limits_{path}du\) if the path is the straight line joining the points (0,2) and (2,0).
Solution:
To test whether \(du\) is exact or inexact, we compare the following derivatives
\[\left(\dfrac{\partial (x^2-y^2)}{\partial y} \right )_x\overset{?}{=}\left(\dfrac{\partial (2xy)}{\partial x} \right )_y \nonumber \]
Because the two partial derivatives are not the same, the differential is inexact.
Because the differential is inexact, it is not the total differential of a function \(u(x,y)\). We cannot find the function because it does not exist.
The line integrals \(\int_{a}du, \int_{b}du\) and \(\int_{c}du\) will in principle be different because the integral of an inexact differential depends not only on the initial and final states, but also on the path used to get from the initial to the final state. The statement would be true for an exact differential.
To calculate the integral along the straight line joining the points (0,2) and (2,0), we first need to find the equation \(y(x)\) that describes this path. Sketching the function is not a must, but it might help:
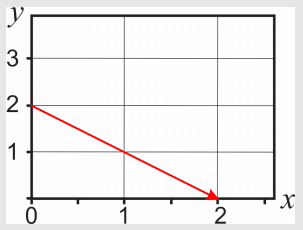
The equation of this straight line is \(y=2-x\). Therefore, along the path, \(y=2-x\) and \(dy=-dx\). The variable \(x\) changes from an initial value \(x=0\) to a final value \(x=2\):
\[\int\limits_{path}du=\int\limits_{path}(x^2-y^2)dx+(2xy)dy \nonumber\]
It is important to stress that \(x\) and \(y\) are not independent along the process, but instead, they are connected through the equation of the path. We will write the equation in terms of \(x\) (we could do it in terms of \(y\) with identical results):
\[ \begin{align*} \int\limits_{path}du &=\int\limits_{path}(x^2-y^2)dx+(2xy)dy \\[4pt] &=\int_{0}^2(x^2-(2-x)^2)dx+\int_{0}^2(2x(2-x))(-dx) \\[4pt] &=\int_{0}^2(x^2-(4+x^2-4x))dx-\int_{0}^2(4x-2x^2)dx \\[4pt] &=\int_{0}^2(4x-4)dx-\int_{0}^2(4x-2x^2)dx=\int_{0}^2(2x^2-4)dx \\[4pt] &=\left. \left(\dfrac{2x^3}{3}-4x\right)\right|_{0}^{2}=\dfrac{16}{3}-8=-\dfrac{8}{3} \\[4pt] &=\displaystyle{\color{Maroon}-\dfrac{8}{3}} \end{align*} \nonumber\]


