3.1: Maclaurin Series
- Page ID
- 106813
A function \(f(x)\) can be expressed as a series in powers of \(x\) as long as \(f(x)\) and all its derivatives are finite at \(x=0\). For example, we will prove shortly that the function \(f(x) = \dfrac{1}{1-x}\) can be expressed as the following infinite sum:
\[\label{eq1}\dfrac{1}{1-x}=1+x+x^2+x^3+x^4 + \ldots\]
We can write this statement in this more elegant way:
\[\label{eq2}\dfrac{1}{1-x}=\displaystyle\sum_{n=0}^{\infty} x^{n}\]
If you are not familiar with this notation, the right side of the equation reads “sum from \(n=0\) to \(n=\infty\) of \(x^n.\)” When \(n=0\), \(x^n = 1\), when \(n=1\), \(x^n = x\), when \(n=2\), \(x^n = x^2\), etc (compare with Equation \ref{eq1}). The term “series in powers of \(x\)” means a sum in which each summand is a power of the variable \(x\). Note that the number 1 is a power of \(x\) as well (\(x^0=1\)). Also, note that both Equations \ref{eq1} and \ref{eq2} are exact, they are not approximations.
Similarly, we will see shortly that the function \(e^x\) can be expressed as another infinite sum in powers of \(x\) (i.e. a Maclaurin series) as:
\[\label{expfunction}e^x=1+x+\dfrac{1}{2} x^2+\dfrac{1}{6}x^3+\dfrac{1}{24}x^4 + \ldots \]
Or, more elegantly:
\[\label{expfunction2}e^x=\displaystyle\sum_{n=0}^{\infty}\dfrac{1}{n!} x^{n}\]
where \(n!\) is read “n factorial” and represents the product \(1\times 2\times 3...\times n\). If you are not familiar with factorials, be sure you understand why \(4! = 24\). Also, remember that by definition \(0! = 1\), not zero.
At this point you should have two questions: 1) how do I construct the Maclaurin series of a given function, and 2) why on earth would I want to do this if \(\dfrac{1}{1-x}\) and \(e^x\) are fine-looking functions as they are. The answer to the first question is easy, and although you should know this from your calculus classes we will review it again in a moment. The answer to the second question is trickier, and it is what most students find confusing about this topic. We will discuss different examples that aim to show a variety of situations in which expressing functions in this way is helpful.
How to obtain the Maclaurin Series of a Function
In general, a well-behaved function (\(f(x)\) and all its derivatives are finite at \(x=0\)) will be expressed as an infinite sum of powers of \(x\) like this:
\[\label{eq3}f(x)=\displaystyle\sum_{n=0}^{\infty}a_n x^{n}=a_0+a_1 x + a_2 x^2 + \ldots + a_n x^n\]
Be sure you understand why the two expressions in Equation \ref{eq3} are identical ways of expressing an infinite sum. The terms \(a_n\) are called the coefficients, and are constants (that is, they are NOT functions of \(x\)). If you end up with the variable \(x\) in one of your coefficients go back and check what you did wrong! For example, in the case of \(e^x\) (Equation \ref{expfunction}), \(a_0 =1, a_1=1, a_2 = 1/2, a_3=1/6, etc\). In the example of Equation \ref{eq1}, all the coefficients equal 1. We just saw that two very different functions can be expressed using the same set of functions (the powers of \(x\)). What makes \(\dfrac{1}{1-x}\) different from \(e^x\) are the coefficients \(a_n\). As we will see shortly, the coefficients can be negative, positive, or zero.
How do we calculate the coefficients? Each coefficient is calculated as:
\[\label{series:coefficients}a_n=\dfrac{1}{n!} \left( \dfrac{d^n f(x)}{dx^n} \right)_0\]
That is, the \(n\)-th coefficient equals one over the factorial of \(n\) multiplied by the \(n\)-th derivative of the function \(f(x)\) evaluated at zero. For example, if we want to calculate \(a_2\) for the function \(f(x)=\dfrac{1}{1-x}\), we need to get the second derivative of \(f(x)\), evaluate it at \(x=0\), and divide the result by \(2!\). Do it yourself and verify that \(a_2=1\). In the case of \(a_0\) we need the zeroth-order derivative, which equals the function itself (that is, \(a_0 = f(0)\), because \(\dfrac{1}{0!}=1\)). It is important to stress that although the derivatives are usually functions of \(x\), the coefficients are constants because they are expressed in terms of the derivatives evaluated at \(x=0\).
Note that in order to obtain a Maclaurin series we evaluate the function and its derivatives at \(x=0\). This procedure is also called the expansion of the function around (or about) zero. We can expand functions around other numbers, and these series are called Taylor series (see Section 3).
Obtain the Maclaurin series of \(sin(x)\).
Solution
We need to obtain all the coefficients (\(a_0, a_1...etc\)). Because there are infinitely many coefficients, we will calculate a few and we will find a general pattern to express the rest. We will need several derivatives of \(sin(x)\), so let’s make a table:
| \(n\) | \(\dfrac{d^n f(x)}{dx^n}\) | \(\left( \dfrac{d^n f(x)}{dx^n} \right)_0\) |
|---|---|---|
| 0 | \(\sin (x)\) | 0 |
| 1 | \(\cos (x)\) | 1 |
| 2 | \(-\sin (x)\) | 0 |
| 3 | \(-\cos (x)\) | -1 |
| 4 | \(\sin (x)\) | 0 |
| 5 | \(\cos (x)\) | 1 |
Remember that each coefficient equals \(\left( \dfrac{d^n f(x)}{dx^n} \right)_0\) divided by \(n!\), therefore:
| \(n\) | \(n!\) | \(a_n\) |
|---|---|---|
| 0 | 1 | 0 |
| 1 | 1 | 1 |
| 2 | 2 | 0 |
| 3 | \(6\) | \(-\dfrac{1}{6}\) |
| 4 | \(24\) | 0 |
| 5 | \(120\) | \(\dfrac{1}{120}\) |
This is enough information to see the pattern (you can go to higher values of \(n\) if you don’t see it yet):
- the coefficients for even values of \(n\) equal zero.
- the coefficients for \(n = 1, 5, 9, 13,...\) equal \(1/n!\)
- the coefficients for \(n = 3, 7, 11, 15,...\) equal \(-1/n!\).
Recall that the general expression for a Maclaurin series is \(a_0+a_1 x + a_2 x^2...a_n x^n\), and replace \(a_0...a_n\) by the coefficients we just found:
\[\displaystyle{\color{Maroon}\sin (x) = x - \dfrac{1}{3!} x^3+ \dfrac{1}{5!} x^5 -\dfrac{1}{7!} x^7...} \nonumber\]
This is a correct way of writing the series, but in the next example we will see how to write it more elegantly as a sum.
Express the Maclaurin series of \(\sin (x)\) as a sum.
Solution
In the previous example we found that:
\[\label{series:sin}\sin (x) = x - \dfrac{1}{3!} x^3+ \dfrac{1}{5!} x^5 -\dfrac{1}{7!} x^7...\]
We want to express this as a sum:
\[\displaystyle\sum_{n=0}^{\infty}a_n x^{n} \nonumber\]
The key here is to express the coefficients \(a_n\) in terms of \(n\). We just concluded that 1) the coefficients for even values of \(n\) equal zero, 2) the coefficients for \(n = 1, 5, 9, 13,...\) equal \(1/n!\) and 3) the coefficients for \(n = 3, 7, 11,...\) equal \(-1/n!\). How do we put all this information together in a unique expression? Here are three possible (and equally good) answers:
- \(\displaystyle{\color{Maroon}\sin (x)=\displaystyle\sum_{n=0}^{\infty} \left( -1 \right) ^n \dfrac{1}{(2n+1)!} x^{2n+1}}\)
- \(\displaystyle{\color{Maroon}\sin (x)=\displaystyle\sum_{n=1}^{\infty} \left( -1 \right) ^{(n+1)} \dfrac{1}{(2n-1)!} x^{2n-1}}\)
- \(\displaystyle{\color{Maroon}\sin (x)=\displaystyle\sum_{n=0}^{\infty} cos(n \pi) \dfrac{1}{(2n+1)!} x^{2n+1}}\)
This may look impossibly hard to figure out, but let me share a few tricks with you. First, we notice that the sign in Equation \ref{series:sin} alternates, starting with a “+”. A mathematical way of doing this is with a term \((-1)^n\) if your sum starts with \(n=0\), or \((-1)^{(n+1)}\) if you sum starts with \(n=1\). Note that \(\cos (n \pi)\) does the same trick.
| \(n\) | \((-1)^n\) | \((-1)^{n+1}\) | \(\cos (n \pi)\) |
|---|---|---|---|
| 0 | 1 | -1 | 1 |
| 1 | -1 | 1 | -1 |
| 2 | 1 | -1 | 1 |
| 3 | -1 | 1 | -1 |
We have the correct sign for each term, but we need to generate the numbers \(1, \dfrac{1}{3!}, \dfrac{1}{5!}, \dfrac{1}{7!},...\) Notice that the number “1” can be expressed as \(\dfrac{1}{1!}\). To do this, we introduce the second trick of the day: we will use the expression \(2n+1\) to generate odd numbers (if you start your sum with \(n=0\)) or \(2n-1\) (if you start at \(n=1\)). Therefore, the expression \(\dfrac{1}{(2n+1)!}\) gives \(1, \dfrac{1}{3!}, \dfrac{1}{5!}, \dfrac{1}{7!},...\), which is what we need in the first and third examples (when the sum starts at zero).
Lastly, we need to use only odd powers of \(x\). The expression \(x^{(2n+1)}\) generates the terms \(x, x^3, x^5...\) when you start at \(n=0\), and \(x^{(2n-1)}\) achieves the same when you start your series at \(n=1\).
Confused about writing sums using the sum operator \((\sum)\)? This video will help: http://tinyurl.com/lvwd36q
Need help? The links below contain solved examples.
External links:
Finding the maclaurin series of a function I: http://patrickjmt.com/taylor-and-maclaurin-series-example-1/
Finding the maclaurin series of a function II: http://www.youtube.com/watch?v= dp2ovDuWhro
Finding the maclaurin series of a function III: http://www.youtube.com/watch?v= WWe7pZjc4s8
Graphical Representation
From Equation \(\ref{eq3}\) and the examples we discussed above, it should be clear at this point that any function whose derivatives are finite at \(x=0\) can be expressed by using the same set of functions: the powers of \(x\). We will call these functions the basis set. A basis set is a collection of linearly independent functions that can represent other functions when used in a linear combination.
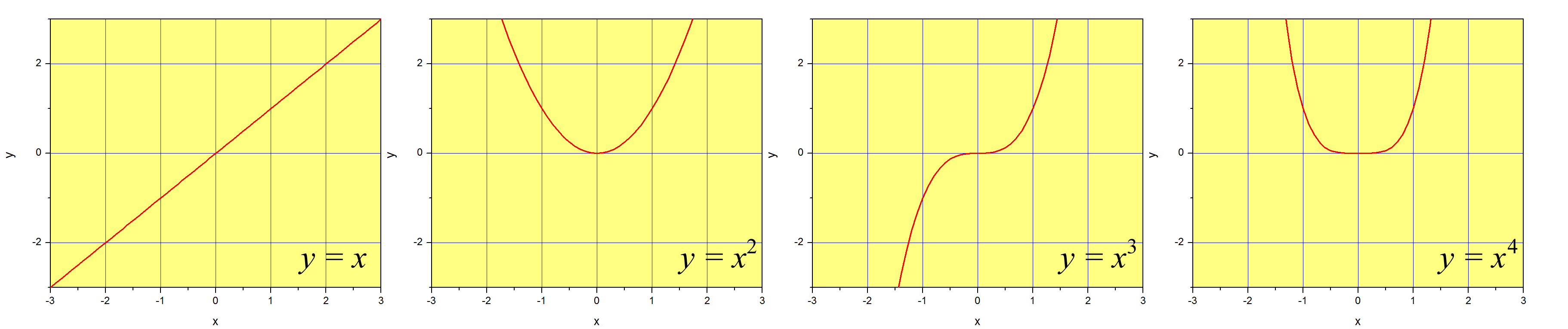
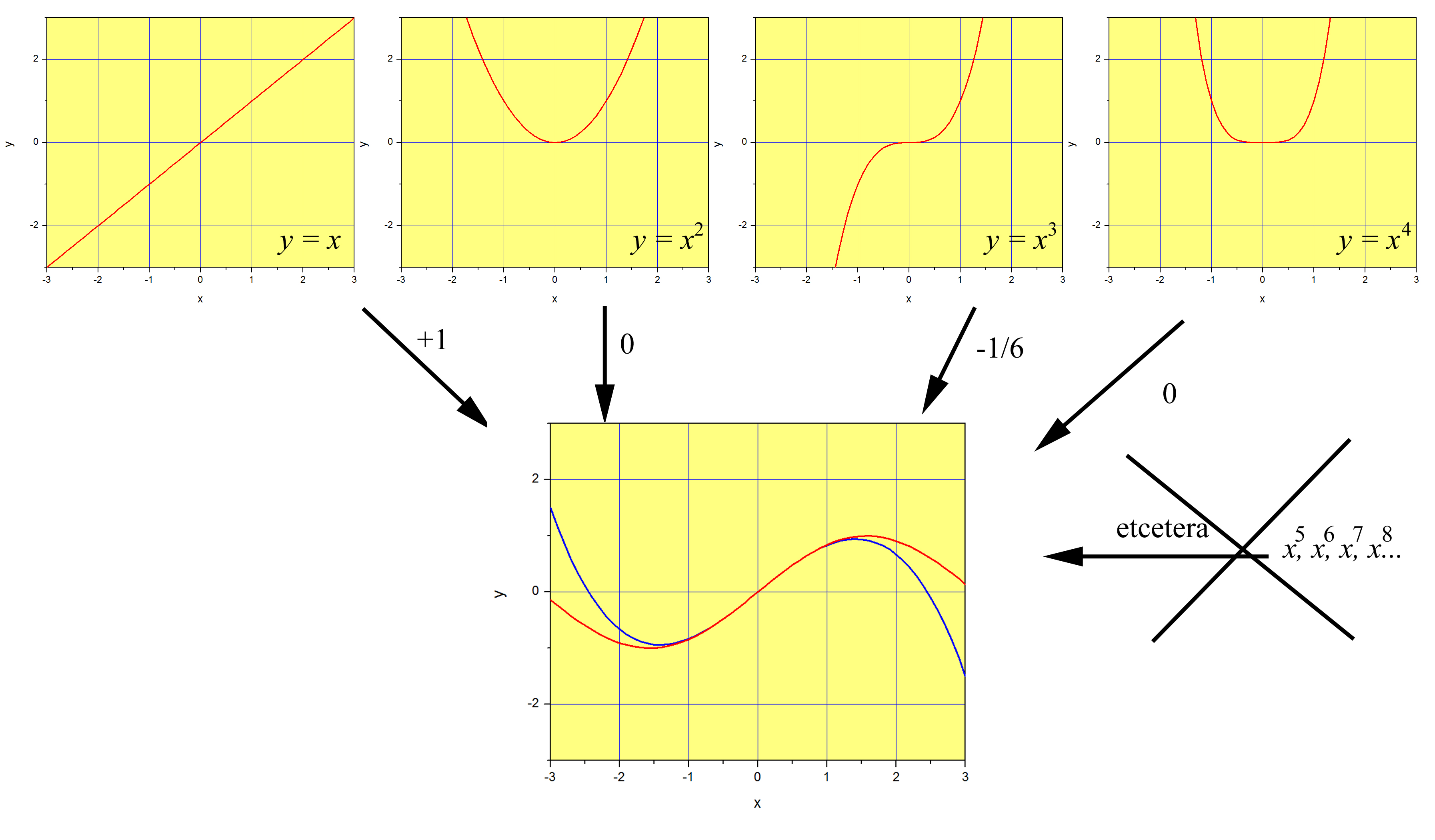
Figure \(\PageIndex{1}\) is a graphic representation of the first four functions of this basis set. To be fair, the first function of the set is \(x^0=1\), so these would be the second, third, fourth and fifth. The full basis set is of course infinite in length. If we mix all the functions of the set with equal weights (we put the same amount of \(x^2\) than we put \(x^{245}\) or \(x^{0}\)), we obtain \((1-x)^{-1}\) (Equation \ref{eq1}. If we use only the odd terms, alternate the sign starting with a ‘+’, and weigh each term less and less using the expression \(1/(2n-1)!\) for the \(n-th\) term, we obtain \(\sin{x}\) (Equation \ref{series:sin}). This is illustrated in Figure \(\PageIndex{2}\), where we multiply the even powers of \(x\) by zero, and use different weights for the rest. Note that the ‘etcetera’ is crucial, as we would need to include an infinite number of functions to obtain the function \(\sin{x}\) exactly.

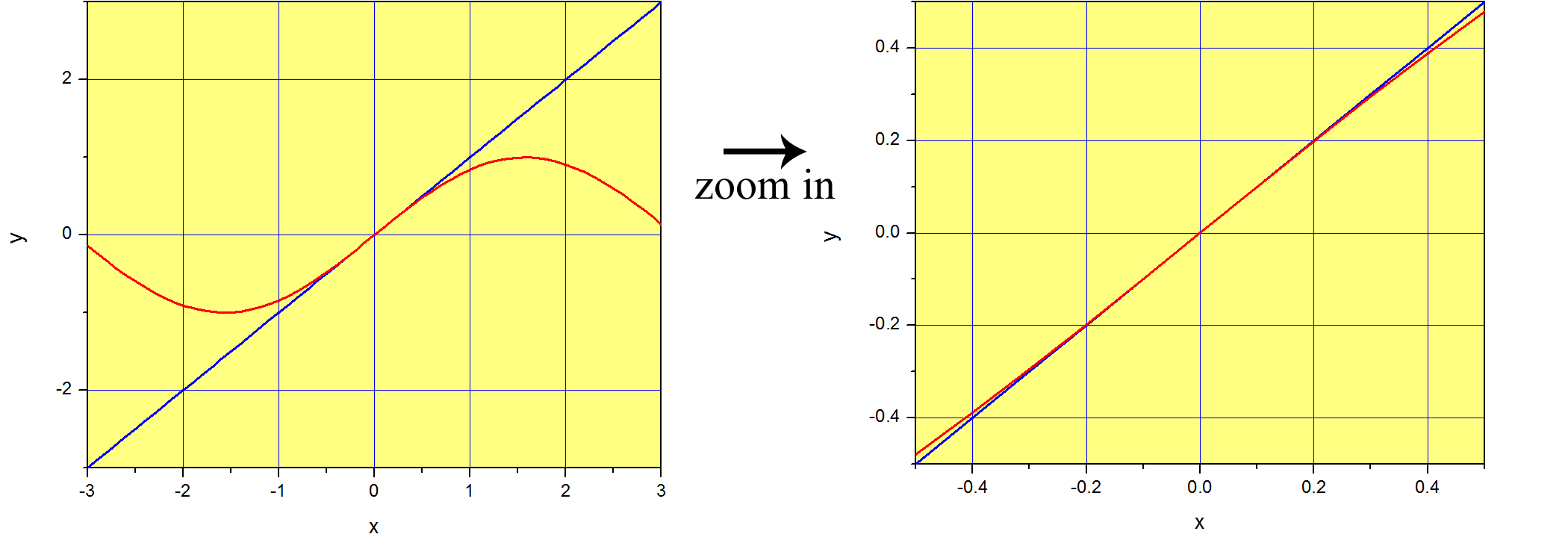
Although we need an infinite number of terms to express a function exactly (unless the function is a polynomial, of course), in many cases we will observe that the weight (the coefficient) of each power of \(x\) gets smaller and smaller as we increase the power. For example, in the case of \(\sin{x}\), the contribution of \(x^3\) is \(1/6 th\) of the contribution of \(x\) (in absolute terms), and the contribution of \(x^5\) is \(1/120 th\). This tells you that the first terms are much more important than the rest, although all are needed if we want the sum to represent \(\sin{x}\) exactly. What if we are happy with a ‘pretty good’ approximation of \(\sin{x}\)? Let’s see what happens if we use up to \(x^3\) and drop the higher terms. The result is plotted in blue in Figure \(\PageIndex{3}\) together with \(\sin{x}\) in red. We can see that the function \(x-1/6 x^3\) is a very good approximation of \(\sin{x}\) as long as we stay close to \(x=0\). As we move further away from the origin the approximation gets worse and worse, and we would need to include higher powers of \(x\) to get it better. This should be clear from eq. [series:sin], since the terms \(x^n\) get smaller and smaller with increasing \(n\) if \(x\) is a small number. Therefore, if \(x\) is small, we could write \(\sin (x) \approx x - \dfrac{1}{3!} x^3\), where the symbol \(\approx\) means approximately equal.
But why stopping at \(n=3\) and not \(n=1\) or 5? The above argument suggests that the function \(x\) might be a good approximation of \(\sin{x}\) around \(x=0\), when the term \(x^3\) is much smaller than the term \(x\). This is in fact this is the case, as shown in Figure \(\PageIndex{4}\).
We have seen that we can get good approximations of a function by truncating the series (i.e. not using the infinite terms). Students usually get frustrated and want to know how many terms are ‘correct’. It takes a little bit of practice to realize there is no universal answer to this question. We would need some context to analyze how good of an approximation we are happy with. For example, are we satisfied with the small error we see at \(x= 0.5\) in Figure \(\PageIndex{4}\)? It all depends on the context. Maybe we are performing experiments where we have other sources of error that are much worse than this, so using an extra term will not improve the overall situation anyway. Maybe we are performing very precise experiments where this difference is significant. As you see, discussing how many terms are needed in an approximation out of context is not very useful. We will discuss this particular approximation when we learn about second order differential equations and analyze the problem of the pendulum, so hopefully things will make more sense then.