1.2: Odd and Even Functions
- Page ID
- 106799
Many of you probably heard about odd and even functions in previous courses, but for those who did not, here is a brief introduction.
- An odd function obeys the relation \(f(x) = −f(−x)\). For example, \(\sin x\) is odd because \(\sin x = − \sin(−x)\).
- An even function obeys the relation \(f(x) = f(−x)\). For example, \(\cos x\) is even because \(\cos x = \cos(−x)\).
Even functions are symmetric with respect to the y−axis. In other words, if you were to put a mirror perpendicular to the screen at \(x = 0\), the right side of the plot would produce a reflection that would overlap with the left side of the plot. Check Figure \(\PageIndex{1}\) to be sure you understand what this means.

Odd functions are symmetric in a different way. Imagine that you have an axis perpendicular to the screen that contains the point (0,0). Now rotate every point of your graph 180 degrees. If the plot you create after rotation overlaps with the plot before the rotation, the function is odd. Check Figure \(\PageIndex{1}\) to be sure you understand what this means.
Note that functions do not necessarily need to be even or odd. The function \(e^x\), for instance, is clearly neither, as \(e^x \neq e^{−x}\) (condition for even) and \(e^x \neq −e^{−x}\) (condition for odd). You can also sketch the function \(e^x\) and verify that it does not have the symmetry of an odd or even function. For any function,
\[ \int_{-a}^a f(x)dx = \int_{-a}^0 f(x) dx + \int_0^{a} f(x) dx\]
For an odd function, this integral equals zero:
\[ \label{eq2} \int_{-a}^a f(x)dx = \int_{-a}^0 f(x) dx + \int_0^{a} f(x) dx = 0\]
This should be obvious just by looking at the plot of \(\sin x\). The area under the curve between 0 and \(a\) cancels out with the area under the curve between \(−a\) and 0. This is great news because it means that we do not have to bother integrating odd functions as long as the limits of integration span from \(−a\) to \(a\), where a can be any number, including infinity. As it turns out this happens often in quantum mechanics, so it is something worth keeping in mind!
For an even function,
\[ \int_{-a}^a f(x)dx = 2 \int_{0}^{a} f(x) dx\]
because the area under the curve between 0 and \(a\) equals the area under the curve between \(−a\) and 0. This not as helpful as Equation \ref{eq2}, but still might help in some cases. For example, let’s say that you need to evaluate \(\int_{- \infty}^{\infty} x^2 e^{-x^2} dx\) and the only material that you have available is the formula sheet. You find an expression for
\[\int_0^{\infty} x^{2n} e^{-ax^2} dx \nonumber\]
which you can use with \(n = 1\) to obtain
\[\int_0^{\infty} x^2 e^{−x^2} dx = \frac{ \sqrt{\pi}}{4} \nonumber\] (be sure you can get this result on your own).
How do you get \(\int_{- \infty}^{\infty} x^2 e^{-x^2} dx\)? If the integrand is even, you just need to multiply by 2. This is in fact an even function, because \(x^2 = (−x)^2\), and therefore it is clear that \(x^2 e^{−x^2} = (−x)^2 e^{−(−x)^2}\). Therefore,
\[\int_{- \infty}^{\infty} x^2 e^{-x^2} dx = \frac{\sqrt{\pi}}{2} \nonumber\]
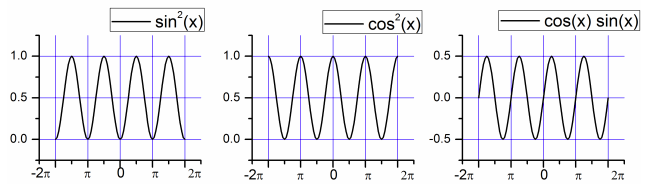
It is useful to know that the product of two even functions or two odd functions is an even function, and the product of an odd function and an even function is odd. For example,
- \(\sin^2 x\) is the product of two odd functions, and is therefore even.
- \(\cos^2 x\) is the product of two even functions, and is therefore even.
- \(\sin x \cos x\) is the product of an odd function and an even function, and is therefore odd.
Need help understanding how to identify odd and even functions? External links:


