6.1: Theoretical Treatment of Electronic Structure
- Page ID
- 11589
In Chapter 5, I introduced you to the strategies that theory uses to interpret experimental data relating to such matters, and how and why theory can also be used to simulate the behavior of molecules. In carrying out simulations, the Born-Oppenheimer electronic energy \(E(R)\) as a function of the \(3N\) coordinates of the \(N\) atoms in the molecule plays a central role. It is on this landscape that one searches for stable isomers and transition states, and it is the second derivative (Hessian) matrix of this function that provides the harmonic vibrational frequencies of such isomers. In the present Chapter, I want to provide you with an introduction to the tools that we use to solve the electronic Schrödinger equation to generate \(E(R)\) and the electronic wave function \(\psi(r|R)\). In essence, this treatment will focus on orbitals of atoms and molecules and how we obtain and interpret them.
For an atom, one can approximate the orbitals by using the solutions of the hydrogenic Schrödinger equation discussed in Part 1 of this text. Although such functions are not proper solutions to the actual \(N\)-electron Schrödinger equation (believe it or not, no one has ever solved exactly any such equation for \(N > 1\)) of any atom, they can be used as perturbation or variational starting-point approximations when one may be satisfied with qualitatively accurate answers. In particular, the solutions of this one-electron hydrogenic problem form the qualitative basis for much of atomic and molecular orbital theory. As discussed in detail in Part 1, these orbitals are labeled by \(n\), \(l\), and \(m\) quantum numbers for the bound states and by \(l\) and \(m\) quantum numbers and the energy \(E\) for the continuum states.
Much as the particle-in-a-box orbitals are used to qualitatively describe \(\pi\)-electrons in conjugated polyenes or electronic bands in solids, these so-called hydrogen-like orbitals provide qualitative descriptions of orbitals of atoms with more than a single electron. By introducing the concept of screening as a way to represent the repulsive interactions among the electrons of an atom, an effective nuclear charge \(Z_{\rm eff}\) can be used in place of \(Z\) in the hydrogenic \(\psi_{n,l,m}\) and \(E_{n,l}\) formulas to generate approximate atomic orbitals to be filled by electrons in a many-electron atom. For example, in the crudest approximation of a carbon atom, the two \(1s\) electrons experience the full nuclear attraction so \(Z_{\rm eff} =6\) for them, whereas the \(2s\) and \(2p\) electrons are screened by the two \(1s\) electrons, so \(Z_{\rm eff}= 4\) for them. Within this approximation, one then occupies two \(1s\) orbitals with \(Z=6\), two \(2s\) orbitals with \(Z=4\) and two \(2p\) orbitals with \(Z=4\) in forming the full six-electron product wave function of the lowest-energy state of carbon
\[\psi(1, 2, …, 6) = \psi_{1s} \alpha(1) \psi_{1s} \alpha(2) \psi_{2s} \alpha(3) … \psi_{1p}(0) \beta(6). \]
However, such approximate orbitals are not sufficiently accurate to be of use in quantitative simulations of atomic and molecular structure. In particular, their energies do not properly follow the trends in atomic orbital (AO) energies that are taught in introductory chemistry classes and that are shown pictorially in Figure 6.1.
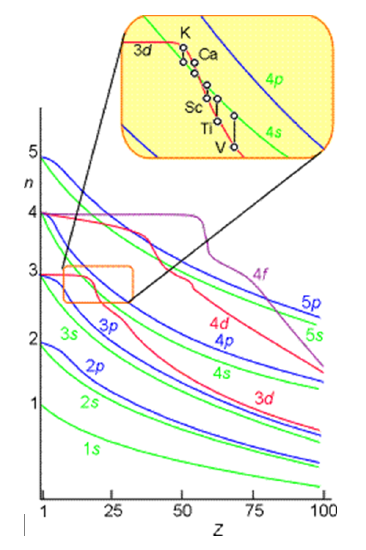
For example, the relative energies of the \(3d\) and \(4s\) orbitals are not adequately described in a model that treats electron repulsion effects in terms of a simple screening factor. So, now it is time to examine how we can move beyond the screening model and take the electron repulsion effects, which cause the inter-electronic couplings that render the Schrödinger equation insoluble, into account in a more reliable manner.
Atomic Units
The electronic Hamiltonian that appears throughout this text is commonly expressed in the literature and in other texts in so-called atomic units (aus). In that form, it is written as follows:
\[H_e = \sum_j \left[ -\frac{1}{2} \nabla_j^2 - \sum_a \frac{Z_a}{r_{j,a}} \right] + \sum_{j< k} \frac{1}{r_{j,k}} .\]
Atomic units are introduced to remove all of the h , e, and me factors from the Schrödinger equation.
To effect the unit transformation that results in the Hamiltonian appearing as above, one notes that the kinetic energy operator scales as \(r_j^{-2}\) whereas the Coulomb potentials scale as \(r_j^{-1}\) and as \(r_{j,k}^{-1}\). So, if each of the Cartesian coordinates of the electrons and nuclei were expressed as a unit of length \(a_0\) multiplied by a dimensionless length factor, the kinetic energy operator would involve terms of the form
\(( - \hbar^2/2(a_0)^2m_e ) \nabla_j^2\), and the Coulomb potentials would appear as \(Z_ae^2/(a_0)r_{j,a}\) and \(e^2/(a_0)r_{j,k}\), with the \(r_{j,a}\) and \(r_{j,k}\) factors now referring to the dimensionless coordinates. A factor of \(e^2/a_0\) (which has units of energy since a_0 has units of length) can then be removed from the Coulomb and kinetic energies, after which the kinetic energy terms appear as \(( - \hbar^2/2(e^2a_0)m_e ) \nabla_j^2\) and the potential energies appear as \(Z_a/r_{j,a}\) and \(1/r_{j,k}\). Then, choosing \(a_0 = \hbar^2/e^2m_e\) changes the kinetic energy terms into \(-1/2 \nabla_j^2\); as a result, the entire electronic Hamiltonian takes the form given above in which no \(e^2\), me, or \(\hbar^2\) factors appear. The value of the so-called Bohr radius \(a_0 = \hbar^2/e^2m_e\) turns out to be 0.529 Å, and the so-called Hartree energy unit \(e^2/a_0\), which factors out of He, is 27.21 eV or 627.51 kcal/mol.
Contributors and Attributions
Jack Simons (Henry Eyring Scientist and Professor of Chemistry, U. Utah) Telluride Schools on Theoretical Chemistry
Integrated by Tomoyuki Hayashi (UC Davis)


