3.E: Exercises
- Page ID
- 64674
Q1
In 1913 Niels Bohr proposed a model for the hydrogen atom which gives the correct expression for the energy levels En. His model was based on an awkward marriage of classical mechanics and, at that time, the new idea of quantization. In the Bohr model of the hydrogen atom the electron is assumed to move in a circular orbit around the nucleus, as illustrated in Fig. 3-7. The energy of the electron in such an orbit is: (1)
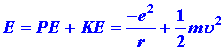
where u is the tangential velocity of the electron in the orbit. Since the circular orbit is to be a stable one the attractive coulomb force exerted on the electron by the nucleus must be balanced by a centrifugal force, or: (2)
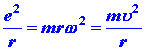
where w is the circular velocity of the electron. Up until this point the model is completely classical in concept. However, Bohr now postulated that only those orbits are allowed for which the angular momentum is an integral multiple of (h/2p). In other words, Bohr postulated that the angular momentum of the electron in the hydrogen atom is quantized. This postulate gives a further equation: (3)
- Show that by eliminating r and u from these three equations you can obtain the correct expression for En.
- Show that Bohr's model correctly predicts that the KE = -½PE.
- Show that the radius of the first Bohr orbit is identical to the maximum value of r for the n = 1 level of the hydrogen atom,
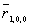 , as calculated by quantum mechanics.
, as calculated by quantum mechanics. - Criticize the Bohr model in the light of the quantum mechanical results for the hydrogen atom.
Q2
The part of the hydrogen atom spectrum which occurs in the visible region arises from electrons in excited levels falling to the n = 2 level. The quantum mechanical expression for the frequencies in this case, corresponding to equation (3) of the text for the Lyman series, is: (4)
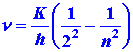
The energy of an emitted photon for a jump from level n to level 2 is: (5)
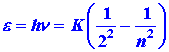
Equation (5) predicts that a plot of the photon energies versus (1/n2) should be a straight line. Furthermore, it predicts that the intercept of this line with the energy axis, corresponding to the value of 1/n2 = 0, i.e., n = ¥, should equal (¼)K where: (6)
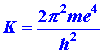
The point of this problem is to test these theoretical predictions against the experimental results.
Experimentally we measure the wavelength of the emitted light by means of a diffraction grating. A grating for the diffraction of visible light may be made by marking a glass plate with parallel, equally spaced lines. There are about 10,000 lines per cm. The spacings between the lines in the grating d is thus about 1 ´10-4 cm which is the order of magnitude of the wavelength of visible light. The diffraction equation is: (7)
as previously discussed in Problem I-1. We measure the angle q for different orders n = 1, 2, 3, ... of the diffracted light beam. Since d is known, l may be calculated. The experimentally measured values for the first four lines in the Balmer series are given below.
Balmer Series
| l(Å) | n |
| 6563 | 3 |
| 4861 | 4 |
| 4341 | 5 |
| 4102 | 6 |
The value of the principal quantum number n which appears in equation (5) is given for each value of l. (This n is totally unrelated to the n of equation (7) for the experimental determination of l.) Calculate the energy of each photon from the value of its wavelength.

Plot the photon energies versus the appropriate value of 1/n2. Let the 1/n2 axis run from 0 to 0.25 and the energy axis run from 0 to 3.6 ev. Include as a point on your graph e = 0 for 1/n2 = 0.25, i.e., when n = 2, the excited level and the level to which the electron falls coincide.
- Do the points fall on a straight line as predicted?
- Determine the value of K by extending the line to intercept the energy axis. This intercept should equal K/4. Read off this value from your graph.
- Compare the experimental value for K with that predicted theoretically by equation (5). Use e = 4.803 ´ 10-10 esu, express m and h in cgs units and the value of K will be in ergs (1 erg = 6.2420 ´ 1011 ev). Recall that K is the ionization potential for the hydrogen atom. An electron falling from the n = ¥ level to the n = 2 level will fall only (¼)K in energy as is evident from the energy level diagram shown in Fig. 3-2.
Q3
A beam of atoms with l = 1 is passed through an atomic beam apparatus with the magnetic field directed along an axis perpendicular to the direc tion of the beam. The undeflected beam from this experiment enters a second beam apparatus in which the magnetic field is directed along an axis which is perpendicular to both the path of the beam and the direction of the field in the first experiment. Will this one component of the original beam be split in the second applied magnetic field? Explain why you think it will be, if this is indeed your answer.

