8.1: Theoretical Tools for Studying Chemical Change and Dynamics
- Page ID
- 11598
Transition State Theory
The most successful and widely employed theoretical approach for studying rates involving species undergoing reaction at or near thermal-equilibrium conditions is the transition state theory (TST) of the author’s late colleague, Henry Eyring. This would not be a good way to model, for example, photochemical reactions in which the reactants do not reach thermal equilibrium before undergoing significant reaction progress. However, for most thermal reactions, it is remarkably successful.
In this theory, one views the reactants as undergoing collisions that act to keep all of their degrees of freedom (translational, rotational, vibrational, electronic) in thermal equilibrium. Among the collection of such reactant molecules, at any instant of time, some will have enough internal energy to access a transition state (TS) on the Born-Oppenheimer potential energy surface upon which the reaction takes place. Within TST, the rate of progress from reactants to products is then expressed in terms of the concentration of species that exist near the TS multiplied by the rate at which these species move through the TS region of the energy surface.
The concentration of species at the TS is, in turn, written in terms of the equilibrium constant expression of statistical mechanics discussed in Chapter 7. For example, for a bimolecular reaction \(A+B \rightarrow C\) passing through a TS denoted AB*, one writes the concentration (in molecules per unit volume) of AB* species in terms of the concentrations of A and of B and the respective partition functions as
\[[AB*] = \dfrac{(q_{AB}^*/V)}{(q_A/V)( q_B/V)} [A] [B].\]
There is, however, one aspect of the partition function of the TS species that is specific to this theory. The partition function \(q_{AB}^*\) contains all of the usual translational, rotational, vibrational, and electronic partition functions that one would write down, as we did in Chapter 7, for a conventional AB molecule except for one modification. It does not contain a
\[\dfrac{\exp(-h\nu_j /2kT)}{1- \exp(-h\nu_j/kT)} \]
vibrational contribution for motion along the one internal coordinate corresponding to the reaction path.
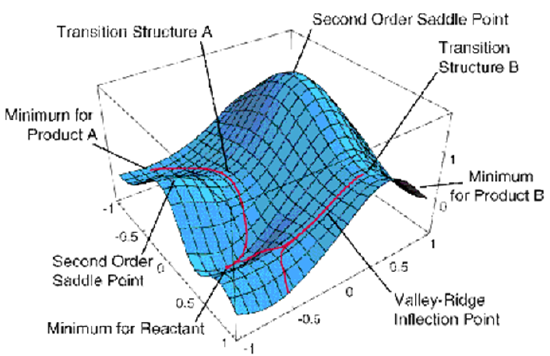
As we discussed in Chapter 3, in the vicinity of the TS, the reaction path can be identified as that direction along which the PES has negative curvature; along all other directions, the energy surface is positively curved. For example, in Figure 8.1, a reaction path begins at Transition Structure B and is directed downhill. More specifically, if one knows the gradients {\((\partial E/\partial q_k)\) }and Hessian matrix elements:
\[H_{j,k} = \dfrac{\partial^2E}{\partial{q_j}\partial{q_k}}\]
of the energy surface at the TS, one can express the variation of the potential energy along the \(3N\) Cartesian coordinates {\(q_k\)} of the molecule as follows:
\[E(q_k) = E(0) + \sum_k \dfrac{\partial E}{\partial q_k} q_k + \dfrac{1}{2} \sum_j^k q_j H_{j,k} q_k + …\]
where E(0) is the energy at the TS, and the {\(q_k\)} denote displacements away from the TS geometry. Of course, at the TS, the gradients all vanish because this geometry corresponds to a stationary point. As we discussed in Chapter 3, the Hessian matrix \(H_{j,k}\) has 6 zero eigenvalues whose eigenvectors correspond to overall translation and rotation of the molecule. This matrix has \(3N-7\) positive eigenvalues whose eigenvectors correspond to the vibrations of the TS species, as well as one negative eigenvalue. The latter has an eigenvector whose components \(\{q_k\}\) along the \(3N\) Cartesian coordinates describe the direction of the reaction path as it begins its journey from the TS backward to reactants (when followed in one direction) and onward to products (when followed in the opposite direction). Once one moves a small amount along the direction of negative curvature, the reaction path is subsequently followed by taking infinitesimal steps downhill along the gradient vector \(\textbf{g}\) whose \(3N\) components are (\(\dfrac{∂E}{∂q_k}\)). Note that once one has moved downhill away from the TS by taking the initial step along the negatively curved direction, the gradient no longer vanishes because one is no longer at the stationary point.
Returning to the TST rate calculation, one therefore is able to express the concentration \([AB^*]\) of species at the TS in terms of the reactant concentrations and a ratio of partition functions. The denominator of this ratio contains the conventional partition functions of the reactant molecules and can be evaluated as discussed in Chapter 7. However, the numerator contains the partition function of the TS species but with one vibrational component missing (i.e.:
\[q_{\rm vib} = \prod_{k=1}^{3N-7} \left[\dfrac{\exp(-h\nu_j /2kT)}{1- \exp(-h\nu_j/kT)}\right].\]
Other than the one missing \(q_{\rm vib}\), the TS's partition function is also evaluated as in Chapter 7. The motion along the reaction path coordinate contributes to the rate expression in terms of the frequency (i.e., how often) with which reacting flux crosses the TS region given that the system is in near-thermal equilibrium at temperature \(T\).
To compute the frequency with which trajectories cross the TS and proceed onward to form products, one imagines the TS as consisting of a narrow region along the reaction coordinate \(s\); the width of this region we denote \(\delta_s\). We next ask what the classical weighting factor is for a collision to have momentum \(p_s\) along the reaction coordinate. Remembering our discussion of such matters in Chapter 7, we know that the momentum factor entering into the classical partition function for translation along the reaction coordinate is \((1/h) \exp(-p_s^2/2\mu kT) dp_s\). Here, m is the mass factor associated with the reaction coordinate s. We can express the rate or frequency at which such trajectories pass through the narrow region of width \(\delta_s\) as \(\dfrac{p_s}{\mu\delta_s}\), with \(\dfrac{p_s}{\mu}\) being the speed of passage (cm s-1) and \(1/\delta_s\) being the inverse of the distance that defines the TS region. So, \(\dfrac{p_s}{\mu\delta_s}\) has units of s-1. In summary, we expect the rate of trajectories moving through the TS region to be
\[\dfrac{1}{h} \exp\Big(\dfrac{-p_s^2}{2\mu kT}\Big) dp_s \dfrac{p_s}{\mu \delta_s}.\]
However, we still need to integrate this over all values of \(p_s\) that correspond to enough energy \(p_s^2/2m\) to access the TS’s energy (relative to that of the reactants), which we denote \(E^*\). Moreover, we have to account for the fact that it may be that not all trajectories with kinetic energy equal to \(E^*\) or greater pass on to form product molecules; some trajectories may pass through the TS but later recross the TS and return to produce reactants. Moreover, it may be that some trajectories with kinetic energy along the reaction coordinate less than \(E^*\) can react by tunneling through the barrier.
The way we account for the fact that a reactive trajectory must have at least \(E^*\) in energy along s is to integrate over only values of \(p_s\) greater than \(\sqrt{2\mu E^*}\). To account for the fact that some trajectories with energies above \(E^*\) may recross, we include a so-called transmission coefficient k whose value is between zero and unity. In the most elementary TST, tunneling is ignored. Putting all of these pieces together, we carry out the integration over \(p_s\) just described to obtain:
\[\int\int \dfrac{\kappa}{h} \exp\Big(\dfrac{-p_s^2}{2\mu kT}\Big) \dfrac{p_s}{\mu\delta_s} \delta_s dp_s\]
where the momentum is integrated from \(p_s = \sqrt{2\mu E^*}\) to ∞ and the s-coordinate is integrated only over the small region \(ds\). If the transmission coefficient is factored out of the integral (treating it as a multiplicative factor), the integral over \(p_s\) can be evaluated and yields the following:
\[\kappa \dfrac{kT}{h} \exp(\dfrac{-E^*}{kT}).\]
The exponential energy dependence is usually then combined with the partition function of the TS species that reflect this species’ other \(3N-7\) vibrational coordinates and momenta and the reaction rate is then expressed as
\[\text{Rate} = \kappa \dfrac{kT}{h} [AB*] = \kappa \dfrac{kT}{h} \dfrac{q_{AB}^* /V}{(q_A/V)( q_B/V)} [A] [B].\]
This implies that the rate coefficient \(k_{\rm rate}\) for this bimolecular reaction is given in terms of molecular partition functions by:
\[k_{\rm rate} = k \dfrac{k_T}{h} \dfrac{q_{AB}^*/V}{(q_A/V)(q_B/V)},\]
which is the fundamental result of TST. Once again we notice that ratios of partition functions per unit volume can be used to express ratios of species concentrations (in number of molecules per unit volume), just as appeared in earlier expressions for equilibrium constants as in Chapter 7.
The above rate expression undergoes only minor modifications when unimolecular reactions are considered. For example, in the hypothetical reaction \(A \rightarrow B\) via the TS (\(A^*\)), one obtains
\[k_{\rm rate} = \kappa \dfrac{kT}{h} \dfrac{q_A^*/V}{q_A/V},\]
where again \(q_A^*\) is a partition function of A* with one missing vibrational component.
Before bringing this discussion of TST to a close, I need to stress that this theory is not exact. It assumes that the reacting molecules are nearly in thermal equilibrium, so it is less likely to work for reactions in which the reactant species are prepared in highly non-equilibrium conditions. Moreover, it ignores tunneling by requiring all reactions to proceed through the TS geometry. For reactions in which a light atom (i.e., an H or D atom) is transferred, tunneling can be significant, so this conventional form of TST can provide substantial errors in such cases (however, there are straightforward approximations similar to those we discussed in Chapter 2 that can be used to make tunneling corrections to this rate expression). Nevertheless, TST remains the most widely used and successful theory of chemical reaction rates and can be extended to include tunneling and other corrections as we now illustrate.
Variational Transition State Theory
Within the TST expression for the rate constant of a bi-molecular reaction, \(k_{\rm rate} = \kappa\dfrac{kT}{h} \dfrac{q_{AB}^*/V}{(q_A/V)(q_B/V)}\) or of a uni-molecular reaction, \(k_{\rm rate} = \kappa\dfrac{kT}{h} \dfrac{q_A^*/V}{q_A/V}\), the height (E^*) of the barrier on the potential energy surface appears in the TS species’ partition function \(q_{AB}^*\) or \(q_A^*\), respectively. In particular, the TS partition function contains a factor of the form \(\exp(-E^*/kT)\) in which the Born-Oppenheimer electronic energy of the TS relative to that of the reactant species appears. This energy \(E^*\) is the value of the potential energy \(E(S)\) at the TS geometry, which we denote \(S_0\).
It turns out that the conventional TS approximation to \(k_{\rm rate}\) over-estimates reaction rates because it assumes all trajectories that cross the TS proceed onward to products unless the transmission coefficient is included to correct for this. In the variational transition state theory (VTST), one does not evaluate the ratio of partition functions appearing in \(k_{\rm rate}\) at \(S_0\), but one first determines at what geometry (S*) the TS partition function (i.e., \(q_{AB}^*\) or \(q_A^*\)) is smallest. Because this partition function is a product of (i) the \(\exp(-E(S)/kT)\) factor as well as (ii) 3 translational, 3 rotational, and \(3N-7\) vibrational partition functions (which depend on \(S\)), the value of \(S\) for which this product is smallest need not be the conventional TS value \(S_0\). What this means is that the location (S*) along the reaction path at which the free-energy reaches a saddle point is not the same the location \(S_0\) where the Born-Oppenheimer electronic energy \(E(S)\) has its saddle. This interpretation of how \(S^*\) and \(S_0\) differ can be appreciated by recalling that partition functions are related to the Helmholtz free energy \(A\) by \(q = \exp(-A/kT)\); so determining the value of \(S\) where \(q\) reaches a minimum is equivalent to finding that \(S\) where the free energy \(A\) is at a maximum.
So, in VTST, one adjusts the dividing surface (through the location of the reaction coordinate S) to first find that value \(S^*\) where \(k_{\rm rate}\) has a minimum. One then evaluates both \(E(S^*)\) and the other components of the TS species’ partition functions at this value \(S^*\). Finally, one then uses the \(k_{\rm rate}\) expressions given above, but with \(S\) taken at \(S^*\). This is how VTST computes reaction rates in a somewhat different manner than does the conventional TST. As with TST, the VTST, in the form outlined above, does not treat tunneling and the fact that not all trajectories crossing \(S^*\) proceed to products. These corrections still must be incorporated as an add-on to this theory (i.e., in the k factor for recrossing and through tunneling corrections) to achieve high accuracy for reactions involving light species (recall from Chapter 2 that tunneling probabilities depend exponentially on the mass of the tunneling particle). I refer the reader to the web page of Prof. Don Truhlar, who has been one of the pioneers of VTST for further details.
Reaction Path Hamiltonian Theory
Let us review what the reaction path is as defined earlier in Chapter 3. It is a path that
- begins at a transition state (TS) and evolves along the direction of negative curvature on the potential energy surface (as found by identifying the eigenvector of the Hessian matrix \(H_{j,k} = \dfrac{∂^2E}{∂q_k∂q_j}\) that belongs to the negative eigenvalue);
- moves further downhill along the gradient vector \(\textbf{g}\) whose components are \(g_k = \dfrac{∂E}{∂q_k}\),
- terminates at the geometry of either the reactants or products (depending on whether one began moving away from the TS forward or backward along the direction of negative curvature).
The individual steps along the reaction coordinate can be labeled \(S_0\), \(S_1\), \(S_2\), … \(S_P\) as they evolve from the TS to the products (labeled S_P) and \(S-R\), \(S-R+1\), …\(S_0\) as they evolve from reactants (S-R) to the TS. If these steps are taken in very small (infinitesimal) lengths, they form a continuous path and a continuous coordinate that we label \(S\).
At any point \(S\) along a reaction path, the Born-Oppenheimer potential energy surfacef \(E(S)\), its gradient components
\[g_k(S) = \dfrac{∂E(S)}{∂q_k}\]
and its Hessian components
\[H_{k,j}(S) = \dfrac{∂^2E(S)}{∂q_k∂q_j}\]
can be evaluated in terms of derivatives of \(E\) with respect to the \(3N\) Cartesian coordinates of the molecule. However, when one carries out reaction path dynamics, one uses a different set of coordinates for reasons that are similar to those that arise in the treatment of normal modes of vibration as given in Chapter 3. In particular, one introduces \(3N\) mass-weighted coordinates \(x_j = q_j \sqrt{m_j}\) that are related to the \(3N\) Cartesian coordinates \(q_j\) in the same way as we saw in Chapter 3.
The gradient and Hessian matrices along these new coordinates {x_j} can be evaluated in terms of the original Cartesian counterparts:
\[g_{K’}(S) = \dfrac{g_k(S)}{\sqrt{m_k}}\]
\[ H_{j,k}’ = \dfrac{H_{j,k}}{\sqrt{m_jm_k}}.\]
The eigenvalues {\(\omega_k^2\)} and eigenvectors {\(\textbf{v}_k\)} of the mass-weighted Hessian \(H’\) can then be determined. Upon doing so, one finds
- 6 zero eigenvalues whose eigenvectors describe overall rotation and translation of the molecule;
- \(3N-7\) positive eigenvalues {\(\omega_K^2\)} and eigenvectors \(\textbf{v}_K\) along which the gradient \(\textbf{g}\) has zero (or nearly so) components;
- and one eigenvalue \(\omega_S^2\) (that may be positive, zero, or negative) along whose eigenvector \(\textbf{v}_S\) the gradient \(\textbf{g}\) has its largest component.
The one unique direction along \(\textbf{v}_S\) gives the direction of evolution of the reaction path (in these mass-weighted coordinates). All other directions (i.e., within the space spanned by the \(3N-7\) other vectors \(\{\textbf{v}_K\}\)) possess (nearly) zero gradient component and positive curvature. This means that at any point \(S\) on the reaction path being discussed
- one is at or near a local minimum along all \(3N-7\) directions \(\{\textbf{v}_K\}\) that are transverse to the reaction path direction (i.e., the gradient direction);
- one can move to a neighboring point on the reaction path by moving a small (infinitesimal) amount along the gradient.
- In terms of the \(3N-6\) mass-weighted Hessian’s eigen-mode directions ({\(\textbf{v}_K\)} and \(\textbf{v}_S\)), the potential energy surface can be approximated, in the neighborhood of each such point on the reaction path \(S\), by expanding it in powers of displacements away from this point. If these displacements are expressed as components \(\delta X_k\) along the \(3N-7\) eigenvectors \(\textbf{v}_K\) and \(\delta S\) along the gradient direction \(\textbf{v}_S\),
one can write the Born-Oppenheimer potential energy surface locally as:
\[E = E(S) + \textbf{g}\cdot \textbf{v}_S \delta S + \dfrac{1}{2} \omega_S^2 \delta S^2 + \sum_{K = 1}^{3N-7} \dfrac{1}{2} \omega_K^2 \delta X_K^2 .\]
Within this local quadratic approximation, \(E\) describes a sum of harmonic potentials along each of the \(3N-7\) modes transverse to the reaction path direction. Along the reaction path, \(E\) appears with a non-zero gradient \(\textbf{g}·\textbf{v}_S\) and a curvature \(\dfrac{1}{2} \omega_S^2\) that may be positive, negative, or zero.
The eigenmodes of the local (i.e., in the neighborhood of any point \(S\) along the reaction path) mass-weighted Hessian decompose the \(3N-6\) internal coordinates into \(3N-7\) along which \(E\) is harmonic and one (\(S\)) along which the reaction evolves. In terms of these same coordinates, the kinetic energy \(T\) can also be written and thus the classical Hamiltonian \(H = T+V\) can be constructed. Because the coordinates we use are mass-weighted, in Cartesian form the kinetic energy \(T\) contains no explicit mass factors:
\[T = \dfrac{1}{2} \sum_j m_j \left(\frac{dq_j}{dt}\right)^2 = \dfrac{1}{2} \sum_j \left(\frac{dx_j}{dt}\right)^2.\]
This means that the momenta conjugate to each (mass-weighted) coordinate \(x_j\), obtained in the usual way as
\[p_j = ∂[T-V]/∂(\frac{dx_j}{dt}) = \frac{dx_j}{dt},\]
all have identical (unit) mass factors associated with them.
To obtain the working expression for the reaction path Hamiltonian (RPH), one must transform the above equation for the kinetic energy \(T\) by replacing the \(3N\) Cartesian mass-weighted coordinates {\(x_j\)} by
- the \(3N-7\) eigenmode displacement coordinates \(\delta X_j\),
- the reaction path displacement coordinate \(\delta S\), and
- 3 translation and 3 rotational coordinates.
The three translational coordinates can be separated and ignored (because center-of-mass energy is conserved) in further consideration. The 3 rotational coordinates do not enter into the potential \(E\), but they do appear in \(T\). However, it is most common to ignore their effects on the dynamics that occurs in the internal-coordinates; this amounts to ignoring the effects of overall centrifugal forces on the reaction dynamics. We will proceed with this approximation in mind although the reader should keep in mind that doing so is an approximation that one might have to revisit in more sophisticated treatments.
Although it is tedious to perform the coordinate transformation of \(T\) outlined above, it has been done in the paper W. H. Miller, N. C. Handy and J. E. Adams, Reaction Path Hamiltonian for Polyatomic Molecules, J. Chem. Phys. 72, 99-112 (1980), and results in the following form for the RPH:
\[H = \sum_{K=1}^{3N-7} \dfrac{1}{2}[p_K^2 + \delta X_K^2 \omega_K^2(S)] + E(S) + \dfrac{1}{2} \dfrac{[p_S - \sum_{K,K’=1}^{3N-7} p_K \delta X_{K’} B_{K,K’}]^2}{1+F}\]
where
\[(1+F) = [1 + \sum_{K=1}^{3N-7} \delta X_K B_{K,S}]^2.\]
In the absence of the so-called dynamical coupling factors \(B_{K,K’}\) and \(B_{K,S}\), this expression for \(H\) describes
- \(3N-7\) harmonic-oscillator Hamiltonian \(\dfrac{1}{2}[p_K^2 + \delta X_K^2\omega_K^2(S)]\) each of which has a locally defined frequency \(\omega_K(S)\) that varies along the reaction path (i.e., is \(S\)-dependent);
- a Hamiltonian \(\dfrac{1}{2} p_S^2 + E(S)\) for motion along the reaction coordinate \(S\) with \(E(S)\) serving as the potential.
In this limit (i.e., with the \(B\) factors turned off), the reaction dynamics can be simulated in what is termed a vibrationally adiabatic manner by
- placing each transverse oscillator into a quantum level \(\textbf{v}_K\) that characterizes the reactant’s population of this mode;
- assigning an initial momentum \(p_S(0)\) to the reaction coordinate that is characteristic of the collision to be simulated (e.g., \(p_S(0)\) could be sampled from a Maxwell-Boltzmann distribution if a thermal reaction is of interest, or \(p_S(0)\) could be chosen equal to the mean collision energy of a beam-collision experiment);
- time-evolving the \(S\) and \(p_S\), coordinate and momentum using the above Hamiltonian, assuming that each transverse mode remains in the quantum state \(\textbf{v}_K\) that it had when the reaction began.
The assumption that \(\textbf{v}_K\) remains fixed, which is why this model is called vibrationally adiabatic, does not mean that the energy content of the \(K^{\rm th}\) mode remains fixed because the frequencies \(\omega_K(S)\) vary as one moves along the reaction path. As a result, the kinetic energy along the reaction coordinate \(\dfrac{1}{2} p_S^2\) will change both because \(E(S)\) varies along \(S\) and because \(\sum_{K=1}^{3N-7} \hbar\omega_K^2(S) [\textbf{v}_K + \dfrac{1}{2}]\) varies along S.
Let’s return now to the RPH theory in which the dynamical couplings among motion along the reaction path and the modes transverse to it are included. In the full RPH, the terms \(B_{K,K’}(S)\) couple modes \(K\) and \(K’\), while \(B_{K,S}(S)\) couples the reaction path to mode \(K\). These couplings express how energy can flow among these various degrees of freedom. Explicit forms for the \(B_{K,K’}\) and \(B_{K,S}\) factors are given in terms of the eigenvectors {\(\textbf{v}_K, \textbf{v}_S\)} of the mass-weighted Hessian matrix as follows:
\[B_{K,K’} = \langle d\textbf{v}_K/dS| \textbf{v}_{K’}\rangle; B_{K,S} = \langle d\textbf{v}_K/dS | \textbf{v}_S\rangle\]
where the derivatives of the eigenvectors {\(d\textbf{v}_K/dS\)} are usually computed by taking the eigenvectors at two neighboring points \(S\) and \(S’\) along the reaction path:
\[\frac{d\textbf{v}_K}{dS} = \frac{\textbf{v}_K(S’) – \textbf{v}_K(S)}{S’-S}.\]
In summary, once a reaction path has been mapped out, one can compute, along this path, the mass-weighted Hessian matrix and the potential \(E(S)\). Given these quantities, all terms in the RPH
\[H = \sum_{K=1}^{3N-7} \dfrac{1}{2}[p_K^2 +\delta X_K^2 \omega_K^2(S)] + E(S) + \dfrac{1}{2} \frac{p_S - \sum_{K,K’=1}^{3N-7} p_K \delta X_{K’} B_{K,K’}]^2}{1+F}\]
are in hand. This knowledge can, subsequently, be used to perform the propagation of a set of classical coordinates and momenta forward in time. For any initial (i.e., \(t = 0\)) momenta \(p_S\) and \(p_K\), one can use the above form for H to propagate the coordinates {\(\delta X_K, \delta S\)} and momenta {\(p_K, p_S\)} forward in time. In this manner, one can use the RPH theory to follow the time evolution of a chemical reaction that begins (\(t = 0\)) with coordinates and moment characteristic of reactants under specified laboratory conditions and moves through a TS and onward to products. Once time has evolved long enough for product geometries to be realized, one can interrogate the values of \(\dfrac{1}{2}[p_K^2 + \delta X_K^2 \omega_K^2(S)]\) to determine how much energy has been deposited into various product-molecule vibrations and of \(\dfrac{1}{2} p_S^2\) to see what the final kinetic energy of the product fragments is. Of course, one also monitors what fraction of the trajectories, whose initial conditions are chosen to represent some experimental situation, progress to product geometries vs. returning to reactant geometries. In this way, one can determine the overall reaction probability.
Classical Dynamics Simulation of Rates
One can also perform classical dynamics simulations of reactive events without using the reaction path Hamiltonian. Following a procedure like that outlined in Chapter 7 where classical condensed-media MD simulations were discussed, one can time-evolve the Newton equations of motion of the molecular reaction species using, for example, the Cartesian coordinates of each atom in the system and with either a Born-Oppenheimer surface or a parameterized functional form (e.g., a force field). Of course, it is essential that whatever function one uses must be able to accurately describe the reactive surface, especially near the transition state (recall, that may force fields do not do so because they do not account for bond breaking and forming).
With each such coordinate having an initial velocity \((dq/dt)_0\) and an initial value \(q_0\), one then uses Newton’s equations written for a time step of duration \(\delta t\) to propagate \(q\) and \(dq/dt\) forward in time according, for example , to the following first-order propagation formula:
\[q(t+\delta t) = q_0 + (dq/dt)_0\delta t\]
\[dq/dt (t+\delta t) = (dq/dt)_0-\delta t[(∂E/∂q)_0/m_q]\]
or using the Verlet algorithm described in Chapter 7. Here m_q is the mass factor connecting the velocity dq/dt and the momentum p_q conjugate to the coordinate q:
\[p_q = m_q dq/dt,\]
and \(-(∂E/∂q)_0\) is the force along the coordinate \(q\) at the initial geometry \(q_0\).
By applying the time-propagation process, one generates a set of new coordinates \(q(t+\delta t)\) and new velocities \(dq/dt(t+\delta t)\) appropriate to the system at time \(t+\delta t\). Using these new coordinates and momenta as \(q_0\) and \((dq/dt)_0\) and evaluating the forces \(-(∂E/∂q)_0\) at these new coordinates, one can again use the Newton equations to generate another finite-time-step set of new coordinates and velocities. Through the sequential application of this process, one generates a sequence of coordinates and velocities that simulate the system’s dynamical behavior.
In using this kind of classical trajectory approach to study chemical reactions, it is important to choose the initial coordinates and momenta in a way that is representative of the experimental conditions that one is attempting to simulate. The tools of statistical mechanics discussed in Chapter 7 guide us in making these choices and allow us efficient methods (e.g., the Monte Carlo technique) for sampling such initial values. When one attempts, for example, to simulate the reactive collisions of an A atom with a BC molecule to produce AB + C, it is not appropriate to consider a single classical (or quantal) collision between A and BC. Why? Because in any laboratory setting,
- The A atoms are probably moving toward the BC molecules with a distribution of relative speeds. That is, within the sample of molecules (which likely contains 1010 or more molecules), some A + BC pairs have low relative kinetic energies when they collide, and others have higher relative kinetic energies. There is a probability distribution \(P(E_{KE})\) for this relative kinetic energy that must be properly sampled in choosing the initial conditions.
- The BC molecules may not all be in the same rotational (\(J\)) or vibrational (\(v\)) state. There is a probability distribution function \(P(J,v)\) describing the fraction of BC molecules that are in a particular \(J\) state and a particular \(v\) state. An ensemble of initial values of the BC molecule's internal vibrational coordinate and momentum as well as its orientation and rotational angular momentum must be selected to represent this \(P(J,v)\).
- When the A and BC molecules collide with a relative motion velocity vector \(v\), they do not all hit head on. Some collisions have small impact parameter \(b\) (the closest distance from A to the center of mass of BC if the collision were to occur with no attractive or repulsive forces), and some have large \(b\)-values (see Figure 8.2). The probability function for these impact parameters is \(P(b) = 2\pi bdb\), which is simply a statement of the geometrical fact that larger \(b\)-values have more geometrical volume element than smaller \(b\)-values.
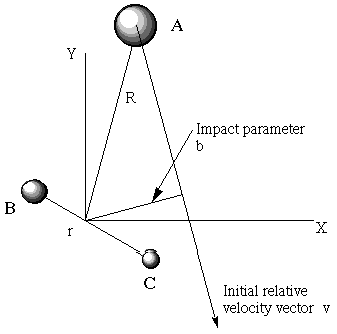
So, to simulate the entire ensemble of collisions that occur between A atoms and BC molecules in various \(J\), \(v\) states and having various relative kinetic energies \(E_{KE}\) and impact parameters b, one must:
- run classical trajectories (or quantum propagations) for a large number of \(J\), \(v\), \(E_{KE}\), and \(b\) values,
- with each such trajectory assigned an overall weighting (or importance factor) of
\[P_{\rm total} = P(E_{KE})P(J,v) 2\pi bdb.\]
After such an ensemble of trajectories representative of an experimental condition has been carried out, one has available a great deal of data. This data includes knowledge of what fraction of the trajectories produced final geometries characteristic of products, so the net reaction probability can be calculated. In addition, the kinetic and potential energy content of the internal (vibrational and rotational) modes of the product molecules can be interrogated and used to compute histograms giving probabilities for observing products in these states. This is how classical dynamics simulations allow us to study chemical reactions and/or energy transfer.
RRKM Theory
Another theory that is particularly suited for studying unimolecular decomposition reactions is named after the four scientists who developed it- Rice, Ramsperger, Kassel, and Marcus. To use this theory, one imagines an ensemble of molecules that have been activated to a state in which they possess a specified total amount of internal energy \(E\) of which an amount \(E^*_{\rm rot}\) exists as rotational energy and the remainder as internal vibrational energy.
The mechanism by which the molecules become activated could involve collisions or photochemistry. It does not matter as long as enough time has passed to permit one to reasonably assume that these molecules have the energy \(E-E^*_{\rm rot}\) distributed randomly among all their internal vibrational degrees of freedom. When considering thermally activated unimolecular decomposition of a molecule, the implications of such assumptions are reasonably clear. For photochemically activated unimolecular decomposition processes, one usually also assumes that the molecule has undergone radiationless relaxation and returned to its ground electronic state but in a quite vibrationally hot situation. That is, in this case, the molecule contains excess vibrational energy equal to the energy of the optical photon used to excite it. Finally, when applied to bimolecular reactions, one assumes that collision between the two fragments results in a long-lived complex. The lifetime of this intermediate must be long enough to allow the energy \(E-E^*_{\rm rot}\), which is related to the fragments’ collision energy, to be randomly distributed among all vibrational modes of the collision complex.
For bimolecular reactions that proceed directly (i.e., without forming a long-lived intermediate), one does not employ RRKM-type theories because their primary assumption of energy randomization almost certainly would not be valid in such cases.
The RRKM expression of the unimolecular rate constant for activated molecules A* (i.e., either a long-lived complex formed in a bimolecular collision or a hot molecule) dissociating to products through a transition state, \(A* \rightarrow TS \rightarrow P\), is
\[k_{\rm rate} = \dfrac{G(E-E_0 –E’_{\rm rot})}{N(E-E^*_{\rm rot})h}.\]
Here, the total energy \(E\) is related to the energies of the activated molecules by
\[E = E^*_{\rm rot} + E^*_{\rm vib}\]
where \(E^*_{\rm rot}\) is the rotational energy of the activated molecule and \(E^*_{\rm vib}\) is the vibrational energy of this molecule. This same energy \(E\) must, of course, appear in the transition state where it is decomposed as an amount \(E_0\) needed to move from A* to the TS (i.e., the energy needed to reach the barrier) and vibrational (\(E'_{\rm vib})\), translational (\(E'_{\rm trans}\) along the reaction coordinate), and rotational (\(E'_{\rm rot}\)) energies:
\[E = E_0 + E’_{\rm vib} + E’_{\rm trans} + E’_{\rm rot} .\]
In the rate coefficient expression, \(G(E-E_0 –E’_{\rm rot} )\) is the total sum of internal vibrational quantum states that the transition state possesses having energies up to and including \(E-E_0 –E’_{\rm rot}\). This energy is the total energy \(E\) but with the activation energy \(E_0\) removed and the overall rotational energy \(E’_{\rm rot}\) of the TS removed. The quantity
\(N(E-E^*_{\rm rot})\) is the density of internal vibrational quantum states (excluding the mode describing the reaction coordinate) that the activated molecule possesses having an energy between \(E-E^*_{\rm rot}\) and \(E-E^*_{\rm rot} + \delta E\). In this expression, the energy \(E-E^*_{\rm rot}\) is the total energy \(E\) with the rotational energy \(E^*_{\rm rot}\) of the activated species removed.
In the most commonly employed version of RRKM theory, the rotational energies of the activated molecules \(E^*_{\rm rot}\) and of the TS \(E’_{\rm rot}\) are assumed to be related by
\[E^*_{\rm rot} – E’_{\rm rot} = J(J+1) \dfrac{h^2}{8\pi^2} \left(\frac{1}{I^*} - \frac{1}{I’}\right) = E^*_{\rm rot} \left(1 –\frac{I^*}{I’}\right).\]
Here \(I^*\) and \(I’\) are the average (taken over the three eigenvalues of the moment inertia tensors) moments of inertia of the activated molecules and TS species, respectively. The primary assumption embodied in the above relationship is that the rotational angular momenta of the activated and TS species are the same, so their rotational energies can be related, as expressed in the equation, to changes in geometries as reflected in their moments of inertia. Because RRKM theory assumes that the vibrational energy is randomly distributed, its fundamental rate coefficient equation
\[k_{\rm rate} = \dfrac{G(E-E_0 –E’_{\rm rot} )}{N(E-E^*_{\rm rot})h} \]
depends on the total energy \(E\), the energy \(E_0\) required to access the TS, and the amount of energy contained in the rotational degrees of freedom that is thus not available to the vibrations.
To implement a RRKM rate coefficient calculation, one must know
- the total energy \(E\) available,
- the barrier energy \(E_0\),
- the geometries (and hence the moments of inertia \(I^*\) and \(I’\)) of the activated molecules and of the TS, respectively,
- the rotational energy \(E^*_{\rm rot}\) of the activated molecules, as well as
- all \(3N-6\) vibrational energies of the activated molecules and all \(3N-7\) vibrational energies of the TS (i.e., excluding the reaction coordinate).
The rotational energy of the TS species can then be related to that of the activated molecules through
\[E^*_{\rm rot} – E’_{\rm rot} = E^*_{\rm rot} \left(1 –\frac{I^*}{I’}\right).\]
To simulate an experiment in which the activated molecules have a thermal distribution of rotational energies, the RRKM rate constant is computed for a range of \(E^*_{\rm rot}\) values and then averaged over \(E^*_{\rm rot}\) using the thermal Boltzmann population
\[(2J+1) \exp\Big(-J(J+1) \dfrac{h^2}{8\pi^2I^*kT}\Big) \]
as a weighting factor. This can be carried out, for example, using the MC process for selecting rotational \(J\) values. This then produces a rate constant for any specified total energy E. Alternatively, to simulate experiments in which the activated species are formed in bimolecular collisions at a specified energy \(E\), the RRKM rate coefficient is computed for a range of \(E^*_{\rm rot}\) values with each \(E^*_{\rm rot}\) related to the collisional impact parameter \(b\) that we discussed earlier. In that case, the collisional angular momentum \(J\) is given as \(J = \mu vb\), where \(v\) is the relative collision speed (related to the collision energy) and m is the reduced mass of the two colliding fragments. Again using \(E^*_{\rm rot} – E’_{\rm rot} = E^*_{\rm rot} \left(1 –\frac{I^*}{I’}\right)\) the TS rotational energy can be related to that of the activated species. Finally, the RRKM rate coefficient is evaluated by averaging the result over a series of impact parameters \(b\) (each of which implies a \(J\) value and thus an \(E^*_{\rm rot}\)) with \(2\pi bdb\) as the weighting factor.
he evaluation of the sum of states \(G(E-E_0 –E’_{\rm rot} )\) and the density of states \(N(E-E^*_{\rm rot})\) that appear in the RRKM expression is usually carried out using a state-counting algorithm such as that implemented by Beyer and Swinehart in Commun. Assoc. Comput. Machin. 16, 372 (1973). This algorithm uses knowledge of the \(3N-6\) harmonic vibrational frequencies of the activated molecules and the \(3N-7\) frequencies of the TS and determines how many ways a given amount of energy can be distributed among these modes. By summing over all such distributions for energy varying from zero to \(E\), the algorithm determines G(E). By taking the difference \(G(E+\delta E) – G(E)\), it determines \(N(E)\delta E\). Professor Bill Hase has been one of the early pioneers involved in applying RRKM theory to chemical processes.
Correlation Function Expressions for Rates
Recall from Chapter 6 that rates of photon absorption can, in certain circumstances, be expressed either in terms of squares of transition dipole matrix elements connecting each initial state \(\Phi_i\) to each final state \(\Phi_f\),
\[| \textbf{E}_0 \cdot \langle \Phi_f | \boldsymbol{\mu} | \Phi_i \rangle |^2\]
or in terms of the equilibrium average of the product of a transition dipole vector at time \(t=0\) dotted into this same vector at another time \(t\)
\[\sum_i \rho_i \langle \Phi_i | \textbf{E}_0 \cdot \boldsymbol{\mu} \textbf{E}_0 · \boldsymbol{\mu} (t) | \Phi_i \rangle\]
That is, these rates can be expressed either in a state-to-state manner or in a time-dependent correlation function framework. In Chapter 7, this same correlation function approach was examined further.
In an analogous fashion, it is possible to express chemical reaction rate constants in a time-domain language again using time correlation functions. The TST (or VTST) and RRKM expressions for the rate constant \(k_{rate}\) all involve, through the partition functions or state densities, the reactant and transition-state energy levels and degeneracies. These theories are therefore analogs of the state-to-state photon-absorption rate equations.
To make the connection between the state-to-state and time-correlation function expressions, one can begin with a classical expression for the rate constant given below:
\[k(t)=\frac{1}{Q_r(2\pi \hbar)^L}\int dpdq e^{-\beta H(q,p)} F(p,q) \chi(p,q)\]
Here
- \(Q_r\) is the partition function of the reactant species,
- L is the number of coordinates and momenta upon which the Hamiltonian \(H(\textbf{p},\textbf{q})\) depends, and
- \(\beta\) is \(1/kT\).
The flux factor \(F\) and the reaction probability \(c\) are defined in terms of a dividing surface which could, for example, be a plane perpendicular to the reaction coordinate \(S\) and located along the reaction path that was discussed earlier in this Chapter in Section 8.1.3. Points on such a surface can be defined by specifying one condition that the L coordinates {qj} must obey, and we write this condition as
\[f(\textbf{q}) = 0.\]
Points lying where \(f(\textbf{q}) < 0\) are classified as lying in the reactant region of coordinate space, while those lying where \(f > 0\) are in the product region. For example, if the dividing surface is defined as being a plane perpendicular to the reaction path, the function f can be written as:
\[f(\textbf{q}) = (S(\textbf{q}) - S_0).\]
Here, \(S\) is the reaction coordinate (which, of course, depends on all of the \(q\) variables) and \(S_0\) is the value of \(S\) at the dividing surface. If the dividing surface is placed at the transition state on the energy surface, \(S_0\) vanishes because the transition state is then, by convention, the origin of the reaction coordinate.
So, now we see how the dividing surface can be defined, but how are the flux \(F\) and probability c constructed? The flux factor \(F\) is defined in terms of the dividing surface function \(f(\textbf{q})\) as follows:
\[F(\textbf{p},\textbf{q}) = \frac{d h(f(\textbf{q}))}{dt}\]
\[= \dfrac{dh}{df} \dfrac{df}{dt}\]
\[=\dfrac{dh}{df} \sum_j \dfrac{∂f}{∂q_j} \dfrac{dq_j}{dt}\]
\[= \delta(f(\textbf{q})) \sum_j \dfrac{∂f}{∂q_j} \dfrac{dq_j}{dt}.\]
Here, \(h(f(\textbf{q}))\) is the Heaviside step function (\(h(x) = 1\) if \(x>0; h(x) = 0\) if \(x < 0\)), whose derivative \(dh(x)/dx\) is the Dirac delta function \(\delta(x)\), and the other identities follow by using the chain rule. When the dividing surface is defined in terms of the reaction path coordinate \(S\) as introduced earlier (i.e., \(f(\textbf{q}) = (S - S_0)\)), the factor \(\sum_j \dfrac{∂f}{∂q_j} \dfrac{dq_j}{dt}\) contains only one term when the L coordinates {\(q_j\)} are chosen, as in the reaction path theory, to be the reaction coordinate \(S\) and L-1 coordinates \({q’_j} = q’\) perpendicular to the reaction path. For such a choice, one obtains
\[\sum_j \dfrac{∂f}{∂q_j} \dfrac{dq_j}{dt} = \frac{dS}{dt} = \dfrac{P_S}{m_S}\]
where \(P_S\) is the momentum along \(S\) and \(m_S\) is the mass factor associated with \(S\) in the reaction path Hamiltonian. So, in this case, the total flux factor \(F\) reduces to:
\[F(\textbf{p},\textbf{q}) = \delta(S-S_0) \dfrac{P_S}{m_S}.\]
We have seen exactly this construct before in Section 8.1.2 where the TST expression for the rate coefficient was developed.
The reaction probability factor \(c(\textbf{p},\textbf{q})\) is defined in terms of those trajectories that evolve, at long time \(t \rightarrow \infty\), onto the product side of the dividing surface; such trajectories obey
\[c(\textbf{p},\textbf{q}) = \lim_{t \rightarrow \infty} h(f(q(t))) = 1.\]
This long-time limit can, in turn, be expressed in a form where the flux factor again occurs\[\lim_{t \rightarrow \infty} h(f(q(t)))=\int_0^\infty \frac{dh(f(q(t)))}{dt}dt=\int_0^\infty Fdt\]
In this expression, the flux \(F(t)\) pertains to coordinates \(q(t)\) and momenta \(p(t)\) at \(t > 0\). Because of time reversibility, the integral can be extended to range from \(t = - \infty\) until \(t = \infty\).
Using the expressions for c and for \(F\) as developed above in the equation for the rate coefficient given at the beginning of this Section allows the rate coefficient \(k(T)\) to be rewritten as follows:
\[k(T)=\frac{1}{Q_r(2\pi \hbar)^L}\int dpdq e^{-\beta H(q,p)} F(p,q) \chi(p,q)\]
\[=\frac{1}{Q_r(2\pi \hbar)^L}\int_{-\infty}^\infty dt\int dpdq e^{-\beta H(q,p)} F(p,q) F(p(t),q(t))\]
In this form, the rate constant \(k(T)\) appears as an equilibrium average (represented by the integral over the initial values of the variables \(p\) and \(q\) with the \(Q_r^{-1} (2\pi \hbar)^{-L} \exp(-\beta H)\) weighting factor) of the time correlation function of the flux \(F\):
To evaluate the rate constant in this time-domain framework for a specific chemical reaction, one would proceed as follows.
- Run an ensemble of trajectories whose initial coordinates and momenta \({q.p}\) are selected (e.g., using Monte-Carlo methods discussed in Chapter 7) from a distribution with \(\exp(-\beta H)\) as its weighting factor.
- Make sure that the initial coordinates \({q}\) lie on the dividing surface because the flux expression contains the \(\delta(f(\textbf{q})) \) factor;
- Monitor each trajectory to observe when it again crosses the dividing surface (i.e., when \({q(t)}\) again obeys \(f(q(t)) = 0\); at which time the quantity
- \(F(p(t),q(t))\) can be evaluated as \(F(\textbf{p},\textbf{q}) = \delta(f(\textbf{q})) \sum_j \dfrac{∂f}{∂q_j} \dfrac{dq_j}{dt}\), using the coordinates and momenta at time \(t\) to compute these quantities.
Using a planar dividing surface attached to the reaction path at \(S = S_0\) as noted earlier allows \(F(q,p)\) to be calculated in terms of the initial (\(t=0\)) momentum lying along the reaction path direction as , \(F(\textbf{p},\textbf{q}) = \delta(S-S_0) \dfrac{P_S}{m_S}\) and permits \(F(p(t),q(t))\) to be computed when the trajectory again crosses this surface at at time \(t\) as \(F(p(t),q(t)) = \delta(S-S_0) P_S(t)/m_S\). So, all that is really needed if the dividing surface is defined in this manner is to start trajectories with \(S = S_0\); to keep track of the initial momentum along \(S\); to determine at what times \(t\) the trajectory returns to \(S = S_0\); and to form the product \(\dfrac{P_S}{m_S} \dfrac{P_S(t)}{m_S}\) for each such time. It is in this manner that one can compute flux-flux correlation functions and, thus, the rate coefficient.
Notice that trajectories that undergo surface re-crossings contribute negative terms to the flux-flux correlation function computed as discussed above. That is, a trajectory with a positive initial value of \((\dfrac{P_S}{m_S})\) can, at some later time t, cross the dividing surface with a negative value of \(\dfrac{P_S(t)}{m_S}\) (i.e., be directed back toward reactants). This re-crossing will contribute a negative value, via. the product \(\dfrac{P_S}{m_S}\dfrac{P_S(t)}{m_S}\), to the total correlation function, which integrates over all times. Of course, if this same trajectory later undergoes yet another crossing of the dividing surface at t' with positive \(P_S(t')\), it will contribute a positive term to the correlation function via. \(\dfrac{P_S}{m_S}\dfrac{P_S(t')}{m_S}\). Thus, the correlation function approach to computing the rate coefficient can properly account for surface re-crossings, unlike the TST which requires one to account for such effects in the transmission coefficient k.
Wave Packet Propagation
The discussions in Chapters 1 and 7 should have made it clear that it is very difficult to time-propagate wave functions rigorously using quantum mechanics. On the other hand, to propagate a classical trajectory is relatively straightforward. In addition to the semi-classical tools introduced in Chapter 1, there is another powerful tool that allows one to retain much of the computational ease and convenient interpretation of the classical trajectory approach while also incorporating quantum effects that are appropriate under certain circumstances. In this wave packet propagation approach, one begins with a quantum mechanical wave function that is characterized by two parameters specifying the average value of the position and of the momentum along each coordinate. One then propagates not the quantum wave function but the values of these two parameters, which one assumes will evolve according to Newtonian dynamics. Let's see how these steps are taken in more detail and try to understand when such an approach is expected to work or to fail.
First, the form of the so-called wave packet quantum function is written as follows:
\[Y(q,Q, P) = \prod_{J=1}^N \frac{1}{\sqrt{2\pi\langle \delta q_J^2\rangle}} \exp\Big[\frac{iP_J q_J}{\hbar} -\frac{(q_J - Q_J)^2}{4}\langle \delta q_J^2\rangle \Big].\]
Here, we have a total of N coordinates that we denote {\(q_J : J=1,N\)}. It is these coordinates that the quantum wave function depends upon. The total wave function is a product of terms, one for each coordinate. Notice that this wave function has two distinct ways in which the coordinate \(q_J\) appear. First, it has a Gaussian spatial dependence (\(\exp\Big[- \dfrac{(q_J - Q_J)^2}{4}\langle \delta q_J^2\rangle \Big]\)) centered at the values \(Q_J\) and having Gaussian width factors related to \(\langle q_J^2\rangle \). This dependence tends to make the wave function's amplitude largest when \(q_J\) is close to \(Q_J\). Secondly, it has a form \(\exp\Big[\dfrac{iP_J q_J}{\hbar}\Big]\) that looks like the travelling wave that we encountered in Chapter 1 in which the coordinate \(q_J\) moves with momentum \(P_J\). So, these wave packet functions have built into them characteristics that allow them to describe motion (via. the \(P_J\)) of an amplitude that is centered at \(Q_J\) with a width given by the parameter \(\langle q_J^2\rangle \).
In this approach to chemical dynamics, we assume the parameters \(P_J\) and \(Q_J\) will undergo classical time evolution according to the Newton equations:
\[\frac{dQ_J}{dt} = \frac{P_J}{m_J}\]
\[\frac{dP_J}{dt} = - \frac{∂V}{∂Q_J}\]
where \(V\) is the potential energy surface (Born-Oppenheimer or force field) upon which we wish to propagate the wave packet, and \(m_J\) is the mass associated with coordinate \(q_J\). For the form of the wave function given above, the \(Q_J\) and \(P_J\) parameters can be shown to be the expectation values of the coordinates \(q_J\) and momenta \(-i\hbar\dfrac{∂}{∂q_J}\):
\[Q_J = \int Y^* q_J Y dq,\]
\[P_J = \int Y^* (- i \hbar\dfrac{∂}{∂q_J}) Y dq.\]
Moreover, the \(\langle q_J^2\rangle \) parameter appearing in the Gaussian part of the function can be shown to equal the dispersion or spread of this wave function along the coordinate \(q_J\):
\[\langle q_J^2\rangle = \int Y^* (q_J - Q_J)^2 Y dq.\]
There is an important characteristic of the above Gaussian wave packet functions that we need to point out. It turns out that functions of the form:
\[Y(q,Q(t), P(t)) = \prod_{J=1}^N \frac{1}{\sqrt{2\pi\langle \delta q_J^2\rangle}} \exp\Big[\frac{iP_J(t) q_J}{\hbar} -\frac{(q_J - Q_J(t))^2}{4}\langle \delta q_J^2\rangle \Big]\]
can be shown to have uncertainties in \(q_J\) and in \(- i \hbar\dfrac{∂}{∂q_J}\) whose product is as small as possible:
\[\langle (q_J –Q_J)^2\rangle \langle (- i \hbar\dfrac{∂}{∂q_J} – P_J)^2\rangle = \dfrac{\hbar^2}{4}.\]
The proof that the wave packet form of the wave function has the smallest uncertainty product is given in the text book Quantum Mechanics, 3rd ed., L. I. Schiff, McGraw-Hill, New York (1968). The Heisenberg uncertainty relation, which is discussed in many texts dealing with quantum mechanics, says that this product of coordinate and momentum dispersions must be greater than or equal to \(\dfrac{\hbar^2}{4}\). In a sense, the Gaussian wave packet function is the most classical function that one can have because its uncertainty product is as small as possible (i.e., equals \(\dfrac{\hbar^2}{4}\)). We say this is the most classical possible quantum function because in classical mechanics, both the coordinate and the momentum can be known precisely. So, whatever quantum wave function allows these two variables to be least uncertain is the most classical.
To use wave packet propagation to simulate a chemical dynamics event, one begins with a set of initial classical coordinates and momenta {\(Q_J(0), P_J(0)\)} as well as a width \(\langle q_J^2\rangle \) or uncertainty for each coordinate. Each width must be chosen to represent the range of that coordinate in the experiment that is to be simulated. For example, assume one were to represent the dynamics of a wave function that is prepared by photon absorption of a \(v = 0\) vibrational state of the H-Cl molecule from the ground 1S state to an excited-state energy surface (\(V(R)\)). Such a situation is described qualitatively in Figure 8.3. In this case, one could choose \(\langle \delta R^2\rangle\) to be the half width of the \(v = 0\) harmonic (or Morse) oscillator wave function \(\chi_0(R)\) of H-Cl, and take \(P(0) = 0\) (because this is the average value of the momentum for \(\chi_0\)) and \(R(0) = R_{\rm eq}\), the equilibrium bond length.
For such initial conditions, classical Newtonian dynamics would then be used to propagate the \(Q_J\) and \(P_J\). In the H-Cl example, introduced above, this propagation would be performed using the excited-state energy surface for \(E\) since, for \(t \rangle 0\), the molecule is assumed to be on this surface. The total energy at which the initial wave packet it delivered to the upper surface would be dictated by the energy of the photon used to perform the excitation. In Figure 8.3, two such examples are shown.
Once the packet is on the upper surface, its position \(Q\) and momentum \(P\) begin to change according to the Newton equations. This, in turn, causes the packet to move as shown for several equally spaced time steps in Figure 8.3 for the two different photons’ cases. At such subsequent times, the quantum wave function is then assumed, within this model, to be given by:
\[Y(q,Q(t), P(t)) = \prod_{J=1}^N \frac{1}{\sqrt{2\pi\langle \delta q_J^2\rangle}} \exp\Big[\frac{iP_J(t) q_J}{\hbar} -\frac{(q_J - Q_J(t))^2}{4}\langle \delta q_J^2\rangle \Big].\]
That is, it is taken to be of the same form as the initial wave function but to have simply moved its center from \(Q(0)\) to \(Q(t)\) with a momentum that has changed from \(P(0)\) to \(P(t)\).
It should be noticed that the time evolution of the wave packet shown in Figure 8.3 displays clear classical behavior. For example, as time evolves, it moves to large R-values and its speed (as evidenced by the spacings between neighboring packets for equal time steps) is large when the potential is low and small when the potential is higher. As we learned in Chapter 6, the time correlation function
\[C(t) = \langle Y(q,Q(0),P(0))|Y(q,Q(t),P(t))\rangle \]
can be used to extract spectral information by Fourier transformation. For the H-Cl example considered here, this correlation function will be large at \(t = 0\) but will decay in magnitude as the wave packet \(Y(q,Q(t),P(t))\) moves to the right (at t1, t2, etc.) because its overlap with \(Y(q,Q(0),P(0))\) becomes smaller and smaller as time evolves. This decay in \(C(t)\) will occur more rapidly for the high-energy photon case because \(Y(q,Q(t),P(t))\) moves to the right more quickly because the classical momentum \(P(t)\) grows more rapidly. These dynamics will induce exponential decays in \(C(t)\) (i.e., \(C(t)\) will vary as \(\exp(-t/\tau_1)\)) at short times.
In fact, the decay of \(C(t)\) discussed above produces, when \(C(t)\) is Fourier transformed, the primary characteristic of the correlation function for the higher-energy photon case where dissociation ultimately occurs. In such photo-dissociation spectra, one observes a Lorentzian line shape whose width is characterized by the decay rate (\(1/\tau_1\)), which, in turn, relates to the total energy of the packet and the steepness of the excited-state surface. This steepness determines how fast \(P(t)\) grows, which then determines how fast the H-Cl bond fragments.
In the lower-energy photon case shown in Figure 8.3, a qualitatively different behavior occurs in \(C(t)\) and thus in the spectrum. The packet’s movement to larger \(R\) causes \(C(t)\) to initially undergo \(\exp(-t/\tau_1)\) decay. However, as the packet moves to its large-R turning point (shortly after time \(t_3\)), it strikes the outer wall of the surface where it is reflected. Subsequently, it undergoes motion to smaller R, eventually returning to its initial value of R. Such recurrences, which occur on time scales that we denote \(\tau_2\), are characteristic of bound motion in contrast to the directly dissociative motion discussed earlier. This recurrence will cause \(C(t)\) to again achieve a large amplitude, but, \(C(t)\) will subsequently again undergo \(\exp(-t/\tau_1)\) decay as the packet once again departs. Clearly, the correlation function will display a series of recurrences followed by exponential decays. The frequency of the recurrences is determined by the frequency with which the packet traverses from its inner to outer turning points and back again, which is proportional to \(1/\tau_2\). This, of course, is the vibrational period of the H-Cl bond. So, in such bound-motion cases, the spectrum (i.e., the Fourier transform of C(t)) will display a series of peaks spaced by (\(1/\tau_2\)) with the envelope of such peaks having a width determined by \(1/\tau_1\).
In more complicated multi-mode cases (e.g., in molecules containing several coordinates), the periodic motion of the wave packet usually shows another feature that we have not yet discussed. Let us, for simplicity, consider a case in which only two coordinates are involved. For the wave packet to return to (or near) its initial location, enough time must pass for both coordinates to have undergone an excursion to their turning points and back. For example, consider the situation in which one coordinate’s vibrational frequency is ca. 1000 cm-1 and the other’s is 300 cm-1; these two modes then require ca. 1/30 ps and 1/9 ps, respectively, to undergo one complete oscillation. At \(t = 0\), the wave packet, which is a product of two packets, \(\prod_{J=1}^2 \dfrac{1}{\sqrt{2\pi\langle \delta q_J^2\rangle}} \exp\Big[\dfrac{iP_J(t) q_J}{\hbar} -\dfrac{(q_J - Q_J(t))^2}{4}\langle \delta q_J^2\rangle \Big]\), one for each mode, produces a large C(t). After 1/30 ps, the first mode’s coordinate has returned to its initial location, but the second mode is only 9/30 of the way along in its periodic motion. Moreover, after 1/9 ps, the second mode’s coordinate has returned to near where it began, but now the first mode has moved away. So, at both 1/30 ps and 1/9 ps, the correlation function will not be large because one of the mode contribution to \(C(t) = \langle Y(q,Q(0),P(0)) | Y(q,Q(t),P(t))\rangle\) will be small. However, after 1/3 ps, both modes’ coordinates will be in positions to produce a large value of C(t); the high-frequency mode will have undergone 10 oscillations, and the lower-frequency mode will have undergone 3 oscillations. My point in discussing this example is to illustrate that molecules having many coordinates can produce spectra that display rather complicated patterns but which, in principle, can be related to the time evolution of these coordinates using the correlation function’s connection to the spectrum.
Of course, there are problems that arise in using the wave packet function to describe the time evolution of a molecule (or any system that should be treated using quantum mechanics). One of the most important limitations of the wave packet approach to be aware of relates to it inability to properly treat wave reflections. It is well know that when a wave strikes a hard wall, it is reflected by the wall. However, when, for example, a water wave moves suddenly from a region of deep water to a much more shallow region, one observes both a reflected and a transmitted wave. In the discussion of tunneling resonances given in Chapter 2, we also encountered reflected and transmitted waves. Furthermore, when a wave strikes a barrier that has two or more holes or openings in it, one observes wave fronts coming out of these openings. The problem with the most elementary form of wave packets presented above is that each packet contains only one piece. It therefore can not break into two or more pieces as it, for example, reflects from turning points or passes through barriers with holes. Because such wave packets can not fragment into two or more packets that subsequently undergo independent dynamical evolution, they are not able to describe dynamical processes that require multiple-fragmentation events. It is primarily for this reason that wave packet approaches to simulating dynamics are usually restricted to treating short-time dynamics where such fragmentation of the wave packet is less likely to occur. Prompt molecular photo-dissociation processes such as we discussed above is a good example of such a short-time phenomenon. There have been many refinements of the wave packet approach described above, some of which are designed to allow for splitting of the wave function. I refer the reader to the work of one of the pioneers of the time-dependent wave packet approach, Prof. Eric Heller, for more information on this subject.
Surface Hopping Dynamics
There are, of course, chemical reactions and energy-transfer collisions in which two or more Born-Oppenheimer (BO) energy surfaces are involved. Under such circumstances, it is essential to have available the tools needed to describe the coupled electronic and nuclear-motion dynamics appropriate to this situation.
The way this problem is addressed is by returning to the Schrödinger equation before the single-surface BO approximation was made and expressing the electronic wave function \(\Psi(\textbf{r}|\textbf{R})\), which depends on the electronic coordinates {\(\textbf{r}\)} and the nuclear coordinates \(\{R\}\), as:
\[\Psi(\textbf{r}|\textbf{R})=\sum_J a_J(t)\psi_J(\textbf{r}|\textbf{R})\]
Here, \(\psi_J(\textbf{r}|\textbf{R})\) can be the BO electronic wave function belonging to the \(J^{\rm th}\) electronic state, in which case we say we are using an adiabatic basis of electronic states. The \(a_J(t)\) are amplitudes that will relate to the probability that the system is on the \(J^{\rm th}\) energy surface. Next, we assume that the coordinates {\(\textbf{R}(t)\)} of the nuclei undergo classical motion in a manner to be specified in further detail below that allows us to know their locations and velocities (or momenta) at any time \(t\). This assumption implies that the time dependence of the above wave function is carried in the time dependence of the coordinates \(\textbf{R}(t)\) as well as in the \(a_J(t)\) amplitudes
\[\Psi(\textbf{r}|\textbf{R(t)})=\sum_J a_J(t)\psi_J(\textbf{r}|\textbf{R(t)})\]
We next substitute this expansion into the time-dependent Schrödinger equation
\[i \hbar \dfrac{\partial \psi}{\partial t} = H_0 (\textbf{r}|\textbf{R}(t))\psi\]
where \(H_0 (\textbf{r}|\textbf{R}(t))\) is the electronic Hamiltonian, which depends on the nuclear coordinates \(R(t)\) and thus on the time variable. We then multiply the resultant equation on the left by one of the wave functions \(\psi^*K(\textbf{r}|\textbf{R})\) and integrate over the electronic coordinates {\(\textbf{r}\)} to obtain an equation for the \(a_K(t)\) amplitudes:
\[i\hbar\frac{da_K}{dt}=\sum_J \left[V_K{K,J}(R(t))-i\hbar\langle \psi_K|\dfrac{d\psi_J}{dt}\rangle \right]a_J .\]
Here, \(V_{K,J}\) is the electronic Hamiltonian matrix element that couples \(\psi_K\) to \(\psi_J\). This set of coupled differential equations for the amplitudes can be solved numerically by, for example, starting at \(t_i\) with \(a_K = 1\) and \(a_{J\ne K} = 0\) and propagating the amplitudes’ values forward in time.
The next step is to express \(\langle \psi_K|d\psi_J/dt\rangle \), using the chain rule, in terms of derivatives with respect to the nuclear coordinates {\(\textbf{R}\)} and the time rate of change of these coordinates:
\[\langle \psi_K|\dfrac{d\psi_J}{dt}\rangle =\sum_b\langle \psi_K|\dfrac{d\psi_J}{d\textbf{R}_b}\rangle \dfrac{d\textbf{R}_b}{dt}\]
So, now the equations for the \(a_K(t)\) read as follows:
\[i\hbar\frac{da_K}{dt}=\sum_J \left[V_K{K,J}(R(t))-i\hbar\sum_b \langle \psi_K|\dfrac{d\psi_J}{d\textbf{R}_b}\rangle \dfrac{d\textbf{R}_b}{dt} \right]a_J \]
The
\[\langle \psi_K|\dfrac{d\psi_J}{d\textbf{R}_b}\rangle =\textbf{d}_{K,J}(b)\]
are called non-adiabatic coupling matrix elements (for each pair of states \(K\) and \(J\), they are a vector in the space of the nuclear coordinates \(\textbf{R}\)), and it is their magnitudes that play a central role in determining the efficiency of surface hoppings. Below we will make use of the following symmetry property of these quantities, which derive from the orthogonality of the {\(\psi_J\)}
\[\langle \psi_K|\dfrac{d\psi_J}{d\textbf{R}_b}\rangle =\textbf{d}_{K,J}(b)=-\langle \psi_J|\dfrac{d\psi_K}{d\textbf{R}_b}\rangle ^*=-\textbf{d}_{J,K}^*(b)\]
\[\langle \psi_K|\dfrac{d\psi_K}{d\textbf{R}_b}\rangle =0\]
These matrix elements are becoming more commonly available in widely utilized quantum chemistry and dynamics computer packages (although their efficient evaluation remains a challenge that is undergoing significant study). Qualitatively, one can expect a coupling \(\langle \psi_K|d\psi_J/dRa\rangle\) to be large if motion along a coordinate causes an orbital occupied in \(\psi_J\) to be distorted in a manner that would produce significant overlap with an orbital in \(\psi_K\).
If the electronic functions {\(\psi_K\)} appearing in the equations
\[i\hbar\frac{da_K}{dt}=\sum_J \left[V_K{K,J}(R(t))-i\hbar\sum_b \textbf{d}_{K,J}(b)\dfrac{d\textbf{R}_b}{dt} \right]a_J \]
are BO eigenfunctions, the off-diagonal elements \(V_{K,J}\) vanish and the diagonal elements are the BO energy levels. In this case, only the terms involving \(d_{K,J}(b)\) generate transitions between surfaces. On the other hand, if one chooses electronic functions {\(\psi_K\)} that have vanishing \(d_{K,J}(b)\) values, only the \(V_{K,J}\) terms induce transitions among surfaces. The latter case is said to involve using diabatic wave functions, while the former involves adiabatic wave functions. For the remainder of this discussion, I will assume we are making use of adiabatic (i.e., BO) wave functions, but I will carry through the derivation in a manner that will allow either adiabatic or diabatic functions to be used.
Because one is eventually interested in the populations for being in various electronic states, it is common to recast the above equations for the amplitudes \(a_J(t)\) into equations for so-called density matrix elements
\[\gamma_{K,J}(t)=a_K(t)a_J^*(t)\]
The diagonal elements of the \(\textbf{g}\) matrix are the state probabilities while the off-diagonal elements contain information about the phases of the complex quantities {\(a_J\)}. So, in place of the equations for the {\(a_J(t)\)}, one can use the following equations for the {\(g_{K,J}\)}:
\[i\hbar\frac{d\gamma_{K,J}}{dt}=\sum_L\left\{ \gamma_{L,J}\left[V_{K,L}-i\hbar\sum_b \dfrac{d\textbf{R}_b}{dt} \textbf{d}_{K,J}(b) \right] - \gamma_{K,L}\left[V_{L,J}-i\hbar\sum_b \dfrac{d\textbf{R}_b}{dt} \textbf{d}_{L,J}(b) \right]\right\} \]
Setting \(K=J\), it is then possible to derive an equation for the time evolution of the diagonal elements of the density matrix
\[\frac{d\gamma_{K,K}}{dt}=\sum_{L\ne K}X_{K,L}\]
where
\[X_{K,L}=\frac{2}{\hbar}\Im\{\gamma_{L,K}V_{K,L}\}-2\Re\{\gamma_{L,K}\sum_b \dfrac{d\textbf{R}_b}{dt} \textbf{d}_{K,J}(b)\}\]
In addition to calculating amplitudes (the probabilities then being computed as \(|a_J|^2 = \gamma_{J,J}\)), one often needs to identify (using, perhaps the kind of strategy discussed in Chapter 3) the seam at which the surfaces of interest intersect. This helps focus attention on those geometries near which a surface hop is most likely to occur.
To utilize the most basic form of surface hopping theory, one proceeds as follows:
- One begins with initial values of the nuclear coordinates {\(\textbf{R}_b\)} and their velocities {\(\textbf{R}_b/dt\)} that properly characterize the kind of collision or reaction one wishes to simulate. Of course, one has to utilize an ensemble of trajectories with initial conditions chosen to properly describe such an experimental situation. In addition, one specifies which electronic surface (say the \(K^{\rm th}\) surface) the system is initially on.
- For each such set of initial conditions, one propagates a classical trajectory describing the time evolution of the {Ra} and {dRa/dt} on this initial (\(K^{\rm th}\)) surface.
- As one is propagating the classical trajectory, one also propagates the coupled differential equations for the density matrix elements with the nuclei moving on the \(K^{\rm th}\) energy surface
- After each time-propagation step of duration \(\delta t\), one evaluates the quantity shown above (these elements give estimates for the rate of change of the population of the \(K^{\rm th}\) state due to transitions to other states) from which one computes
.
These quantities control the fractional change in the probability of being on the \(K^{\rm th}\) surface \(\gamma_{K,K}\) due to transitions from state \(K\) into state \(J\). They are used as follows. A random number \(0 < x < 1\) is chosen. If \(x < g_{K,J}\) a hop to surface \(J\) is allowed to occur; otherwise, no hop occurs and the system remains to continue its time evolution on surface K.
- 5. If a hop occurs, the coordinates and momenta are allowed to now propagate on the \(J^{\rm th}\) energy surface, where the forces will, of course, be different, but with one change. The component of the velocity vector along the non-adiabatic coupling vector is modified to allow for the fact that the system’s electronic energy has suddenly changed from \(V_K(R)\) to \(V_J(R)\), which must be compensated for by a change in the kinetic energy of the nuclei so that total energy is conserved. If \(V_K(R) > V_J(R)\), this results in an increase in speed; if \(V_K(R) < V_J(R)\) it produces a decrease in speed. In the latter case, if \(V_K(R)\) lies considerably below \(V_J(R)\), it might turn out that there is just not enough total energy to access the surface \(V_J(R)\); in this case, the hop is not allowed to occur.
- 6. Following the above decision about allowing the hop and adjusting the speed along the direction of the vector, the trajectory is then continued with the system now propagating on the \(J^{\rm th}\) or \(K^{\rm th}\) surface, and the differential equations involving continue to be propagated with no changes other than the fact the nuclei may (or may not) be evolving on a different surface. The entire process is repeated until the trajectory reaches termination (e.g., a reaction or quenching is observed, or some specified time limit is reached) at which time one can probe the properties of the products as reflected in the coordinates and velocities of the nuclei.
Carrying out surface hopping trajectories for an ensemble of trajectories with initial conditions representative of an experiment generates an ensemble of final \(\gamma_{J,J}\) values (i.e., at the end of each trajectory) whose averages can be used to estimate the overall probability of ending up in the \(J^{\rm th}\) electronic state. The algorithm discussed above is the so-called fewest-switches method (detailed in J. C. Tully, J. Chem. Phys. 93, 1061 (1990)) pioneered by Prof. John Tully. This surface-hopping algorithm remains one of the most widely used approaches to treating such coupled-state dynamics.
Landau-Zener Surface Jumps
There is a simplified version of the surface hopping procedure just discussed that is often used when one has two electronic surfaces that intersect in a region of space that (i) is energetically accessible in the experiment being simulated and (ii) can be located and characterized (e.g., in terms of its coordinates and energy gradients) in a computationally feasible manner. To illustrate, we again consider the case of Al interacting with \(H_2\), whose potential energy surfaces are reproduced below from Figure 3.1c.
With the Landau-Zener model described in this Section, trajectories are propagated on one energy surface until a point on or very near the seam (denoted \(\textbf{R}_x(r)\) in Figure 8.3 a) is encountered at which time an equation giving the probability of undergoing a jump to the other surface is invoked. It is the purpose of this Section to derive and explain this Landau-Zener equation.
In Chapter 4, we learned that the rates of transitions from one state (labeled \(i\)) to another (labeled \(f\)) can sometimes be expressed in terms of matrix elements of the perturbation connecting the two states as follows
\[{\rm Rate}=\delta(\omega-\omega_{f,i})\dfrac{2\pi |\langle \Psi_f^0|v(r)|\Psi_i^0\rangle |^2}{\hbar^2}.\]
Because the coupling matrix elements \(\langle \Psi_f^0|v(r)|\Psi_i^0\rangle \) have units of energy, and the \(\delta(\omega-\omega_{f,i})\) function has units of inverse frequency, the rate expression clearly has units of \(s^{-1}\). In the rate equation, is the energy of the transition induced by light of energy , and \(v(r)\) is the perturbation due to the electric dipole operator. These photon-induced rates can be viewed as relating to transitions between two surfaces that cross: (i) one surface being that of the initial state plus a photon of energy , and (ii) the second being that of the final state with no photon. In this point of view, the photon lifts the lower-energy state upward in energy until it crosses the upper state and then the dipole operator effects the transition.
Making analogy with the photon-absorption case, we consider expressing the rates of transitions between
- an initial state consisting of an electronic state multiplied by a state describing the initial vibrational (including inter-fragment collisional) and rotational state of the system,
- a final state consisting of the product of another electronic and vibration-rotation state
as follows
\[{\rm Rate}=\delta(\omega_{f,i})\dfrac{2\pi |\langle \Psi_f^0\chi_f(R)|v(r)|\Psi_i^0\chi_i(R)\rangle |^2}{\hbar^2}.\]
That is, we use the same golden rule rate expression but with no photon energy needed to cause the two surfaces to intersect. Next we use the identity
\[\delta(x)=\frac{1}{2\pi}\int_{-\infty}^{\infty}\exp(ixt)dt\]
to write
\[\delta(\omega_{f,i})=\delta((\varepsilon_f-\varepsilon_i)/\hbar)=\frac{1}{2\pi}\int_{-\infty}^{\infty}\exp\Big(\frac{i(\varepsilon_f-\varepsilon_i)t}{\hbar}\Big)dt.\]
which can be substituted into our rate expression to obtain
\[{\rm Rate}=\frac{1}{2\pi}\int_{-\infty}^{\infty}\exp\Big(\frac{i(\varepsilon_f-\varepsilon_i)t}{\hbar}\Big)
\dfrac{2\pi \langle \Psi_f^0\chi_f(R)|v(r)|\Psi_i^0\chi_i(R)\rangle \langle \Psi_f^0\chi_f(R)|v(r)|\Psi_i^0\chi_i(R)\rangle }{\hbar^2}dt.\]
Defining two nuclear-motion Hamiltonian, one for each BO surface,
\[h_{i,f}=T_R+V_{i,f}(R)\]
and assuming that the nuclear-motion wave functions obey
\[h_{i,f}\chi_{i,f}(R)=\varepsilon_{i,f}\chi_{i,f}(R)\]
this expression becomes
\[{\rm Rate}=\frac{1}{2\pi}\int_{-\infty}^{\infty}\dfrac{2\pi \langle \Psi_f^0\chi_f(R)|v(r)|\Psi_i^0\chi_i(R)\rangle \langle \Psi_f^0\chi_f(R)\exp\Big(\dfrac{ih_ft}{\hbar}\Big)|v(r)|\exp\Big(-\dfrac{ih_ft}{\hbar}\Big)\Psi_i^0\chi_i(R)\rangle }{\hbar^2}dt.\]
In the expression
\[\exp\Big(\dfrac{ih_ft}{\hbar}\Big)|v(r)|\exp\Big(-\dfrac{ih_ft}{\hbar}\Big)\]
the \(\langle \psi_i^0(r)|v(r)|\psi_i^0(r)\rangle \) elements of \(v(r)\) for our surface-jumping problem would involve either the \(V_{i,f}\) electronic Hamiltonian couplings (if one uses a diabatic basis) or the non-adiabatic coupling elements (if one used a BO adiabatic basis). In either case, these elements are functions of the nuclear coordinates and thus do not commute with the differential operators appearing in \(T_R\). As a result, the operator combination \(\exp\Big(\dfrac{ih_ft}{\hbar}\Big)|v(r)|\exp\Big(-\dfrac{ih_ft}{\hbar}\Big)\) must be handled carefully (e.g., as one does in the coupled-cluster expansion treated in Chapter 6) by expanding the exponential operators and keeping track of the fact that not all terms commute. The lowest-order term in the expansion of this combination of operators is
\[\exp\Big(\dfrac{ih_ft}{\hbar}\Big)|v(r)|\exp\Big(-\dfrac{ih_ft}{\hbar}\Big)\approx v(r)\exp\Big(\dfrac{it(V_f(\textbf{R})-V_i(\textbf{R}))}{\hbar}\Big)\]
which yields the approximation I now want to pursue.
Using this approximation in our expression for the rate of surface jumping transitions gives
\[{\rm Rate}=\frac{1}{2\pi}\int_{-\infty}^{\infty}\dfrac{2\pi \langle \Psi_f^0\chi_f(R)|v(r)|\Psi_i^0\chi_i(R)\rangle \langle \chi_f(R)\exp(iV_ft/\hbar)\langle \Psi_f^0|v(r)|\Psi_i^0\rangle \exp(-iV_it/\hbar)\chi_i(R)\rangle }{\hbar^2}dt.\]
We now use
\[\delta(V_f(\textbf{R})-V_i(\textbf{R}))=\frac{1}{2\pi}\int_{-\infty}^{\infty}\exp\Big(\frac{i(V_f(\textbf{R})-V_i(\textbf{R}))t}{\hbar}\Big)dt\]
to write the rate as
\[{\rm Rate}=\frac{2\pi}{\hbar} \langle \chi_f(R)\langle \Psi_f^0|v(r)|\Psi_i^0\rangle \chi_i(R)\rangle \langle \chi_f(R)\langle \Psi_f^0|v(r)|\Psi_i^0\rangle \delta(V_f(\textbf{R})-V_i(\textbf{R}))\chi_i(R)\rangle .\]
\[=\frac{2\pi}{\hbar}\langle \chi_f(R)|v_{f,i}|\chi_i(R)\rangle \langle \chi_f(R)|v_{f,i}|\delta(V_f(\textbf{R})-V_i(\textbf{R}))\chi_i(R)\rangle \]
where we define the electronic transition integrals in shorthand as
\[v_{f,i}=\langle \Psi_f^0|v(r)|\Psi_i^0\rangle \]
Because of the energy-conserving d-function , we can actually simplify this expression even further by summing over the complete set of the final-state’s vibration-rotation functions and making use of the completeness relation
\[\sum_f\chi_f(R)\chi_f^*(R)=\delta(R-R')\]
to obtain
\[{\rm Rate}=\frac{2\pi}{\hbar}\langle \chi_i(R)|v_{f,i}^*v_{f,i}|\delta(V_f(\textbf{R})-V_i(\textbf{R}))\chi_i(R)\rangle .\]
This expression can be seen to have units of s-1 since the delta function has units of inverse energy and each electronic coupling integral has units of energy.
In the above rate expression, we see a d-function that limits the integration to only those geometries for which \(V_i = V_f\) ; these are the geometries that lie on the intersection seam. Any geometry \(\textbf{R}\) can be expressed in terms of the geometry \(\textbf{S}\) of the point on the seam closest to \(\textbf{R}\) plus a displacement of magnitude \(\eta\) along the unit vector normal to the seam at point \(\textbf{S}\)
\[\textbf{R}=\textbf{S}+\hat{\textbf{n}}\eta.\]
If we now expand the energy difference \(V_f(\textbf{R}) – V_i(\textbf{R})\) in a Taylor series about the point \(\textbf{S}\) lying on the seam, we obtain
\[V_f(\textbf{R}) – V_i(\textbf{R})=V_f(\textbf{S}) – V_i(\textbf{S})+\nabla[V_f(\textbf{R}) – V_i(\textbf{R})]_S\bullet\hat{n}(\textbf{S})\eta+\text{ higher - order}\]
The gradient \(\nabla[V_f(\textbf{R}) – V_i(\textbf{R})]_S\) of the potential difference has zero components within the subspace of the seam; its only non-vanishing component lies along the normal \(\hat{n}(\textbf{S})\) vector. Now using
\[\delta(ax)=\frac{1}{|a|}\delta(x),\]
the \(\delta(V_f(\textbf{R}) – V_i(\textbf{R}))\) function can be expressed as
\[\delta(V_f(\textbf{R}) – V_i(\textbf{R}))=\delta((V_f(\textbf{S}) – V_i(\textbf{S}))+\eta\nabla(V_f(\textbf{S}) – V_i(\textbf{S}))\bullet\hat{n}(\textbf{S})+\cdots)\]
\[=\delta(0+\eta\nabla(V_f(\textbf{S}) – V_i(\textbf{S}))\bullet\hat{n}(\textbf{S})+\cdots)=\frac{1}{|\nabla(V_f(\textbf{S}) – V_i(\textbf{S}))\bullet\hat{n}(\textbf{S})|}\delta(\eta)\]
with the \(\delta(h)\) factor constraining the integral to lie within the seam.
\[{\rm Rate}=\frac{2\pi}{\hbar}\int\int \chi_i^*(R)v_{i,f}^*v_{i,f}\frac{\delta(\eta)}{|\nabla(V_f-V_i)|_S}\chi_i(R)dSd\eta\]
\[=\frac{2\pi}{\hbar}\int \chi_i^*(S,0)v_{i,f}^*v_{i,f}\frac{1}{|\nabla(V_f-V_i)|_S}\chi_i(S,0)dS\]
This result can be interpreted as follows:
- \(\chi_i^*(S,0)\chi_i(S,0)\) gives the probability density for being at a point \(\textbf{R}=(\textbf{S},0)\) on the seam; this factor has units of (length)-(3N-6) .
- \(\dfrac{2\pi}{\hbar}v_{i,f}^*v_{i,f}\dfrac{1}{|\nabla(V_f-V_i)|_S}\) gives the rate of transitions from one surface to the other at the point \(\textbf{S}\) on the seam; this factor has units of length times s-1.
- The \(d\textbf{S}\) factor has units of (length) 3N-7; so the entire expression has units of s-1 as it should.
In this form, the rate expression can be used by (i) sampling (e.g., using Monte Carlo) over as much of the seam as is energetically accessible, using the initial-state spatial probability density as a weighting factor, and (ii) forming the sampling average of the rate quantity \(\dfrac{2\pi}{\hbar}v_{i,f}^*v_{i,f}\dfrac{1}{|\nabla(V_f-V_i)|_S}\) computed for each accepted geometry.
There is another way to utilize the above rate expression. If we think of a swarm of \(N\) trajectories (i.e., an ensemble representative of the experiment of interest) and ask what is the rate \(r(\textbf{S})\) at which trajectories pass through a narrow region of thickness \(\eta\) at a point \(\textbf{S}\) on the seam, we could write
\[r(\textbf{S})=N|\chi_i(\textbf{S},\eta)|^2\frac{v_n}{\eta}d\textbf{S}d\eta\]
where \(|\chi_i(\textbf{S},\eta)|^2\) gives the probability density for a trajectory being at the point \(\textbf{S}\) on the seam and lying within a distance \(\eta\) along the direction \(\hat{n}(\textbf{S})\) normal to the seam. The quantity \(\dfrac{v_n}{\eta}\) is the component of the velocity along \(\hat{n}(\textbf{S})\) with which the system moves through the seam divided by the thickness \(\eta\). This ratio gives the inverse of the time the system spends within the thin \(\eta\) region or, equivalently, the frequency of passing through the thin strip of the seam at S. The quantity \(d\textbf{S}d\eta\) is the volume element \(d\textbf{R}\) whose units cancel those of \(|\chi_i(\textbf{S},\eta)|^2\).
If we multiply this rate at which trajectories pass through \(\textbf{S}\), \(\eta\) by the probability \(P\) that a surface jump will occur and integrate over the entire seam space \(d\textbf{S}d\eta\), we can express the rate at which the \(N\) trajectories will undergo jumps
\[{\rm Rate}=\int NP|\chi_i(\textbf{S},\eta)|^2\frac{v_n}{\eta}d\textbf{S}d\eta = \int NP|\chi_i(\textbf{S},\eta)|^2v_n d\textbf{S}.\]
If we divide this rate by \(N\), the number of trajectories, to produce the average rate per trajectory, and compare this expression to the rate we derived earlier
\[{\rm Rate}=\frac{2\pi}{\hbar}\int \chi_i^*(S,0)v_{i,f}^*v_{i,f}\frac{1}{|\nabla(V_f-V_i)|_S}\chi_i(S,0)dS\]
we see that they would be equivalent if the probability \(P\) of a surface jump were given by
\[P=\frac{2\pi}{\hbar}v_{i,f}^*v_{i,f}\frac{1}{v_\eta|\nabla(V_f-V_i)|_S}.\]
The above expression for the probability of jumping from \(V_i(\textbf{R})\) to \(V_f(\textbf{R})\) is known as the Landau-Zener (LZ) formula. The way it is used in most applications is as follows:
- An ensemble of classical trajectories with initial coordinates and momenta selected to represent an experimental condition are run on the potential energy surface \(V_i(\textbf{R})\).
- Whenever any trajectory passes very close to an intersection seam between \(V_i(\textbf{R})\) and another surface \(V_f(\textbf{R})\), the seam geometry \(\textbf{S}\) nearest to \(\textbf{R}\) is determined and the gradient \(\nabla(V_f-V_i)\) of the energy difference is evaluated at \(\textbf{S}\). In addition, the component of the velocity along the direction of this gradient is computed.
- The electronic coupling matrix elements between the two states are evaluated at S, and the above formula is used to estimate the probability \(P\) of a surface jump. In most applications of LZ theory, the electronic states {\(\psi_{i,f}^0\) } in the region of a crossing seam are taken to be diabatic states because then the coupling matrix elements can be taken from the splitting between the two adiabatic states that undergo an avoided crossing near \(\textbf{S}\) rather than by evaluating non-adiabatic coupling matrix elements \(\langle \psi_i|\dfrac{d\psi_f}{dR_b}\rangle \) between adiabatic BO states.
In summary, the LZ expression for the probability of a surface jump should be viewed as an approximate version of the algorithm provided by the fewest-switches surface hopping approach discussed earlier. Before closing this Section, it is useful to point out how this formula applies to two distinct cases
1. If, as suggested in Figure 8.3 b, a molecule is prepared (e.g., by photon absorption) in an excited electronic state (the upper blue curve) that undergoes a crossing with a dissociative electronic state (the green curve), one may wish to estimate the rate of the process called predissociation in which the excited molecule jumps to the dissociative surface and falls apart. This rate is often computed by multiplying the frequency \(\nu\) at which the excited molecule passes through the curve crossing by the LZ estimate of the surface jumping probability P:
\[{\rm Rate}=\nu P\]
with \(P\) computed as discussed above and \(\nu\) usually being equal to the vibrational frequency of the bond whose stretching generates the curve crossing.
igure 8.3b Qualitative depiction of predissociation that can occur from an excited (blue) surface onto a dissociative (green) surface.
2. Alternatively, one may be interested in determining the probability that the fragment species (atoms in Figure 8.3 b) collide on the green curve and undergo a transition to the upper blue curve as a result of this collision. For example, prompt fluorescence from this upper blue curve might be the experimental signature one wishes to simulate. In this case, the outcome (i.e., generation of the molecule in the upper blue curve’s electronic state) can occur in either of two ways:
a. The system collides on the green curve and undergoes a surface jump at the crossing, thus ending up on the blue surface from which it promptly fluoresces; this process has a probability \(P\) computed using the LZ formula.
b. The system collides on the green curve and does not jump to the blue curve at the crossing, but remains on the green curve (this has probability \(1-P\)) until it reaches the turning point. After reflecting off the turning point, the system (still on the green curve) jumps to the blue curve (this has probability \(P\)) when it again reaches the crossing after which prompt fluorescence occurs. The overall probability for this path is \(P(1-P)\).
So, the total yield of fluorescence would be related to the quantity \(P + P(1-P)\). The point of these two examples is that the LZ formula gives an estimate of the jump probability for a given crossing event; one still needs to think about how various crossing events relate to the particular experiment at hand.
Contributors and Attributions
Jack Simons (Henry Eyring Scientist and Professor of Chemistry, U. Utah) Telluride Schools on Theoretical Chemistry
Integrated by Tomoyuki Hayashi (UC Davis)


