6.4: Deficiencies in the Single Determinant Model
- Page ID
- 162849
To achieve reasonable chemical accuracy (e.g., ± 5 kcal/mole in EAs or IPs or bond energies) in electronic structure calculations, one can not describe the wavefunction \(\psi\) in terms of a single determinant. The reason such a wavefunction is inadequate is because the spatial probability density functions are not correlated. This means the probability of finding one electron at position r is independent of where the other electrons are, which is absurd because the electrons’ mutual Coulomb repulsion causes them to avoid one another. This mutual avoidance is what we call electron correlation because the electrons’ motions, as reflected in their spatial probability densities, are correlated (i.e., inter-related). Let us consider a simple example to illustrate this problem with single determinant functions. The \(|1s\alpha(r) 1s\beta(r’)|\) determinant, when written as
\[|1s\alpha(r) 1s\beta(r’)| = \frac{1}{\sqrt{2}}\{1s\alpha(r) 1s\beta(r’) - 1s\alpha(r’) 1s\beta(r)\} \]
can be multiplied by itself to produce the 2-electron spin- and spatial- probability density:
\[P(r, r’) = \frac{1}{2}\{[1s\alpha(r) 1s\beta(r’)]^2 + [1s\alpha(r’) 1s\beta(r)]^2 -1s\alpha(r) 1s\beta(r’) 1s\alpha(r’) 1s\beta(r) - 1s\alpha(r’) 1s\beta(r) 1s\alpha(r) 1s\beta(r’)\}.\]
If we now integrate over the spins of the two electrons and make use of
\[\langle a|a \rangle = \langle b|b \rangle = 1 \label{6.1.1a}\]
and
\[\langle a|b \rangle = \langle b|a\rangle = 0 \label{6.1.1b}\]
we obtain the following spatial (i.e., with spin absent) probability density:
\[P(r,r’) = |1s(r)|^2 |1s(r’)|^2. \]
This probability, being a product of the probability density for finding one electron at r times the density of finding another electron at \(r’\), clearly has no correlation in it. That is, the probability of finding one electron at r does not depend on where \((r’)\) the other electron is. This product form for \(P(r,r’)\) is a direct result of the single-determinant form for y, so this form must be wrong if electron correlation is to be accounted for.
Electron Correlation
Now, we need to ask how \(\psi\) should be written if electron correlation effects are to be taken into account. As we now demonstrate, it turns out that one can account for electron avoidance by taking \(\psi\) to be a combination of two or more determinants that differ by the promotion of two electrons from one orbital to another orbital. For example, in describing the \(\pi^2\) bonding electron pair of an olefin or the \(ns^2\) electron pair in alkaline earth atoms, one mixes in doubly excited determinants of the form \((\pi^*)^2\) or \(np^2\), respectively.
Briefly, the physical importance of such doubly-excited determinants can be made clear by using the following identity involving determinants:
\[C_1 | ..\phi_\alpha \phi_\beta..| - C_2 | ..\phi'_\alpha \phi'_\beta..|\]
\[= \dfrac{C_1}{2} { | ..( \phi - x\phi')\alpha ( \phi + x\phi')b..| - | ..( \phi - x\phi')\beta ( \phi + x\phi')\alpha..| },\]
where
\[x = \sqrt{\dfrac{C_2}{C_1}} .\]
This identity is important to understand, so please make sure you can work through the algebra needed to prove it. It allows one to interpret the combination of two determinants that differ from one another by a double promotion from one orbital \((\phi)\) to another \((\phi')\) as equivalent to a singlet coupling (i.e., having \(\alpha\beta-\beta\alpha\) spin function) of two different orbitals \((\phi - x\phi')\) and \((\phi + x\phi')\) that comprise what are called polarized orbital pairs. In the simplest embodiment of such a configuration interaction (CI) description of electron correlation, each electron pair in the atom or molecule is correlated by mixing in a configuration state function (CSF) in which that electron pair is doubly excited to a correlating orbital. A CSF is the minimum combination of determinants needed to express the proper spin eigenfunction for a given orbital occupation.
In the olefin example mentioned above, the two non-orthogonal polarized orbital pairs involve mixing the p and p* orbitals to produce two left-right polarized orbitals as depicted in Figure 6.1.9:
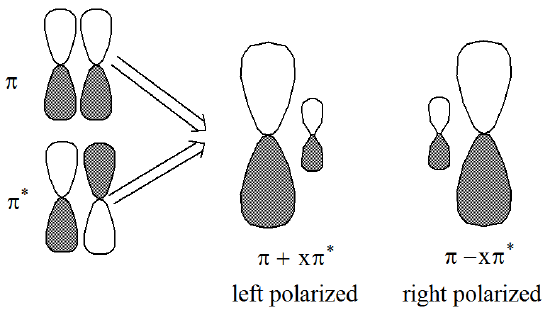
In this case, one says that the \(\pi^2\) electron pair undergoes left-right correlation when the \((\pi^*)^2\) determinant is mixed into the CI wavefunction.
In the alkaline earth atom case, the polarized orbital pairs are formed by mixing the \(ns\) and \(np\) orbitals (actually, one must mix in equal amounts of \(p_x, p_y\), and \(p_z\) orbitals to preserve overall \(^1S\) symmetry in this case), and give rise to angular correlation of the electron pair. Such a pair of polarized orbitals is shown in Figure 6.1.10.
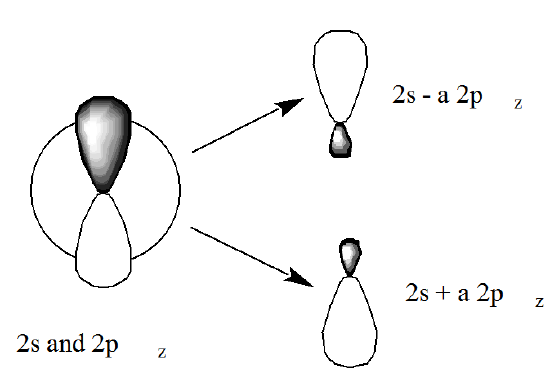
More specifically, the following four determinants are found to have the largest amplitudes in \(\psi\) for Be:
\[\psi \cong C_1 |1s^22s^2 | - C_2 [|1s^22p_x^2 | +|1s^22p_y^2 | +|1s^22p_z^2 |].\]
The fact that the latter three terms possess the same amplitude \(C_2\) is a result of the requirement that a state of \(^1S\) symmetry is desired. It can be shown that this function is equivalent to:
\[\psi \cong \frac{1}{6} C_1 |1s\alpha1s\beta [[(2s-a2p_x)\alpha(2s+a2p_x)\beta - (2s-a2p_x)\beta(2s+a2p_x)\alpha]\\
+[(2s-a2p_y)\alpha(2s+a2p_y)\beta - (2s-a2p_y)\beta(2s+a2p_y)\alpha]\\
+[(2s-a2p_z)\alpha(2s+a2p_z)\beta - (2s-a2p_z)\beta(2s+a2p_z)\alpha] ] |,\]
where \(a = \sqrt{3C_2/C_1}\).
Here two electrons occupy the \(1s\) orbital (with opposite, \(\alpha\) and \(\beta\) spins), and are thus not being treated in a correlated manner, while the other pair resides in \(2s\)/\(2p\) polarized orbitals in a manner that instantaneously correlates their motions. These polarized orbital pairs \((2s ± a 2p_{x,y,\text{ or }z})\) are formed by combining the \(2s\) orbital with the \(2p_{x,y,\text{ or }z}\) orbital in a ratio determined by \(C_2/C_1\).
This ratio \(C_2/C_1\) can be shown using perturbation theory to be proportional to the magnitude of the coupling \(\langle 1s^22s^2 |H|1s^22p^2 \rangle\) matrix element between the two configurations involved and inversely proportional to the energy difference
\([\langle 1s^22s^2H|1s^22s^2 \rangle - \langle 1s^22p^2|H|1s^22p^2 \rangle]\)
between these configurations. In general, configurations that have similar Hamiltonian expectation values and that are coupled strongly give rise to strongly mixed (i.e., with large \(|C_2/C_1|\) ratios) polarized orbital pairs.
II.Later in this Chapter, you will learn how to evaluate Hamiltonian matrix elements between pairs of antisymmetric wavefunctions. If you are anxious to learn this now, go to the subsection entitled The Slater-Condon Rules and read that before returning here.
In each of the three equivalent terms in the alkaline earth wavefunction, one of the valence electrons moves in a \(2s+a2p\) orbital polarized in one direction while the other valence electron moves in the \(2s-a2p\) orbital polarized in the opposite direction. For example, the first term
\([(2s-a2p_x)\alpha(2s+a2p_x)\beta - (2s-a2p_x)\beta(2s+a2p_x)\alpha]\)
describes one electron occupying a \(2s-a2p_x\) polarized orbital while the other electron occupies the \(2s+a2p_x\) orbital. The electrons thus reduce their Coulomb repulsion by occupying different regions of space; in the SCF picture \(1s^22s^2\), both electrons reside in the same \(2s\) region of space. In this particular example, the electrons undergo angular correlation to avoid one another.
The use of doubly excited determinants is thus seen as a mechanism by which \(\psi\) can place electron pairs, which in the single-configuration picture occupy the same orbital, into different regions of space (i.e., each one into a different member of the polarized orbital pair) thereby lowering their mutual Coulomb repulsion. Such electron correlation effects are extremely important to include if one expects to achieve chemically meaningful accuracy (i.e., ± 5 kcal/mole).
Essential Configuration Interaction
There are occasions in which the inclusion of two or more determinants in \(\psi\) is essential to obtaining even a qualitatively correct description of the molecule’s electronic structure. In such cases, we say that we are including essential correlation effects. To illustrate, let us consider the description of the two electrons in a single covalent bond between two atoms or fragments that we label X and Y. The fragment orbitals from which the bonding \(\sigma\) and antibonding \(\sigma^*\) MOs are formed we will label \(s_X\) and \(s_Y\), respectively.
Several spin- and spatial- symmetry adapted 2-electron determinants (i.e., CSFs) can be formed by placing two electrons into the \(\sigma\) and \(\sigma^*\) orbitals. For example, to describe the singlet determinant corresponding to the closed-shell \(\sigma^2\) orbital occupancy, a single Slater determinant
\[^1\Sigma (0) = |\sigma\alpha \sigma\beta| = \frac{1}{\sqrt{2}} [\sigma\alpha(1)\sigma\beta(2) - \sigma\beta(1)\sigma\alpha(2) ]\]
suffices. An analogous expression for the \((\sigma^*)^2\) determinant is given by
\[{}^1\Sigma^{**} (0) = | \sigma^*\alpha \sigma^*\beta | = \frac{1}{\sqrt{2}} [ \sigma^*\alpha(1) \sigma^*\beta(2) - \sigma^*\alpha(2) \sigma^*\beta(1) ]\]
Also, the \(M_S = 1\) component of the triplet state having \(\sigma\sigma^*\) orbital occupancy can be written as a single Slater determinant:
\[{}^3\Sigma^{*} (1) = |\sigma\alpha \sigma^*\alpha | = \frac{1}{\sqrt{2}} [\sigma\alpha(1) \sigma^*\alpha(2) - \sigma^*\alpha(1)\sigma\alpha(2) ],\]
as can the \(M_S = -1\) component of the triplet state
\[{}^3\Sigma^{*}(-1) = |\sigma\beta \sigma^*\beta | = \frac{1}{\sqrt{2}} [\sigma\beta(1) \sigma^*\beta(2) - \sigma^*\beta(1)\sigma\beta(2) ].\]
However, to describe the singlet and \(M_S = 0\) triplet states belonging to the \(\sigma\sigma^*\) occupancy, two determinants are needed:
\[ {}^1\Sigma^{*} (0) = \frac{1}{\sqrt{2}} [\sigma\alpha \sigma^*\beta - \sigma\beta\sigma^*\alpha ]\]
is the singlet and
\[ {}^3\Sigma^{*}(0) = \frac{1}{\sqrt{2}} [\sigma\alpha \sigma^*\beta + \sigma\beta\sigma^*\alpha ] \]
is the triplet (note, you can obtain this \(M_S = 0\) triplet by applying \(\textbf{S}_- = \textbf{S}_- (1) + \textbf{S}_- (2)\) to the \(M_S = 1\) triplet). In each case, the spin quantum number \(S\), its z-axis projection \(M_S\), and the \(L\) quantum number are given in the conventional \(^{2S+1}\Lambda(M_S)\) term symbol notation.
As the distance \(R\) between the X and Y fragments is changed from near its equilibrium value of \(R_e\) and approaches infinity, the energies of the \(\sigma\) and \(\sigma^*\) orbitals vary in a manner well known to chemists as depicted in Figure 6.1.11 if X and Y are identical.
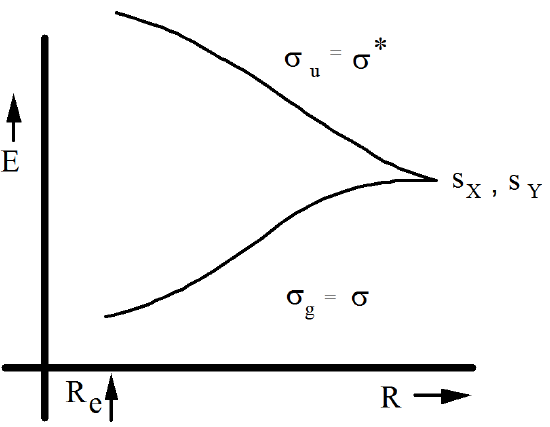
If X and Y are not identical, the \(s_x\) and \(s_y\) orbitals still combine to form a bonding \(\sigma\) and an antibonding \(\sigma^*\) orbital. The energies of these orbitals, for R values ranging from near \(R_e\) to \(R\rightarrow \infty\), are depicted in Figure 6.1.12 for the case in which X is more electronegative than Y.
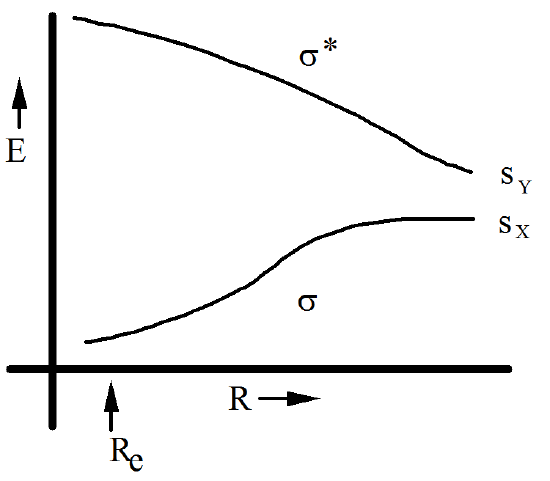
The energy variation in these orbital energies gives rise to variations in the energies of the six determinants listed above. As \(R \rightarrow \infty\), the determinants’ energies are difficult to intuit because the \(\sigma\) and \(\sigma^*\) orbitals become degenerate (in the homonuclear case) or nearly so (in the \(X \ne Y\) case). To pursue this point and arrive at an energy ordering for the determinants that is appropriate to the \(R \rightarrow \infty\) region, it is useful to express each such function in terms of the fragment orbitals \(s_x \) and \(s_y\) that comprise \(\sigma\) and \(\sigma^*\). To do so, the LCAO-MO expressions for \(\sigma\) and \(\sigma^*\),
\[\sigma = C [s_x + z s_y]\]
and
\[\sigma^* = C^* [z s_x - s_y],\]
are substituted into the Slater determinant definitions given above. Here \(C\) and \(C^*\) are the normalization constants. The parameter \(z\) is 1.0 in the homonuclear case and deviates from 1.0 in relation to the \(s_x\) and \(s_y\) orbital energy difference (if \(s_x\) lies below \(s_y\), then \(z < 1.0\); if \(s_x\) lies above \(s_y\), \(z > 1.0\)).
Let us examine the \(X=Y\) case to keep the analysis as simple as possible. The process of substituting the above expressions for \(\sigma\) and \(\sigma^*\) into the Slater determinants that define the singlet and triplet functions can be illustrated as follows for the \(^1\Sigma(0)\) case:
\[{}^1\Sigma(0) = |\sigma\alpha \sigma\beta| = C_2 | (s_x + s_y) \alpha(s_x + s_y) \beta| \]
\[= C_2 [|s_x \alpha s_x b| + |s_y \alpha s_y \beta| + |s_x \alpha s_y \beta| + |s_y \alpha s_x \beta|] \]
The first two of these atomic-orbital-based Slater determinants (\(|s_x \alpha s_x b|\) and \(|s_y \alpha s_y \beta|\)) are called ionic because they describe atomic orbital occupancies, which are appropriate to the \(R \rightarrow \infty\) region that correspond to \(X \bullet\bullet + X \) and \(X + X \bullet\bullet\) valence bond structures, while \(|s_x \alpha s_y \beta|\) and \(|s_y \alpha s_x \beta|\) are called "covalent" because they correspond to \(X\bullet + X\bullet\) structures.
In similar fashion, the remaining five determinant functions may be expressed in terms of fragment-orbital-based Slater determinants. In so doing, use is made of the antisymmetry of the Slater determinants (e.g., \(| \phi_1 \phi_2 \phi_3 | = - | \phi_1 \phi_3 \phi_2 |\)), which implies that any determinant in which two or more spin-orbitals are identical vanishes \(| \phi_1 \phi_2 \phi_2 | = - | \phi_1 \phi_2 \phi_2 | = 0\). The result of decomposing the MO-based determinants into their fragment-orbital components is as follows:
\[ {}^1\Sigma^{**} (0) = |\sigma^*\alpha \sigma^*\beta | = C^*{}^2 [ |s_x \alpha s_x \beta| + |s_y \alpha s_y \beta| - |s_x \alpha s_y \beta| - |s_y \alpha s_x \beta|]\]
\[ {}^1\Sigma^{*} (0) =\frac{1}{\sqrt{2}}[ |\sigma\alpha \sigma^*\beta | - |\sigma\beta \sigma^*\alpha | ]= CC^* \sqrt{2} [|s_x \alpha s_x \beta| - |s_y \alpha s_y \beta|] \]
\[ {}^3\Sigma^{*} (1) = |\sigma\alpha \sigma^*\alpha | = CC^* 2|s_y \alpha s_x \alpha|\]
\[ {}^3\Sigma^{*} (0) = \frac{1}{\sqrt{2}}[ \sigma\alpha \sigma^*\beta | + |\sigma\beta \sigma^*\alpha |]=CC^* \sqrt{2} [|s_y \alpha s_x \beta| - |s_x \alpha s_y \beta|]\]
\[ {}^3\Sigma^{*} (-1) = |\sigma\alpha \sigma^*\alpha | = CC^* 2|s_y \beta s_x \beta|\]
These decompositions of the six valence determinants into fragment-orbital or valence bond components allow the \(R = \infty\) energies of these states to specified. For example, the fact that both \({}^1\Sigma\) and \({}^1\Sigma^{**}\) contain 50% ionic and 50% covalent structures implies that, as \(R \rightarrow \infty\), both of their energies will approach the average of the covalent and ionic atomic energies \(\frac{1}{2} [E (X\bullet ) + E (X\bullet ) + E (X) + E ( X \bullet\bullet) ]\). The \({}^1\Sigma^{*}\) energy approaches the purely ionic value \(E (X)+ E (X \bullet\bullet )\) as \(R \rightarrow \infty\). The energies of \({}^3\Sigma^{*}(0), {}^3\Sigma^{*}(1)\) and \({}^3\Sigma^{*}(-1)\) all approach the purely covalent value \(E (X\bullet ) + E (X\bullet )\) as \(R \rightarrow \infty\).
The behaviors of the energies of the six valence determinants as \(R\) varies are depicted in Figure 6.1.13 for situations in which the homolytic bond cleavage is energetically favored (i.e., for which \(E (X\bullet ) + E (X\bullet ) < E (X) +E ( X \bullet\bullet)\)).
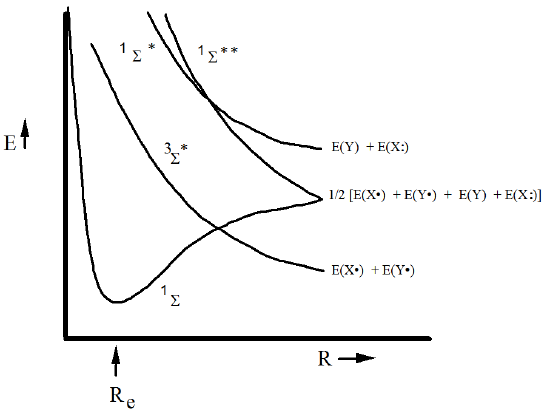
It is essential to realize that the energies of the determinants do not represent the energies of the true electronic states. For \(R\)-values at which the determinant energies are separated widely, the true state energies are rather well approximated by individual determinant energies; such is the case near Re for the \({}^1\Sigma\) state.
However, at large \(R\), the situation is very different, and it is in such cases that what we term essential configuration interaction occurs. Specifically, for the \(X=Y\) example, the \({}^1\Sigma\) and \({}^1\Sigma^{**}\) determinants undergo essential CI coupling to form a pair of states of \({}^1\Sigma\) symmetry (the \({}^1\Sigma^{*}\) CSF cannot partake in this CI mixing because it is of ungerade symmetry; the \({}^3\Sigma^{*}\) states can not mix because they are of triplet spin symmetry). The CI mixing of the \({}^1\Sigma\) and \({}^1\Sigma^{**}\) determinants is described in terms of a 2x2 secular problem
\[ \left[\begin{array}{cc}
\langle ^1\Sigma | H | ^1\Sigma \rangle & \langle ^1\Sigma | H | ^1\Sigma^{**} \rangle \\
\langle ^1\Sigma^{**} | H | ^1\Sigma \rangle & \langle ^1\Sigma^{**} | H | ^1\Sigma^{**} \rangle
\end{array}\right]
\left[\begin{array}{c}A\\B\end{array}\right]
= E\left[\begin{array}{c}A\\B\end{array}\right] \]
The diagonal entries are the determinants’ energies depicted in Figure 6.1.13. The off-diagonal coupling matrix elements can be expressed in terms of an exchange integral between the \(\sigma\) and \(\sigma^*\) orbitals:
\[\langle {}^1\Sigma|H|{}^1\Sigma^{**} \rangle = \langle |\sigma\alpha \sigma\beta|H||\sigma^*\alpha \sigma^*\beta |\rangle = \langle \sigma\sigma|| \sigma^*\sigma^* \rangle = K_{\sigma \sigma^*}\]
Later in this Chapter, you will learn how to evaluate Hamiltonian matrix elements between pairs of antisymmetric wavefunctions and to express them in terms of one- and two-electron integrals. If you are anxious to learn this now, go to the subsection entitled the Slater-Condon Rules and read that before returning here.
At \(R \rightarrow \infty\), where the \({}^1\Sigma\) and \({}^1\Sigma^{**}\) determinants are degenerate, the two solutions to the above CI matrix eigenvalue problem are:
\[ E =\frac{1}{2} [ E (X\bullet ) + E (X\bullet ) + E (X)+ E (X \bullet\bullet) ] \mp \langle \sigma\sigma | \frac{1}{r_{12}} | \sigma^* \sigma^*\rangle \]
with respective amplitudes for the \({}^1\Sigma\) and \({}^1\Sigma^{**}\) CSFs given by
\[ A_\mp = \pm \frac{1}{\sqrt{2}} ; \hspace{15pt} B_{\mp} = \mp \frac{1}{\sqrt{2}}.\]
The first solution thus has
\[ \psi_{-} = \frac{1}{\sqrt{2}} [|\sigma\alpha \sigma\beta| - |\sigma^*\alpha \sigma^*\beta |]\]
which, when decomposed into atomic orbital components, yields
\[\psi_{-} = \frac{1}{\sqrt{2}} [ |s_x\alpha s_y\beta| - |s_x\beta s_y\alpha|].\]
The other root has
\[ \psi_{+} = \frac{1}{\sqrt{2}} [|\sigma\alpha \sigma\beta| + |\sigma^*\alpha \sigma^*\beta |] = \frac{1}{\sqrt{2}} [ |s_x\alpha s_x\beta| + |s_y a s_y\beta|].\]
So, we see that \({}^1\Sigma\) and \({}^1\Sigma^{**}\), which both contain 50% ionic and 50% covalent parts, combine to produce \(\psi_{-}\) which is purely covalent and \(\psi_{+}\) which is purely ionic.
The above essential CI mixing of \({}^1\Sigma\) and \({}^1\Sigma^{**}\) as \(R \rightarrow \infty\) qualitatively alters the energy diagrams shown above. Descriptions of the resulting valence singlet and triplet S states are given in Figure 6.1.14 for homonuclear situations in which covalent products lie below the ionic fragments.
Figure 6.1.14: State Correlation Diagram Showing How the Energies of the States, Comprised of Combinations of Determinants, vary with \(R\).


