4.4: Point Group Symmetry
- Page ID
- 11582
It is assumed that the reader has previously learned how symmetry arises in molecular shapes and structures and what symmetry elements are (e.g., planes, axes of rotation, centers of inversion, etc.). We review and teach here only that material that is of direct application to symmetry analysis of molecular orbitals and vibrations and rotations of molecules. We use a specific example, the ammonia molecule, to introduce and illustrate the important aspects of point group symmetry because this example contains most of the complexities that arise in any application of group theory to molecular problems.
Example \(\PageIndex{1}\): The \(C_{3v}\) Symmetry Group of Ammonia
The ammonia molecule \(NH_3\) belongs, in its ground-state equilibrium geometry, to the \(C_{3v}\) point group. Its symmetry operations consist of two \(C_3\) rotations, \(C_3\), \(C_3^2\) (rotations by 120° and 240°, respectively about an axis passing through the nitrogen atom and lying perpendicular to the plane formed by the three hydrogen atoms), three vertical reflection operations, \(\sigma_v\), \(\sigma_{v'}\), \(\sigma_{v"}\), and the identity operation. Corresponding to these six operations are symmetry elements: the three-fold rotation axis, \(C_3\) and the three symmetry planes \(\sigma_v\), \(\sigma_{v'}\) and \(\sigma_{v"}\) that contain the three \(NH\) bonds and the \(z\)-axis (see Figure 4.3).
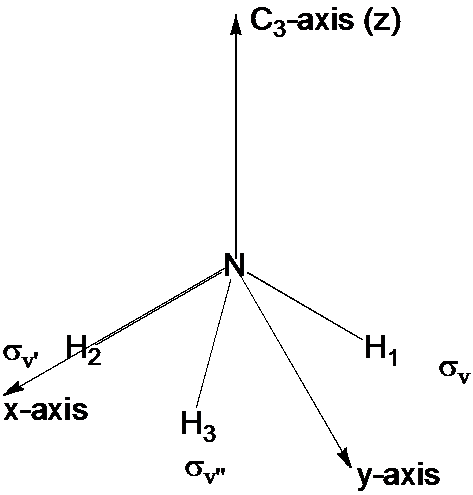
These six symmetry operations form a mathematical group. A group is defined as a set of objects satisfying four properties.
- A combination rule is defined through which two group elements are combined to give a result that we call the product. The product of two elements in the group must also be a member of the group (i.e., the group is closed under the combination rule).
- One special member of the group, when combined with any other member of the group, must leave the group member unchanged (i.e., the group contains an identity element).
- Every group member must have a reciprocal in the group. When any group member is combined with its reciprocal, the product is the identity element.
- The associative law must hold when combining three group members (i.e., (AB)C must equal A(BC)).
The members of symmetry groups are symmetry operations; the combination rule is successive operation. The identity element is the operation of doing nothing at all. The group properties can be demonstrated by forming a multiplication table. Let us label the rows of the table by the first operation and the columns by the second operation. Note that this order is important because most groups are not commutative. The \(C_{3v}\) group multiplication table is as follows:
\[\begin{array}{c|p{1.3cm}p{1.3cm}p{1.3cm}p{1.3cm}p{1.3cm}p{1.3cm}p{1.3cm}p{1.3cm}c}
&E&C_3&C_3^2&\sigma_v&\sigma_{v'}&\sigma_{v"}&\text{Second Operation}\\\hline
C_3&C_3&C_3^2&E&\sigma_{v'}&\sigma_{v''}&\sigma_{v}&\\
C_3^2&C_3^2&E&C_3&\sigma_{v''}&\sigma_{v}&\sigma_{v'}&\\
\sigma_{v}&\sigma_{v}&\sigma_{v''}&\sigma_{v'}&E&C_3^2&C_3&\\
\sigma_{v'}&\sigma_{v'}&\sigma_{v}&\sigma_{v''}&C_3&E&C_3^2&\\
\sigma_{v''}&\sigma_{v''}&\sigma_{v'}&\sigma_{v}&C_3^2&C_3&E&\\
\text{First}&&&&&&&&\\
\text{Operation}&&&&&&&&
\end{array}
\]
Note the reflection plane labels do not move. That is, although we start with \(H_1\) in the \(\sigma_v\) plane, \(H_2\) in \(\sigma_{v'}\), and \(H_3\) in \(\sigma_{v"}\), if \(H_1\) moves due to the first symmetry operation, \(\sigma_v\) remains fixed and a different H atom lies in the \(\sigma_v\) plane.
Matrices as Group Representations
In using symmetry to help simplify molecular orbital (mo) or vibration/rotation energy-level identifications, the following strategy is followed:
- A set of \(M\) objects belonging to the constituent atoms (or molecular fragments, in a more general case) is introduced. These objects are the orbitals of the individual atoms (or of the fragments) in the mo case; they are unit vectors along the Cartesian \(x\), \(y\), and \(z\) directions located on each of the atoms, and representing displacements along each of these directions, in the vibration/rotation case.
- Symmetry tools are used to combine these \(M\) objects into \(M\) new objects each of which belongs to a specific symmetry of the point group. Because the Hamiltonian (electronic in the mo case and vibration/rotation in the latter case) commutes with the symmetry operations of the point group, the matrix representation of H within the symmetry-adapted basis will be "block diagonal". That is, objects of different symmetry will not interact; only interactions among those of the same symmetry need be considered.
To illustrate such symmetry adaptation, consider symmetry adapting the \(2s\) orbital of \(N\) and the three \(1s\) orbitals of the three H atoms. We begin by determining how these orbitals transform under the symmetry operations of the \(C_{3v}\) point group. The act of each of the six symmetry operations on the four atomic orbitals can be denoted as follows:
\[(S_N,S_1,S_2,S_3) \overset{E}{\rightarrow} (S_N,S_1,S_2,S_3)\\
\hphantom{(S_N,S_1,S_2,S_3)} \overset{C_3}{\rightarrow} (S_N,S_3,S_1,S_2)\\
\hphantom{(S_N,S_1,S_2,S_3)} \overset{C_3^2}{\rightarrow} (S_N,S_2,S_3,S_1)\\
\hphantom{(S_N,S_1,S_2,S_3)} \overset{\sigma_v}{\rightarrow} (S_N,S_1,S_3,S_2)\\
\hphantom{(S_N,S_1,S_2,S_3)} \overset{\sigma_{v''}}{\rightarrow} (S_N,S_3,S_2,S_1)\\
\hphantom{(S_N,S_1,S_2,S_3)} \overset{\sigma_{v'}}{\rightarrow} (S_N,S_2,S_1,S_3)\]
Here we are using the active view that a \(C_3\) rotation rotates the molecule by 120°. The equivalent passive view is that the \(1s\) basis functions are rotated -120°. In the \(C_3\) rotation, \(S_3\) ends up where \(S_1\) began, \(S_1\), ends up where \(S_2\) began and \(S_2\) ends up where \(S_3\) began.
These transformations can be thought of in terms of a matrix multiplying a vector with elements \((S_N,S_1,S_2,S_3)\). For example, if \(D^{(4)}(C_3)\) is the representation matrix giving the \(C_3\) transformation, then the above action of \(C_3\) on the four basis orbitals can be expressed as:
\[D^{(4)}(C_3)
\left(\begin{array}{c}S_N\\S_1\\S_2\\S_3\end{array}\right)=
\left(\begin{array}{cccc}
1 & 0 & 0 & 0 \\
0 & 0 & 0 & 1 \\
0 & 1 & 0 & 0 \\
0 & 0 & 1 & 0 \end{array}\right)
\left(\begin{array}{c}S_N\\S_1\\S_2\\S_3\end{array}\right)=
\left(\begin{array}{c}S_N\\S_3\\S_1\\S_2\end{array}\right)
\]
We can likewise write matrix representations for each of the symmetry operations of the \(C_{3v}\) point group:
\[D^{(4)}(C_3^2) =
\left(\begin{array}{cccc}
1 & 0 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1 \\
0 & 1 & 0 & 0 \end{array}\right)
\hspace{30pt}
D^{(4)}(E) =
\left(\begin{array}{cccc}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1 \end{array}\right)
\]
\[D^{(4)}(\sigma_v) =
\left(\begin{array}{cccc}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 0 & 1 \\
0 & 0 & 1 & 0 \end{array}\right)
\hspace{30pt}
D^{(4)}(\sigma_{v'}) =
\left(\begin{array}{cccc}
1 & 0 & 0 & 0 \\
0 & 0 & 0 & 1 \\
0 & 0 & 1 & 0 \\
0 & 1 & 0 & 0 \end{array}\right)
\]
\[D^{(4)}(\sigma_{v"}) =
\left(\begin{array}{cccc}
1 & 0 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 0 & 1
\end{array}\right)
\]
It is easy to verify that a \(C_3\) rotation followed by a \(\sigma_v\) reflection is equivalent to a \(\sigma_{v'}\) reflection alone. In other words
\[\sigma_v C_3 = \sigma_{v'},\hspace{1cm}\text{or }\hspace{1cm}\begin{array}{ccc}&S_1&\\&&\\S_2&&S_3\end{array}\overset{C_3}{\rightarrow} \begin{array}{ccc}&S_3&\\&&\\S_1&&S_2\end{array}\overset{\sigma_v}{\rightarrow} \begin{array}{ccc}&S_3&\\&&\\S_2&&S_1\end{array}\]
Note that this same relationship is carried by the matrices:
\[D^{(4)}(\sigma_v)D^{(4)}(C_3) =
\left(\begin{array}{cccc}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 0 & 1 \\
0 & 0 & 1 & 0
\end{array}\right)
\left(\begin{array}{cccc}
1 & 0 & 0 & 0 \\
0 & 0 & 0 & 1 \\
0 & 1 & 0 & 0 \\
0 & 0 & 1 & 0
\end{array}\right)
=
\left(\begin{array}{cccc}
1 & 0 & 0 & 0 \\
0 & 0 & 0 & 1 \\
0 & 0 & 1 & 0 \\
0 & 1 & 0 & 0
\end{array}\right)
=D^{(4)}(\sigma_{v'})\]
Likewise we can verify that \(C_3(\sigma_v) = \sigma_{v"}\) directly and we can notice that the matrices also show the same identity:
\[D^{(4)}(C_3)D^{(4)}(\sigma_v) =
\left(\begin{array}{cccc}
1 & 0 & 0 & 0 \\
0 & 0 & 0 & 1 \\
0 & 1 & 0 & 0 \\
0 & 0 & 1 & 0
\end{array}\right)
\left(\begin{array}{cccc}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 0 & 1 \\
0 & 0 & 1 & 0
\end{array}\right)
=
\left(\begin{array}{cccc}
1 & 0 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 0 & 1
\end{array}\right)
=D^{(4)}(\sigma_{v"}).\]
In fact, one finds that the six matrices, \(D^{(4)}(R)\), when multiplied together in all 36 possible ways, obey the same multiplication table as did the six symmetry operations. We say the matrices form a representation of the group because the matrices have all the properties of the group.
Characters of Representations
One important property of a matrix is the sum of its diagonal elements which is called the trace of the matrix \(D\) and is denoted \(Tr(D)\):
\[Tr(D) = \sum_iD_{ii}=\chi .\]
So, \(\chi\) is called the trace or character of the matrix. In the above example
\[\chi (E) = 4\]
\[\chi (C_3) = \chi (C_3^2) = 1\]
\[\chi (\sigma_v) = \chi (\sigma_{v'}) = \chi (\sigma_{v"}) = 2.\]
The importance of the characters of the symmetry operations lies in the fact that they do not depend on the specific basis used to form the matrix. That is, they are invariant to a unitary or orthogonal transformation of the objects used to define the matrices. As a result, they contain information about the symmetry operation itself and about the space spanned by the set of objects. The significance of this observation for our symmetry adaptation process will become clear later.
Note that the characters of both rotations are the same as are the characters of all three reflections. Collections of operations having identical characters are called classes. Each operation in a class of operations has the same character as other members of the class. The character of a class depends on the space spanned by the basis of functions on which the symmetry operations act.
Another Basis and Another Representation
Above we used \((S_N,S_1,S_2,S_3)\) as a basis. If, alternatively, we use the one-dimensional basis consisting of the \(1s\) orbital on the N-atom, we obtain different characters, as we now demonstrate.
The act of the six symmetry operations on this \(S_N\) can be represented as follows:
\[S_N \overset{E}{\rightarrow} S_N \hspace{15pt} S_N \overset{C_3}{\rightarrow} S_N \hspace{15pt} S_N \overset{C_3^2}{\rightarrow} S_N;\]
\[S_N \overset{\sigma_v}{\rightarrow} S_N \hspace{15pt} S_N \overset{\sigma_{v''}}{\rightarrow} S_N \hspace{15pt} S_N \overset{\sigma_{v'}}{\rightarrow} S_N.\]
We can represent this group of operations in this basis by the one-dimensional set of matrices:
\[D^{(1)} (E) = 1; \hspace{15pt} D^{(1)}(C_3) = 1; \hspace{15pt} D^{(1)}(C_3^2) = 1,\]
\[D^{(1)} (\sigma_v) = 1; \hspace{15pt} D^{(1)}(\sigma_{v"}) = 1; \hspace{15pt} D^{(1)}(\sigma_{v'}) = 1.\]
Again we have
\[D^{(1)} (\sigma_v) D^{(1)}(C_3) = 1 \oplus 1 = D^{(1)}(\sigma_{v"}),\text{ and}\]
\[D^{(1)} (C_3) (D^{(1)}(\sigma_v) = 1 \oplus 1 = D^{(1)}(\sigma_{v'}).\]
These six 1x1 matrices form another representation of the group. In this basis, each character is equal to unity. The representation formed by allowing the six symmetry operations to act on the \(1s\) N-atom orbital is clearly not the same as that formed when the same six operations acted on the \((S_N,S_1,S_2,S_3)\) basis. We now need to learn how to further analyze the information content of a specific representation of the group formed when the symmetry operations act on any specific set of objects.
Reducible and Irreducible Representations
Reducible Representations
Note that every matrix in the four dimensional group representation labeled \(D^{(4)}\) has the so-called block diagonal form
\[
\begin{array}{|c|ccc|}\hline
1 &0 & 0 & 0\\\hline
0 & A & B & C \\
0 & D & E & F \\
0 & G & H & I \\\hline
\end{array}
\]
This means that these \(D^{(4)}\) matrices are really a combination of two separate group representations (mathematically, it is called a direct sum representation). We say that \(D^{(4)}\) is reducible into a one-dimensional representation \(D^{(1)}\) and a three-dimensional representation formed by the 3x3 submatrices that we will call \(D^{(3)}\).
\[D^{(3)}(E) =
\left(\begin{array}{ccc}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}\right)
\hspace{20pt}
D^{(3)}(C_3) =
\left(\begin{array}{ccc}
0 & 0 & 1 \\
1 & 0 & 0 \\
0 & 1 & 0
\end{array}\right)
\hspace{20pt}
D^{(3)}(C_3^2) =
\left(\begin{array}{ccc}
0 & 1 & 0 \\
0 & 0 & 1 \\
1 & 0 & 0
\end{array}\right)
\]
\[D^{(3)}(\sigma_v) =
\left(\begin{array}{ccc}
1 & 0 & 0 \\
0 & 0 & 1 \\
0 & 1 & 0
\end{array}\right)
\hspace{20pt}
D^{(3)}(\sigma_{v'}) =
\left(\begin{array}{ccc}
0 & 0 & 1 \\
0 & 1 & 0 \\
1 & 0 & 0
\end{array}\right)
\hspace{20pt}
D^{(3)}(\sigma_{v"}) =
\left(\begin{array}{ccc}
0 & 1 & 0 \\
1 & 0 & 0 \\
0 & 0 & 1
\end{array}\right)
\]
The characters of \(D^{(3)}\) are \(\chi (E) = 3, \chi (2C_3) = 0, \chi (3\sigma_v) = 1\). Note that we would have obtained this \(D^{(3)}\) representation directly if we had originally chosen to examine the basis \((S_1,S_2,S_3)\) alone; also note that these characters are equal to those of \(D^{(4)}\) minus those of \(D^{(1)}\).
Change in Basis
Now let us convert to a new basis that is a linear combination of the original \(S_1,S_2,S_3\) basis:
\[T_1 = S_1 + S_2 + S_3\]
\[T_2 = 2S_1 - S_2 - S_3\]
\[T_3 = S_2 - S_3\]
(Don't worry about how I constructed \(T_1\), \(T_2\), and \(T_3\) yet. As will be demonstrated later, we form them by using symmetry projection operators defined below). We determine how the \("T"\) basis functions behave under the group operations by allowing the operations to act on the \(S_j\) and interpreting the results in terms of the \(T_i\). In particular,
\[(T_1,T_2 ,T_3) \overset{\sigma_v}{\rightarrow} (T_1,T_2,-T_3) \hspace{15pt} (T_1,T_2,T_3) \overset{E}{\rightarrow} (T_1,T_2,T_3) ;\]
\[(T_1,T_2,T_3) \overset{\sigma_{v'}}{\rightarrow} (S_3+S_2+S_1, 2S_3-S_2-S_1,S_2-S_1) = (T_1, -\frac{1}{2} T_2 – \frac{3}{2} T_3, - \frac{1}{2} T_2 + \frac{1}{2} T_3);\]
\[(T_1,T_2,T_3) \overset{\sigma_{v''}}{\rightarrow} (S_2+S_1+S_3, 2S_2-S_1-S_3,S_1-S_3) = (T_1, - \frac{1}{2} T_2 + \frac{3}{2} T_3, \frac{1}{2}T_2 + \frac{1}{2}T_3);\]
\[(T_1,T_2,T_3) \overset{C_3}{\rightarrow} (S_3+S_1+S_2, 2S_3-S_1-S_2,S_1-S_2) = (T_1, - \frac{1}{2}T_2 – \frac{3}{2}T_3, \frac{1}{2}T_2 – \frac{1}{2}T_3);\]
\[(T_1,T_2,T_3) \overset{C_3^2}{\rightarrow} (S_2+S_3+S_1, 2S_2-S_3-S_1,S_3-S_1) = (T_1, - \frac{1}{2}T_2 + \frac{3}{2}T_3, - \frac{1}{2}T_2 – \frac{1}{2}T_3).\]
So the matrix representations in the new \(T_i\) basis are:
\[D^{(3)}(E) =
\left(\begin{array}{ccc}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}\right)
\hspace{20pt}
D^{(3)}(C_3) =
\left(\begin{array}{ccc}
1 & 0 & 0 \\
0 & -\frac{1}{2} & -\frac{3}{2} \\
0 & \frac{1}{2} & -\frac{1}{2}
\end{array}\right)
;\]
\[D^{(3)}(C_3^2) =
\left(\begin{array}{ccc}
1 & 0 & 0 \\
0 & -\frac{1}{2} & \frac{3}{2} \\
0 & -\frac{1}{2} & -\frac{1}{2}
\end{array}\right)
\hspace{20pt}
D^{(3)}(\sigma_v) =
\left(\begin{array}{ccc}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & -1
\end{array}\right)
;\]
\[D^{(3)}(\sigma_{v'}) =
\left(\begin{array}{ccc}
1 & 0 & 0 \\
0 & -\frac{1}{2} & -\frac{3}{2} \\
0 & -\frac{1}{2} & \frac{1}{2}
\end{array}\right)
\hspace{20pt}
D^{(3)}(\sigma_{v"}) =
\left(\begin{array}{ccc}
1 & 0 & 0 \\
0 & -\frac{1}{2} & \frac{3}{2} \\
0 & \frac{1}{2} & \frac{1}{2}
\end{array}\right)
\]
Reduction of the Reducible Representation
These six matrices can be verified to multiply just as the symmetry operations do; thus they form another three-dimensional representation of the group. We see that in the \(T_i\) basis the matrices are block diagonal. This means that the space spanned by the \(T_i\) functions, which is the same space as the \(S_j\) span, forms a reducible representation that can be decomposed into a one dimensional space and a two dimensional space (via formation of the \(T_i\) functions). Note that the characters (traces) of the matrices are not changed by the change in bases.
The one-dimensional part of the above reducible three-dimensional representation is seen to be the same as the totally symmetric representation we arrived at before, \(D^{(1)}\). The two-dimensional representation that is left can be shown to be irreducible; it has the following matrix representations:
\[D^{(2)}(E) =
\left(\begin{array}{cc}
1 & 0 \\
0 & 1
\end{array}\right)
\hspace{15pt}
D^{(2)}(C_3) =
\left(\begin{array}{cc}
-\frac{1}{2} & -\frac{3}{2} \\
\frac{1}{2} & -\frac{1}{2}
\end{array}\right)
\hspace{15pt}
D^{(2)}(C_3^2) =
\left(\begin{array}{cc}
-\frac{1}{2} & \frac{3}{2} \\
-\frac{1}{2} & -\frac{1}{2}
\end{array}\right)
\]
\[D^{(2)}(\sigma_v) =
\left(\begin{array}{cc}
1 & 0 \\
0 & -1
\end{array}\right)
\hspace{15pt}
D^{(2)}(\sigma_{v'}) =
\left(\begin{array}{cc}
-\frac{1}{2} & -\frac{3}{2} \\
-\frac{1}{2} & \frac{1}{2}
\end{array}\right)
\hspace{15pt}
D^{(2)}(\sigma_{v'}') =
\left(\begin{array}{cc}
-\frac{1}{2} & -\frac{3}{2} \\
-\frac{1}{2} & \frac{1}{2}
\end{array}\right)
\]
The characters can be obtained by summing diagonal elements:
\[\chi (E) = 2, \chi (2C_3) = -1, \chi (3\sigma_v) = 0.\]
Rotations as a Basis
Another one-dimensional representation of the group can be obtained by taking rotation about the Z-axis (the \(C_3\) axis) as the object on which the symmetry operations act:
\[ R_z \overset{E}{\rightarrow} R_z \hspace{15pt} R_z \overset{C_3}{\rightarrow} R_z\hspace{15pt} R_z \overset{C_3^2}{\rightarrow} R_z;\]
\[ R_z \overset{\sigma_v}{\rightarrow} -R_z \hspace{15pt} R_z \overset{\sigma_{v''}}{\rightarrow} -R_z \hspace{15pt} R_z \overset{\sigma_{v'}}{\rightarrow} -R_z.\]
In writing these relations, we use the fact that reflection reverses the sense of a rotation. The matrix representations corresponding to this one-dimensional basis are:
\[D^{(1)}(E) = 1 \hspace{15pt} D^{(1)}(C_3) = 1 \hspace{15pt} D^{(1)}(C_3^2) = 1;\]
\[D^{(1)}(\sigma_v) = -1 \hspace{15pt} D^{(1)}(\sigma_{v"}) = -1 \hspace{15pt} D^{(1)} (\sigma_{v'}) = -1.\]
These one-dimensional matrices can be shown to multiply together just like the symmetry operations of the \(C_{3v}\) group. They form an irreducible representation of the group (because it is one-dimensional, it cannot be further reduced). Note that this one-dimensional representation is not identical to that found above for the \(1s\) N-atom orbital, or the \(T_1\) function.
Overview
We have found three distinct irreducible representations for the \(C_{3v}\) symmetry group; two different one-dimensional and one two dimensional representations. Are there any more? An important theorem of group theory shows that the number of irreducible representations of a group is equal to the number of classes. Since there are three classes of operation (i.e., E, \(C_3\) and \(\sigma_v\)), we have found all the irreducible representations of the \(C_{3v}\) point group. There are no more.
The irreducible representations have standard names; the first \(D^{(1)}\) (that arising from the \(T_1\) and \(1s_N\) orbitals) is called \(A_1\), the \(D^{(1)}\) arising from \(R_z\) is called \(A_2\) and \(D^{(2)}\) is called \(E\) (not to be confused with the identity operation E). We will see shortly where to find and identify these names.
Thus, our original \(D^{(4)}\) representation was a combination of two \(A_1\) representations and one \(E\) representation. We say that \(D^{(4)}\) is a direct sum representation: \(D^{(4)} = 2A_1 \oplus E\). A consequence is that the characters of the combination representation \(D^{(4)}\) can be obtained by adding the characters of its constituent irreducible representations.
\[
\begin{array}{cccc}
&E & 2C_3 & 3\sigma_v \\
A_1& 1 & 1 & 1 \\
A_1& 1 & 1 & 1 \\
E & 2 & -1 & 0 \\ \hline
2A_1 \oplus E & 4 & 1 & 2 \\
\end{array}
\]
Decompose Reducible Representations in General
Suppose you were given only the characters (4,1,2). How can you find out how many times \(A_1\), \(E\), and \(A_2\) appear when you reduce \(D^{(4)}\) to its irreducible parts? You want to find a linear combination of the characters of \(A_1\), \(A_2\) and \(E\) that add up (4,1,2). You can treat the characters of matrices as vectors and take the dot product of \(A_1\) with \(D^{(4)}\)
\[
\left(\begin{array}{cccccc}
1 & 1 & 1 & 1 & 1& 1\\
E & C_3 & C_3^2 & \sigma_v & \sigma_{v'} & \sigma_{v''}
\end{array}\right)
\left(\begin{array}{cc}
4 &E \\
1 & C_3 \\
1 & C_3^2 \\
2 & \sigma_v \\
2 & \sigma_{v'} \\
2 & \sigma_{v''}
\end{array}\right)
= 4 + 1 + 1 + 2 + 2 + 2 = 12.\]
The vector \((1,1,1,1,1,1)\) is not normalized; hence to obtain the component of \((4,1,1,2,2,2)\) along a unit vector in the \((1,1,1,1,1,1)\) direction, one must divide by the norm of \((1,1,1,1,1,1)\); this norm is 6. The result is that the reducible representation contains \(12/6 = 2A_1\) components. Analogous projections in the \(E\) and \(A_2\) directions give components of 1 and 0, respectively. In general, to determine the number \(n_\Gamma\) of times irreducible representation \(\Gamma\) appears in the reducible representation with characters \(\chi_{\rm red}\), one calculates
\[n\Gamma =\dfrac{1}{g}\sum_R\chi_\Gamma(R)\chi_{\rm red}(R) ,\]
where \(g\) is the order of the group (i.e.. the number of operations in the group; six in our example) and \(\chi_\Gamma(R)\) are the characters of the \(\Gamma^{\rm th}\) irreducible representation.
Commonly Used Bases
We could take any set of functions as a basis for a group representation. Commonly used sets include: Cartesian displacement coordinates \((x,y,z)\) located on the atoms of a polyatomic molecule (their symmetry treatment is equivalent to that involved in treating a set of p orbitals on the same atoms), quadratic functions such as d orbitals \(- xy,yz,xz,x^2-y^2,z^2,\) as well as rotations about the \(x\), \(y\) and \(z\) axes. The transformation properties of these very commonly used bases are listed in the character tables shown in Section 4.4.
Summary
The basic idea of symmetry analysis is that any basis of orbitals, displacements, rotations, etc. transforms either as one of the irreducible representations or as a direct sum (reducible) representation. Symmetry tools are used to first determine how the basis transforms under action of the symmetry operations. They are then used to decompose the resultant representations into their irreducible components.
More Examples
The 2p Orbitals of Nitrogen
For a function to transform according to a specific irreducible representation means that the function, when operated upon by a point-group symmetry operator, yields a linear combination of the functions that transform according to that irreducible representation. For example, a \(2p_z\) orbital (\(z\) is the \(C_3\) axis of \(NH_3\)) on the nitrogen atom belongs to the \(A_1\) representation because it yields unity times itself when \(C_3\), \(C_3^2\), \(\sigma_v\), \(\sigma_{v'}\), \(\sigma_{v"}\) or the identity operation act on it. The factor of 1 means that \(2p_z\) has \(A_1\) symmetry since the characters (the numbers listed opposite \(A_1\) and below \(E, 2C_3,\) and \(3\sigma_v\) in the \(C_{3v}\) character table shown in Section 4.4) of all six symmetry operations are 1 for the \(A_1\) irreducible representation.
The \(2p_x\) and \(2p_y\) orbitals on the nitrogen atom transform as the \(E\) representation since \(C_3\), \(C_3^2\), \(\sigma_v\), \(\sigma_{v'}\), \(\sigma_{v"}\) and the identity operation map \(2p_x\) and \(2p_y\) among one another. Specifically,
\[ C_3 \left(\begin{array}{c}2p_x \\2p_y \end{array}\right)
=
\left(\begin{array}{cc}
\cos 120^\circ & - \sin 120 ^\circ \\
\sin 120^\circ & \cos 120 ^\circ
\end{array}\right)
\left(\begin{array}{c}2p_x \\2p_y \end{array}\right)
\]
\[ C_3^2\left(\begin{array}{c}2p_x \\2p_y \end{array}\right)
=
\left(\begin{array}{cc}
\cos 240^\circ & - \sin 240 ^\circ \\
\sin 240^\circ & \cos 240 ^\circ
\end{array}\right)
\left(\begin{array}{c}2p_x \\2p_y \end{array}\right)
\]
\[ E \left(\begin{array}{c}2p_x \\2p_y \end{array}\right)
=
\left(\begin{array}{cc}
1 &0 \\
0 & 1
\end{array}\right)
\left(\begin{array}{c}2p_x \\2p_y \end{array}\right)
\]
\[ \sigma_v \left(\begin{array}{c}2p_x \\2p_y \end{array}\right)
=
\left(\begin{array}{cc}
-1 &0 \\
0 & 1
\end{array}\right)
\left(\begin{array}{c}2p_x \\2p_y \end{array}\right)
\]
\[ \sigma_{v'} \left(\begin{array}{c}2p_x \\2p_y \end{array}\right)
=
\left(\begin{array}{cc}
\frac{1}{2} &\frac{\sqrt{3}}{2} \\
\frac{\sqrt{3}}{2} & -\frac{1}{2}
\end{array}\right)
\left(\begin{array}{c}2p_x \\2p_y \end{array}\right)
\]
\[ \sigma_{v"}\left(\begin{array}{c}2p_x \\2p_y \end{array}\right)
=
\left(\begin{array}{cc}
\frac{1}{2} &-\frac{\sqrt{3}}{2} \\
-\frac{\sqrt{3}}{2} & -\frac{1}{2}
\end{array}\right)
\left(\begin{array}{c}2p_x \\2p_y \end{array}\right)
.\]
The 2x2 matrices, which indicate how each symmetry operation maps \(2p_x\) and \(2p_y\) into some combinations of \(2p_x\) and \(2p_y\), are the representation matrices (\(D^{(IR)}\)) for that particular operation and for this particular irreducible representation (IR). For example,
\[
\left(\begin{array}{cc}
\frac{1}{2} &\frac{\sqrt{3}}{2} \\
\frac{\sqrt{3}}{2} & -\frac{1}{2}
\end{array}\right)
= D^{(E)}(\sigma_{v'})\]
This set of matrices have the same characters as the \(D^{(2)}\) matrices obtained earlier when the \(T_i\) displacement vectors were analyzed, but the individual matrix elements are different because we used a different basis set (here \(2p_x\) and \(2p_y\) ; above it was \(T_2\) and \(T_3\)). This illustrates the invariance of the trace to the specific representation; the trace only depends on the space spanned, not on the specific manner in which it is spanned.
Short-Cut
A short-cut device exists for evaluating the trace of such representation matrices (that is, for computing the characters). The diagonal elements of the representation matrices are the projections along each orbital of the effect of the symmetry operation acting on that orbital. For example, a diagonal element of the \(C_3\) matrix is the component of \(C_32p_y\) along the \(2p_y\) direction. More rigorously, it
is \(\int 2p_y^*C_32p_y d\tau\). Thus, the character of the \(C_3\) matrix is the sum of \(\int 2p_y^*C_32p_y d\tau\) and \(\int 2p_x^*C_32p_x d\tau\). In general, the character \(\chi\) of any symmetry operation \(S\) can be computed by allowing \(S\) to operate on each orbital \(\phi_i\), then projecting \(S\phi_i\) along \(\phi_i\) (i.e., forming \(\int\phi_i^*S\phi_id\tau\), and summing these terms,
\[\sum_i\int\phi_i^*S\phi_id\tau= \chi(S).\]
If these rules are applied to the \(2p_x\) and \(2p_y\) orbitals of nitrogen within the \(C_{3v}\) point group, one obtains
\[\chi (E) = 2, \chi (C_3) = \chi (C_3^2) = -1, \chi (\sigma_v) = \chi (\sigma_{v"}) = \chi (\sigma_{v'}) = 0.\]
This set of characters is the same as \(D^{(2)}\) above and agrees with those of the \(E\) representation for the \(C_{3v}\) point group. Hence, \(2p_x\) and \(2p_y\) belong to or transform as the \(E\) representation. This is why \((x,y)\) is to the right of the row of characters for the \(E\) representation in the \(C_{3v}\) character table shown in Section 4.4. In similar fashion, the \(C_{3v}\) character table (please refer to this table now) states that \(d_{x^2−y^2}\) and \(d_{xy}\) orbitals on nitrogen transform as E, as do \(d_{xy}\) and \(d_{yz}\), but \(d_{z^2}\) transforms as \(A_1\).
Earlier, we considered in some detail how the three \(1s_H\) orbitals on the hydrogen atoms transform. Repeating this analysis using the short-cut rule just described, the traces (characters) of the 3 x 3 representation matrices are computed by allowing \(E, 2C_3,\) and \(3\sigma_v\) to operate on \(1s_{H_1}\), \(1s_{H_2}\), and \(1s_{H_3}\) and then computing the component of the resulting function along the original function. The resulting characters are \(\chi (E) = 3, \chi (C_3) = \chi (C_3^2) = 0,\) and \(\chi (\sigma_v) = \chi (\sigma_{v'}) = \chi (\sigma_{v"}) = 1\), in agreement with what we calculated before.
Using the orthogonality of characters taken as vectors we can reduce the above set of characters to \(A_1 + E\). Hence, we say that our orbital set of three \(1s_H\) orbitals forms a reducible representation consisting of the sum of \(A_1\) and \(E\) IR's. This means that the three \(1s_H\) orbitals can be combined to yield one orbital of \(A_1\) symmetry and a pair that transform according to the \(E\) representation.
Projector Operators: Symmetry Adapted Linear Combinations of Atomic Orbitals
To generate the above \(A_1\) and \(E\) symmetry-adapted orbitals, we make use of so-called symmetry projection operators \(P_E\) and \(P_{A_1}\). These operators are given in terms of linear combinations of products of characters times elementary symmetry operations as follows:
\[P_{A_1} =\sum_S\chi_A(S)S\]
\[P_E =\sum_S\chi_E(S)S,\]
where \(S\) ranges over \(C_3\), \(C_3^2\), \(\sigma_v\), \(\sigma_{v'}\) and \(\sigma_{v"}\) and the identity operation. The result of applying \(P_{A_1}\) to say \(1s_{H_1}\) is
\[P_{A_1} 1s_{H_1} = 1s_{H_1} + 1s_{H_2}+1s_{H_3}+1s_{H_2}+1s_{H_3}+1s_{H_1}\\
= 2(1s_{H_1}+1s_{H_2}+1s_{H_3}) = \phi_{A_1},\]
which is an (unnormalized) orbital having \(A_1\) symmetry. Clearly, this same \(\phi_{A_1}\) orbital would be generated by \(P_{A_1}\) acting on \(1s_{H_2}\) or \(1s_{H_3}\). Hence, only one \(A_1\) orbital exists. Likewise,
\[P_E1s_{H_1} = 2 ⋅1s_{H_1} -1s_{H_2} -1s_{H_3} ≡ \phi_{E,1}\]
which is one of the symmetry adapted orbitals having \(E\) symmetry. The other \(E\) orbital can be obtained by allowing \(P_E\) to act on \(1s_{H_2}\) or \(1s_{H_3}\):
\[P_E1s_{H_2} = 2 ⋅1s_{H_2} -1s_{H_1} -1s_{H_3} ≡ \phi_{E,2}\]
\[P_E1s_{H_3} = 2 ⋅1s_{H_3} -1s_{H_1} -1s_{H_2} = \phi_{E,3} .\]
It might seem as though three orbitals having \(E\) symmetry were generated, but only two of these are really independent functions. For example, \(\phi_{E,3}\) is related to \(\phi_{E,1}\) and \(\phi_{E,2}\) as follows:
\[\phi_{E,3} = -(\phi_{E,1} + \phi_{E,2}).\]
Thus, only \(\phi_{E,1}\) and \(\phi_{E,2}\) are needed to span the two-dimensional space of the \(E\) representation. If we include \(\phi_{E,1}\) in our set of orbitals and require our orbitals to be orthogonal, then we must find numbers \(a\) and \(b\) such that \(\phi'_E = a\phi_{E,2} + b\phi_{E,3}\) is orthogonal to \(\phi_{E,1}: = 0\). A straightforward calculation gives \(a = -b\) or \(\phi'_E = a (1s_{H_2} -1s_{H_3})\) which agrees with what we used earlier to construct the \(T_i\) functions in terms of the \(S_j\) functions.
Summary
Let us now summarize what we have learned thus far about point group symmetry. Any given set of atomic orbitals {\(\phi_i\)}, atom-centered displacements, or rotations can be used as a basis for the symmetry operations of the point group of the molecule. The characters \(\chi(S)\) belonging to the operations \(S\) of this point group within any such space can be found by summing the integrals over all the atomic orbitals (or corresponding unit vector atomic displacements or rotations). The resultant characters will, in general, be reducible to a combination of the characters of the irreducible representations \(\chi_i(S)\). To decompose the characters \(\chi(S)\) of the reducible representation to a sum of characters \(\chi_i(S)\) of the irreducible representation
\[\chi(S) = \sum_in_i\chi_i(S),\]
it is necessary to determine how many times, \(n_i\), the \(i^{\rm th}\) irreducible representation occurs in the reducible representation. The expression for \(n_i\) is
\[n_i =\dfrac{1}{g}\sum_S\chi(S)\chi_i(S)\]
in which \(g\) is the order of the point group- the total number of symmetry operations in the group (e.g., \(g = 6\) for \(C_{3v}\)).
For example, the reducible representation \(\chi(E) = 3, \chi(C_3) = 0\), and \(\chi(\sigma_v) = 1\) formed by the three \(1s_H\) orbitals discussed above can be decomposed as follows:
\[n_{A_1} = \dfrac{1}{6} (3 · 1 + 2 ·0 · 1 = 3 · 1 · 1 ) = 1,\]
\[n_{A_2} = \dfrac{1}{6} (3 · 1 + 2 ·0 · 1 = 3 · 1 · -1 ) = 0,\]
\[n_E = \dfrac{1}{6} (3 · 2 + 2 ·0 · -1 = 3 · 1 · 0 ) = 1.\]
These equations state that the three \(1s_H\) orbitals can be combined to give one \(A_1\) orbital and, since \(E\) is degenerate, one pair of \(E\) orbitals, as established above. With knowledge of the \(n_i\), the symmetry-adapted orbitals can be formed by allowing the projectors
\[P_i =\sum_i\chi_i(S)S\]
to operate on each of the primitive atomic orbitals. How this is carried out was illustrated for the \(1s_H\) orbitals in our earlier discussion. These tools allow a symmetry decomposition of any set of atomic orbitals into appropriate symmetry-adapted orbitals.
Before considering other concepts and group-theoretical machinery, it should once again be stressed that these same tools can be used in symmetry analysis of the translational, vibrational and rotational motions of a molecule. The twelve motions of \(NH_3\) (three translations, three rotations, six vibrations) can be described in terms of combinations of displacements of each of the four atoms in each of three \((x,y,z)\) directions. Hence, unit vectors placed on each atom directed in the \(x\), \(y\), and \(z\) directions form a basis for action by the operations {\(S\)} of the point group. In the case of \(NH_3\), the characters of the resultant 12 x 12 representation matrices form a reducible representation in the \(C_{2v}\) point group: \(\chi(E) = 12, \chi(C_3) = \chi(C_3^2) = 0\), \(\chi(\sigma_v) = \chi(\sigma_{v'}) = \chi(\sigma_{v"}) = 2\). For example under \(\sigma_v\), the \(H_2\) and \(H_3\) atoms are interchanged, so unit vectors on either one will not contribute to the trace. Unit z-vectors on \(N\) and \(H_1\) remain unchanged as well as the corresponding y-vectors. However, the x-vectors on \(N\) and \(H_1\) are reversed in sign. The total character for \(\sigma_{v'}\) the \(H_2\) and \(H_3\) atoms are interchanged, so unit vectors on either one will not contribute to the trace. Unit z-vectors on \(N\) and \(H_1\) remain unchanged as well as the corresponding y-vectors. However, the x-vectors on \(N\) and \(H_1\) are reversed in sign. The total character for \(\sigma_v\) is thus \(4 - 2 = 2\). This representation can be decomposed as follows:
\[n_{A_1} = \dfrac{1}{6} (1· 1· 12 + 2 ·1 ·0 + 3 · 1 · 2 ) = 3,\]
\[n_{A_2} = \dfrac{1}{6} (1· 1· 12 + 2 ·1 ·0 + 3 · -1 · 2 ) = 1,\]
\[ n_E = \dfrac{1}{6} (1· 2· 12 + 2 ·-1 ·0 + 3 · 0 · 2 ) = 4.\]
From the information on the right side of the \(C_{3v}\) character table, translations of all four atoms in the \(z\), \(x\) and \(y\) directions transform as \(A_1(z)\) and \(E(x,y)\), respectively, whereas rotations about the \(z(R_z)\), \(x(R_x)\), and \(y(R_y)\) axes transform as \(A_2\) and E. Hence, of the twelve motions, three translations have \(A_1\) and \(E\) symmetry and three rotations have \(A_2\) and \(E\) symmetry. This leaves six vibrations, of which two have \(A_1\) symmetry, none have \(A_2\) symmetry, and two (pairs) have \(E\) symmetry. We could obtain symmetry-adapted vibrational and rotational bases by allowing symmetry projection operators of the irreducible representation symmetries to operate on various elementary Cartesian \((x,y,z)\) atomic displacement vectors centered on the four atoms.
Direct Product Representations
Direct Products in N-Electron Wave functions
We now turn to the symmetry analysis of orbital products. Such knowledge is important because one is routinely faced with constructing symmetry-adapted \(N\)-electron configurations that consist of products of \(N\) individual spin orbitals, one for each electron. A point-group symmetry operator S, when acting on such a product of orbitals, gives the product of \(S\) acting on each of the individual orbitals
\[S(\phi_1\phi_2\phi_3...\phi_N) = (S\phi_1) (S\phi_2) (S\phi_3) ... (S\phi_N). \]
For example, reflection of an \(N\)-orbital product through the \(\sigma_v\) plane in \(NH_3\) applies the reflection operation to all \(N\) electrons.
Just as the individual orbitals formed a basis for action of the point-group operators, the configurations (\(N\)-orbital products) form a basis for the action of these same point-group operators. Hence, the various electronic configurations can be treated as functions on which \(S\) operates, and the machinery illustrated earlier for decomposing orbital symmetry can then be used to carry out a symmetry analysis of configurations.
Another shortcut makes this task easier. Since the symmetry adapted individual orbitals {\(\phi_i, i = 1, ..., M\)} transform according to irreducible representations, the representation matrices for the \(N\)-term products shown above consist of products of the matrices belonging to each \(\phi_i\). This matrix product is not a simple product but what is called a direct product. To compute the characters of the direct product matrices, one multiplies the characters of the individual matrices of the irreducible representations of the \(N\) orbitals that appear in the electron configuration. The direct-product representation formed by the orbital products can therefore be symmetry-analyzed (reduced) using the same tools as we used earlier.
For example, if one is interested in knowing the symmetry of an orbital product of the form \(a_1^2a_2^2e^2\) (note: lower case letters are used to denote the symmetry of electronic orbitals, whereas capital letters are reserved to label the overall configuration’s symmetry) in \(C_{3v}\) symmetry, the following procedure is used. For each of the six symmetry operations in the \(C_{2v}\) point group, the product of the characters associated with each of the six spin orbitals (orbital multiplied by á or â spin) is formed
\[\chi(S) = \prod_j\chi_j(S)= (\chi_{A_1}(S))^2 (\chi_{A_2}(S))^2 (\chi_E(S))^2.\]
In the specific case considered here, \(\chi (E) = 4\), \(\chi (2C_3) = 1\), and \(\chi (3\sigma_v) = 0\). Notice that the contributions of any doubly occupied non-degenerate orbitals (e.g., \(a_1^2\), and \(a_2^2\)) to these direct product characters \(\chi(S)\) are unity because for all operators \((\chi_k(S))^2 = 1\) for any one-dimensional irreducible representation. As a result, only the singly occupied or degenerate orbitals need to be considered when forming the characters of the reducible direct-product representation \(\chi(S)\). For this example this means that the direct-product characters can be determined from the characters \(\chi_E(S)\) of the two active (i.e., non-closed-shell) orbitals - the \(e^2\) orbitals. That is, \(\chi(S) = \chi_E(S)⋅\chi_E(S)\).
From the direct-product characters \(\chi(S)\) belonging to a particular electronic configuration (e.g., \(a_1^2a_2^2e^2\)), one must still decompose this list of characters into a sum of irreducible characters. For the example at hand, the direct-product characters \(\chi(S)\) decompose into one \(A_1\), one \(A_2\), and one \(E\) representation. This means that the \(e^2\) configuration contains \(A_1\), \(A_2\), and \(E\) symmetry elements. Projection operators analogous to those introduced earlier for orbitals can be used to form symmetry-adapted orbital products from the individual basis orbital products of the form \(a_1^2a_2^2e_x^me_y^{m'}\), where \(m\) and \(m'\) denote the occupation (1 or 0) of the two degenerate orbitals \(e_x\) and \(e_y\). In Appendix III of Electronic Spectra and Electronic Structure of Polyatomic Molecules , G. Herzberg, Van Nostrand Reinhold Co., New York, N.Y. (1966) the resolution of direct products among various representations within many point groups are tabulated.
When dealing with indistinguishable particles such as electrons, it is also necessary to further project the resulting orbital products to make them antisymmetric (for Fermions) or symmetric (for Bosons) with respect to interchange of any pair of particles. This step reduces the set of \(N\)-electron states that can arise. For example, in the above \(e^2\) configuration case, only \(^3A_2\), \(^1A_1\), and \(^1E\) states arise; the \(^3E\), \(^3A_1\), and \(^1A_2\) possibilities disappear when the antisymmetry projector is applied. In contrast, for an \(e^1e'^1\) configuration, all states arise even after the wave function has been made antisymmetric. The steps involved in combining the point group symmetry with permutational antisymmetry are illustrated in Chapter 6 of this text as well as in Chapter 10 of my QMIC text.
Direct Products in Selection Rules
Two states \(\psi_a\) and \(\psi_b\) that are eigenfunctions of a Hamiltonian \(H_o\) in the absence of some external perturbation (e.g., electromagnetic field or static electric field or potential due to surrounding ligands) can be "coupled" by the perturbation \(V\) only if the symmetries of \(V\) and of the two wave functions obey a so-called selection rule. In particular, only if the coupling integral
\[\int \psi_a^*V\psi_bd\tau= V_{a,b}\]
is non-vanishing will the two states be coupled by \(V\).
The role of symmetry in determining whether such integrals are non-zero can be demonstrated by noting that the integrand, considered as a whole, must contain a component that is invariant under all of the group operations (i.e., belongs to the totally symmetric representation of the group) if the integral is to not vanish. In terms of the projectors introduced above we must have
\[\sum_S\chi_A(S)S[\psi_a^*S\psi_b]\]
not vanish. Here the subscript \(A\) denotes the totally symmetric representation of whatever point group applies. The symmetry of the product \(\psi_a^*V\psi_b\) is, according to what was covered earlier, given by the direct product of the symmetries of \(\psi_a^*\) of \(V\) and of \(\psi_b\). So, the conclusion is that the integral will vanish unless this triple direct product contains, when it is reduced to its irreducible components, a component of the totally symmetric representation.
Another way to state the above result, and a way this is more often used in practice, is that the integral \(\int \psi_a V \psi_b \tau\) will vanish unless the symmetry of the direct product \(V\psi_b\) matches the symmetry of \(\psi_a^*\). Only when these symmetries match will the triple direct product contain a non-zero component of the totally symmetric representation. This is very much the same as what we saw earlier in this Chapter when we discussed how angular momentum coupling could limit which states contribute to the second-order perturbation theory energy. The angular momenta of \(V\) and of \(\psi_b\), when coupled, must have a component that matches the angular momentum of \(\psi_a\).
To see how this result is used, consider the integral that arises in formulating the interaction of electromagnetic radiation with a molecule within the electric-dipole approximation:
\[\int \psi_a^* \textbf{r} \psi_b d\tau\]
Here, \(\textbf{r}\) is the vector giving, together with \(e\), the unit charge, the quantum mechanical dipole moment operator
\[\textbf{r} = e\sum_nZ_n\textbf{R}_n - e\sum_i \textbf{r}_i,\]
where \(Z_n\) and \(\textbf{R}_n\) are the charge and position of the nth nucleus and \(\textbf{r}_j\) is the position of the jth electron. Now, consider evaluating this integral for the singlet \(n\rightarrow \pi^*\) transition in formaldehyde. Here, the closed-shell ground state is of \(^1A_1\) symmetry and the singlet excited state, which involves promoting an electron from the non-bonding \(b_2\) lone pair orbital on the Oxygen atom into the anti-bonding \(\pi^*\) \(b_1\) orbital on the CO moiety, is of \(^1A_2\) symmetry (\(b_1 \times b_2 = a_2\)). The direct product of the two wave function symmetries thus contains only \(a_2\) symmetry. The three components (\(x\), \(y\), and \(z\)) of the dipole operator have, respectively, \(b_1\), \(b_2\), and \(a_1\) symmetry. Thus, the triple direct products give rise to the following possibilities:
\[a_2 \times b_1 = b_2\]
\[a_2 \times b_2 = b_1\]
\[a_2 \times a_1 = a_2\]
There is no component of \(A_1\) symmetry in the triple direct product, so the integral vanishes. The alternative way of reaching this same conclusion is to notice that the direct product of the symmetries of the \(\pi^*\) \(b_1\) orbital and the \(b_2\) lone pair orbital is \(a_2 (b_1 \times b_2 = a_2\)), which does not match the symmetry of any component of the dipole operator. Either route allows us to conclude that the \(n\rightarrow \pi^*\) excitation in formaldehyde is electric dipole forbidden.
Overview
We have shown how to make a symmetry decomposition of a basis of atomic orbitals (or Cartesian displacements or orbital products) into irreducible representation components. This tool is very helpful when studying spectroscopy and when constructing the orbital correlation diagrams that form the basis of the Woodward-Hoffmann rules that play useful roles in predicting whether chemical reactions will have energy barriers in excess of thermodynamic barriers. We also learned how to form the direct-product symmetries that arise when considering configurations consisting of products of symmetry-adapted spin orbitals. Finally, we learned how the direct product analysis allows one to determine whether or not integrals of products of wave functions with operators between them vanish. This tool is of utmost importance in determining selection rules in spectroscopy and for determining the effects of external perturbations on the states of the species under investigation.
Contributors and Attributions
Jack Simons (Henry Eyring Scientist and Professor of Chemistry, U. Utah) Telluride Schools on Theoretical Chemistry
Integrated by Tomoyuki Hayashi (UC Davis)


