3.2: Normal Modes of Vibration
- Page ID
- 11577
Having seen how one can use information about the gradients and Hessians on a Born-Oppenheimer surface to locate geometries corresponding to stable species and transition states, let us now move on to see how this same data is used to treat vibrations on this surface.
For a polyatomic molecule whose electronic energy's dependence on the \(3N\) Cartesian coordinates of its \(N\) atoms, the potential energy \(V\) can be expressed (approximately) in terms of a Taylor series expansion about any of the local minima. Of course, different local minima (i.e., different isomers) will have different values for the equilibrium coordinates and for the derivatives of the energy with respect to these coordinates. The Taylor series expansion of the electronic energy is written as:
\[V (g_k) = V(0) + \sum_k \left(\dfrac{\partial V}{\partial q_k}\right) q_k + \dfrac{1}{2} \sum_{j,k} q_j H_{j,k} q_k \, + \, ... \]
Here,
- \(V(0)\) is the energy at the current geometry,
- \(\dfrac{\partial{V}}{\partial{q_k}} = g_k\) is the gradient of the energy along the \(q_k\) coordinate,
- \(H_{j,k} = \dfrac{\partial^2{V}}{\partial{q_j}\partial{q_k}}\) is the second-derivative or Hessian matrix, and
- \(g_k\) is the length of the “step” to be taken along this Cartesian direction.
If the geometry corresponds to a minimum or transition state, the gradient terms will all vanish, and the Hessian matrix will possess \(3N - 5\) (for linear species) or \(3N -6\) (for non-linear molecules) positive eigenvalues and 5 or 6 zero eigenvalues (corresponding to 3 translational and 2 or 3 rotational motions of the molecule) for a minimum and one negative eigenvalues and \(3N-6\) or \(3N-7\) positive eigenvalues for a transition state.
The Newton Equations of Motion for Vibration
The Kinetic and Potential Energy Matrices
Truncating the Taylor series at the quadratic terms (assuming these terms dominate because only small displacements from the equilibrium geometry are of interest), one has the so-called harmonic potential:
\[V(q_k) = V(0) + \dfrac{1}{2} \sum_{j,k} q_j H_{j,k} q_k \label{3.2.1} \]
The classical mechanical equations of motion for the \(3N \{q_k\}\) coordinates can be written in terms of the above potential energy and the following kinetic energy function:
\[T = \dfrac{1}{2} \sum_j m_j \left(\dfrac{dq_j}{dt}\right)^2, \label{3.2.2}\]
where \(\dfrac{dq_j}{dt}\) is the time rate of change of the coordinate \(q_j\) and \(m_j\) is the mass of the atom on which the \(j^{th}\) Cartesian coordinate resides. The Newton equations thus obtained are:
\[m_j\dfrac{d^2 q_j}{dt^2}=-\sum_k H_{j,k}q_k \]
where the force along the \(j^{th}\) coordinate is given by minus the derivative of the potential \(V\) along this coordinate
\[\dfrac{\partial{V}}{\partial{q_j}}= \sum_k H_{j,k} q_k \label{3.2.3}\]
within the harmonic approximation. These classical equations can more compactly be expressed in terms of the time evolution of a set of so-called mass-weighted Cartesian coordinates defined as:
\[x_j = q_j \sqrt{(m_j)} \label{3.2.4}\]
in terms of which the above Newton equations become
\[\dfrac{d^2 x_j}{dt^2}=-\sum_k H'_{j,k}x_k\]
and the mass-weighted Hessian matrix elements are
\[ H'_{j,k} = \dfrac{H_{j,k}}{ \sqrt{m_jm_k} }. \label{3.2.5}\]
The Harmonic Vibrational Energies and Normal Mode Eigenvectors
Assuming that the \(x_j\) undergo some form of sinusoidal time evolution:
\[x_j(t) = x_j (0) \cos(\omega t),\]
and substituting this into the Newton equations produces a matrix eigenvalue equation:
\[\omega^2 x_j = \sum_k H'_{j,k} x_k \]
in which the eigenvalues are the squares of the so-called normal mode vibrational frequencies and the eigenvectors give the amplitudes of motion along each of the \(3N\) mass-weighted Cartesian coordinates that belong to each mode. Hence, to perform a normal-mode analysis of a molecule, one forms the mass-weighted Hessian matrix and then finds the \(3N-5\) or \(3N-6\) non-zero eigenvalues \(\omega_j^2\) as well as the corresponding eigenvectors \(x_k^{(j)}\).
It is useful to note that, if this same kind of analysis were performed at a geometry corresponding to a transition state, \(3N-6\) or \(3N-7\) of the \(\omega_j^2\) values would be positive, but one of them would be negative. The eigenvector corresponding to the negative eigenvalue of the mass-weighted Hessian points along a very important direction that we will discuss later; it is the direction of the so-called intrinsic reaction coordinate (IRC). When reporting the eigenvalues \(\omega_j^2\) at such a transition-state geometry, one often says that there is one imaginary frequency because one of the \(\omega_j^2\) values is negative; this value of \(\omega_j^2\) characterizes the curvature of the energy surface along the IRC at the transition state. The positive vibrational eigenvalues of transition-state geometries are used, as discussed in Chapter 8, to evaluate statistical mechanics partition functions for reaction rates, and the negative \(\omega_j^2\) value plays a role in determining the extent of tunneling through the barrier on the reaction surface.
Within this harmonic treatment of vibrational motion, the total vibrational energy of the molecule is given as
\[E(\nu_1, \nu_2, ··· \nu_{3N-5\text{ or }6}) =\sum_{j=1}^{3N-5\text{ or }6}\hbar\omega_j\Big(\nu_j+\dfrac{1}{2}\Big) \]
a sum of \(3N-5\) or \(3N-6\) independent contributions one for each normal mode. The corresponding total vibrational wave function
\[\Psi = \prod_{j=1}^{3N-5\text{ or }6} \psi\nu_j (x^{(j)}) \]
is a product of \(3N-5\) or \(3N-6\) harmonic oscillator functions \(\psi\nu_j (x^{(j)})\) one for each normal mode. The energy gap between one vibrational level and another in which one of the \( \nu_j\) quantum numbers is increased by unity (i.e., for fundamental vibrational transitions) is
\[\Delta E_{\nu_j} \rightarrow \nu_j + 1 = \hbar \omega_j \]
The harmonic model thus predicts that the "fundamental" (\(\nu=0 \rightarrow \nu = 1\)) and "hot band" (\(\nu=1 \rightarrow \nu = 2\)) transitions should occur at the same energy, and the overtone (\(\nu=0 \rightarrow \nu=2\)) transitions should occur at exactly twice this energy.
One might wonder whether mass-weighted Cartesian coordinates would be better or more appropriate to use when locating minima and transition states on Born-Oppenheimer energy surfaces. Although mass-weighted coordinates are indeed essential for evaluating harmonic vibrational frequencies and, as we will see later, for tracing out so-called intrinsic reaction paths, their use produces the same minima and transition states as one finds using coordinates that are mass-weighted. This is because the condition that all components of the gradient
\[\dfrac{\partial V}{\partial q_j}=0\]
of the energy surface vanish at a minimum or at a transition state will automatically be obeyed when expressed in terms of mass-weighted coordinates since
\[\dfrac{\partial V}{\partial q_j}=\dfrac{\partial V}{\partial x_j}\dfrac{\partial x_j}{\partial q_j}=\dfrac{\partial V}{\partial x_j}\sqrt{m_j}\]
Notice that this means the geometries of all local minima and transition states on a given Born-Oppenheimer surface will be exactly the same regardless of what isotopes appear in the molecule. For example, for the reactions
\[ H-CN \rightarrow H-NC \]
or
\[D-CN \rightarrow D-NC \]
\[ H_2C=O \rightarrow H_2 + CO\]
or
\[HDC=O \rightarrow HD + CO\]
or
\[D_2C=O \rightarrow D_2 + CO \]
the geometries of the reactants, products, and transition states (for each of the distinct reactions) will not depend on the identity of the hydrogen isotopes. However, the harmonic vibrational frequencies will depend on the isotopes because the mass-weighted Hessian differs from the Hessian expressed in terms of non-mass-weighted coordinates.
The Use of Symmetry
Symmetry Adapted Modes
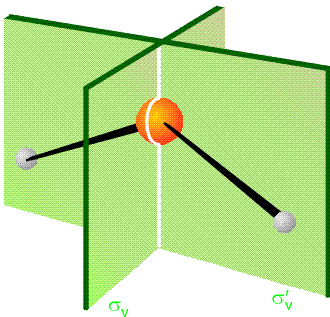
It is often possible to simplify the calculation of the normal mode harmonic frequencies and eigenvectors by exploiting molecular point group symmetry. For molecules that possess symmetry at a particular stable geometry, the electronic potential \(V(q_j)\) displays symmetry with respect to displacements of symmetry equivalent Cartesian coordinates. For example, consider the water molecule at its \(C_{2v}\) equilibrium geometry as illustrated in Figure 3.2. A very small movement of the \(H_2O\) molecule's left \(H\) atom in the positive \(x\) direction (\(\Delta x_L\)) produces the same change in the potential \(V\) as a correspondingly small displacement of the right \(H\) atom in the negative \(x\) direction
(\(-\Delta x_R\)). Similarly, movement of the left H in the positive y direction (\(\Delta y_L\)) produces an energy change identical to movement of the right H in the positive y direction (\(\Delta y_R\)).
The equivalence of the pairs of Cartesian coordinate displacements is a result of the fact that the displacement vectors are connected by the point group operations of the \(C_{2v}\) group. In particular, reflection of \(\Delta x_L\) through the yz plane (the two planes are depicted in Figure 3.3) produces \(-\Delta x_R\), and reflection of \(\Delta y_L\) through this same plane yields \(\Delta y_R\).
More generally, it is possible to combine sets of Cartesian displacement coordinates {\(q_k\)} into so-called symmetry adapted coordinates {\(Q_{\Gamma_j}\)}, where the index \(\Gamma\) labels the irreducible representation in the appropriate point group and j labels the particular combination of that symmetry (i.e., there may be more than one kind of displacement that has a given symmetry G). These symmetry-adapted coordinates can be formed by applying the point group projection operators (that are treated in detail in Chapter 4) to the individual Cartesian displacement coordinates.
To illustrate, again consider the \(H_2O\) molecule in the coordinate system described above. The \(3N = 9\) mass-weighted Cartesian displacement coordinates (\(X_L, Y_L, Z_L, X_O, Y_O, Z_O, X_R, Y_R, Z_R\)) can be symmetry adapted by applying the following four projection operators:
\[P_{A_1} = 1 + \sigma_{yz} + \sigma_{xy} + C_2 \]
\[P_{b_1} = 1 + \sigma_{yz} - \sigma_{xy} - C_2 \]
\[P_{b_2} = 1 - \sigma_{yz} + \sigma_{xy} - C_2 \]
\[P_{a_2} = 1 - \sigma_{yz} - \sigma_{xy} + C_2 \]
to each of the 9 original coordinates (the symbol s denotes reflection through a plane and \(C_2\) means rotation about the molecule’s \(C_2\) axis). Of course, one will not obtain 9 x 4 = 36 independent symmetry adapted coordinates in this manner; many identical combinations will arise, and only 9 will be independent.
The independent combinations of \(a_1\) symmetry (normalized to produce vectors of unit length) are
\[Q_{a_1,1} = \dfrac{1}{\sqrt{2}} [X_L- X_R]\]
\[Q_{a_1,2} = \dfrac{1}{\sqrt{2}} [Y_L + Y_R]\]
\[Q_{a_1,3} = [Y_O]\]
Those of \(b_2\) symmetry are
\[Q_{b_2,1} = \dfrac{1}{\sqrt{2}} [X_L+ X_R]\]
\[Q_{b_2,2} = \dfrac{1}{\sqrt{2}} [Y_L - Y_R]\]
\[Q_{b_2,3} = [X_O],\]
and the combinations
\[Q_{b_1,1} = \dfrac{1}{\sqrt{2}} [Z_L + Z_R]\]
\[Q_{b_1,2} = [Z_O]\]
are of \(b_1\) symmetry, whereas
\[Q_{a_2,1} = \dfrac{1}{\sqrt{2}} [Z_L - Z_R]\]
is of \(a_2\) symmetry.
Point Group Symmetry of the Harmonic Potential
These nine symmetry-adapted coordinates \(Q_{\Gamma_j}\) are expressed as unitary transformations of the original mass-weighted Cartesian coordinates:
\[Q_{\Gamma_j} = C_{\Gamma_{j,k}} X_k \]
These transformation coefficients \({C_{\Gamma_{j,k}}}\) can be used to carry out a unitary transformation of the 9x9 mass-weighted Hessian matrix. In so doing, we need only form blocks
\[H_{\Gamma_{j,l}} = \sum_{k,k’} C_{\Gamma_{j,k}} H_{k,k'} \sqrt{m_k m_{k'}} C_{\Gamma_{l,k'}} \]
within which the symmetries of the two modes are identical. The off-diagonal elements
\[H_{\Gamma_j\Gamma'_l}= \sum_{k,k’} C_{\Gamma_{j,k}} H_{k,k'} \sqrt{m_k m_{k'}} C_{\Gamma'_{l,k'}} \]
vanish because the potential \(V(q_j)\) (and the full vibrational Hamiltonian \(H = T + V\)) commutes with the \(C_{2V}\) point group symmetry operations.
As a result, the 9x9 mass-weighted Hessian eigenvalue problem can be subdivided into two 3x3 matrix problems (of \(a_1\) and \(b_2\) symmetry), one 2x2 matrix of \(b_1\) symmetry and one 1x1 matrix of \(a_2\) symmetry. For example, the \(a_1\) symmetry block His formed as follows:
\[
\left[\begin{array}{ccc}
\dfrac{1}{\sqrt{2}} & -\dfrac{1}{\sqrt{2}} & 0 \\
\dfrac{1}{\sqrt{2}} & \dfrac{1}{\sqrt{2}} & 0 \\
0 & 0 & 1
\end{array}\right]
\left[\begin{array}{ccc}
m_H^{-1/2}\dfrac{\partial^2 V}{\partial x_L^2}m_H^{-1/2} & m_H^{-1/2}\dfrac{\partial^2 V}{\partial x_L \partial x_R}m_H^{-1/2} & m_H^{-1/2}\dfrac{\partial^2 V}{\partial x_L \partial y_O}m_H^{-1/2}\\
m_H^{-1/2}\dfrac{\partial^2 V}{\partial x_R \partial x_L}m_H^{-1/2} & m_H^{-1/2}\dfrac{\partial^2 V}{\partial x_R^2}m_H^{-1/2} & m_H^{-1/2}\dfrac{\partial^2 V}{\partial x_R \partial y_O}m_H^{-1/2}\\
m_H^{-1/2}\dfrac{\partial^2 V}{\partial y_O \partial x_L}m_H^{-1/2} & m_H^{-1/2}\dfrac{\partial^2 V}{\partial y_O \partial x_R}m_H^{-1/2} & m_H^{-1/2}\dfrac{\partial^2 V}{\partial y_O^2}m_H^{-1/2}
\end{array}\right]
\left[\begin{array}{ccc}
\dfrac{1}{\sqrt{2}} & \dfrac{1}{\sqrt{2}} & 0 \\
-\dfrac{1}{\sqrt{2}} & \dfrac{1}{\sqrt{2}} & 0 \\
0 & 0 & 1
\end{array}\right]
\]
The \(b_2\), \(b_1\) and \(a_2\) blocks are formed in a similar manner. The eigenvalues of each of these blocks provide the squares of the harmonic vibrational frequencies, the eigenvectors provide the coefficients \(\{C_{\Gamma_{j,k}}\}\) of the \(j^{\rm th}\) normal mode of symmetry \(\Gamma\) in terms of the mass-weighted Cartesian coordinates {\(X_k\)}. The relationship \(X_k = q_k \sqrt{(m_k)}\) can then be used to express these coefficients in terms of the original Cartesian coordinates {\(q_k\)}.
Regardless of whether symmetry is used to block diagonalize the mass-weighted Hessian, six (for non-linear molecules) or five (for linear species) of the eigenvalues will equal zero. The eigenvectors belonging to these zero eigenvalues describe the 3 translations and 2 or 3 rotations of the molecule. For example, when expressed in terms of the original (i.e., non-mass-weighted) Cartesian coordinates
\[\dfrac{1}{\sqrt{3}}[x_L + x_R + x_O]\]
\[\dfrac{1}{\sqrt{3}}[y_L + y_R + y_O]\]
\[\dfrac{1}{\sqrt{3}}[z_L +z_R + z_O]\]
are three translation eigenvectors of \(b_2\), \(a_1\) and \(b_1\) symmetry, and
\[\dfrac{1}{\sqrt{2}}(z_L-z_R)\]
is a rotation (about the y-axis in the Figure 3.2) of \(a_2\) symmetry. This rotation vector can be generated by applying the \(a_2\) projection operator to \(z_L\) or to \(z_R\). The other two rotations are of \(b_1\) and \(b_2\) symmetry and involve spinning of the molecule about the \(x\)- and \(z\)- axes of the Figure 3.2, respectively.
So, of the 9 Cartesian displacements, 3 are of \(a_1\) symmetry, 3 of \(b_2\), 2 of \(b_1\), and 1 of \(a_2\). Of these, there are three translations (\(a_1\), \(b_2\), and \(b_1\)) and three rotations (\(b_2\), \(b_1\), and a2). This leaves two vibrations of \(a_1\) and one of \(b_2\) symmetry. For the \(H_2O\) example treated here, the three non-zero eigenvalues of the mass-weighted Hessian are therefore of \(a_1\), \(b_2\), and \(a_1\) symmetry. They describe the symmetric and asymmetric stretch vibrations and the bending mode, respectively as illustrated in Figure 3.4.
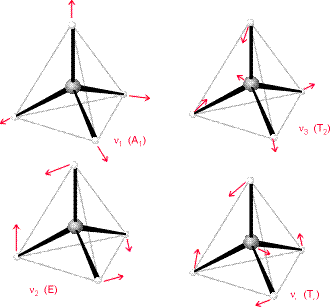
The method of vibrational analysis presented here can work for any polyatomic molecule. One knows the mass-weighted Hessian and then computes the non-zero eigenvalues, which then provide the squares of the normal modes’ harmonic vibrational frequencies. Point group symmetry can be used to block diagonalize this Hessian and to label the vibrational modes according to symmetry as we show in Figure 3.5 for the \(CF_4\) molecule in tetrahedral symmetry.
Contributors and Attributions
Jack Simons (Henry Eyring Scientist and Professor of Chemistry, U. Utah) Telluride Schools on Theoretical Chemistry
Integrated by Tomoyuki Hayashi (UC Davis)


