8.2: Conformational Analysis

Last updated
Save as PDF

Page ID: 215733

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Conformational analysis is the study of the different energy levels associated with the different conformations of a molecule. Conformations are the different 3-dimensional arrangements that the molecule can acquire by freely rotating around σ-bonds. One must keep in mind that conformations are not isomers. Isomers are different molecules. Conformations are simply different structural arrangements of the same molecule. The example below illustrates four out of an infinite number of conformations that the n-butane molecule can acquire by freely rotating around the C₂-C₃ bond, indicated in yellow. The red arrow indicates the direction of the rotation. The methyl carbons (C₁ and C₄) are indicated in red and all the hydrogen atoms in white. In this example C₁, C₂ and C₃ remain stationary while C₄ gradually moves down from top right to bottom right.

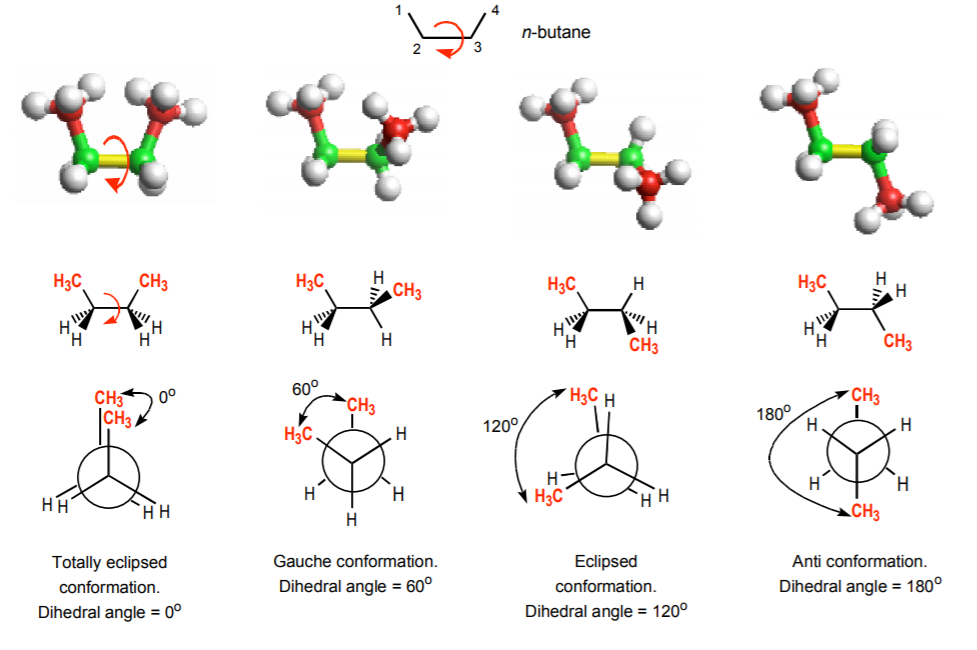
NEWMAN PROJECTIONS AND DIHEDRAL (TORSIONAL) ANGLE

The type of drawing used at the bottom of the figure in the last page is called a Newman projection, or representation. It is widely used to represent the conformations of open-chain alkanes that result as rotation around a sigma bond occurs. Another way to visualize Newman projections is to imagine them as the shadow a molecule would cast against a wall if a light beam was directed along the carbon-carbon axis under consideration.

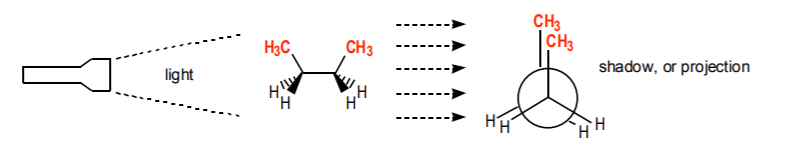
A concept strongly associated with Newman projections is dihedral angle. It is defined as the angle between any two atoms attached to neighboring carbons in the Newman projection. For example, the two methyl groups above (in red) are attached to neighboring carbons. The angle between the two as seen in the Newman projection is zero (that is, they overlap, or” eclipse” each other). This is then the dihedral angle between those methyl groups.

CONFORMATIONAL ENERGY

The relationship between molecular structure and potential energy is a major area of study in organic chemistry. It has applications in conformational analysis because we are interested in relating the structure of conformers to their energy, and therefore to their relative stabilities. Remember that the relationship between potential energy and stability is inverse. The higher the potential energy of a system the lower its stability. Also remember that these are always relative concepts. There is no absolute energy or stability. They are always measured relative to a previously agreed upon standard.

There are three factors that increase the potential energy of conformers and therefore decrease their stability. They are:

a) Steric interactions - Crowding of alkyl groups or other substituents as they come too close together.

b) Torsional strain - Tendency of s-bonds to rotate in order to acquire a more stable conformation.

c) Angle strain - Increase in potential energy due to bond angles being forced to depart from ideal values in cycloalkanes and other rings.

STERIC INTERACTIONS

The term steric interactions refers to interference that occurs between atoms or groups of atoms by virtue of their size, or volume. When bulky groups or large molecules get too close to each other, steric interactions can become severe, raising the potential energy of the system. When these groups are allowed to drift far apart, steric interactions are relieved and the system gains stability.

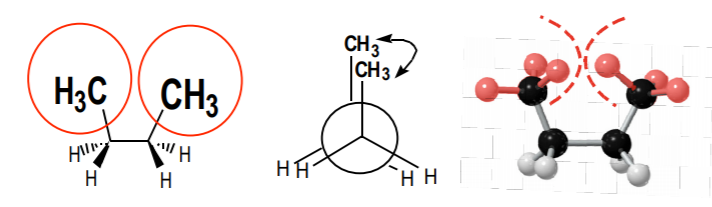
Three representations of steric interactions, or “crowding,” between the two methyl groups in the eclipsed conformation of n-butane.

TORSIONAL STRAIN

This term is closely related to dihedral angle (also called torsional angle). Free rotation around sigma bonds changes the dihedral angle and therefore can bring bulky groups together or apart. When the dihedral angle is small and bulky groups interact (such as in the illustration above), there is a driving force for the molecule to rotate around the C₂-C₃ axis to relieve the steric interactions between the methyl groups. If this drive is impeded and the molecule is forced to acquire the eclipsed conformation, or a small dihedral angles between bulky groups, then torsional strain results. This might be the case for example in cyclic systems, where free rotation around sigma bonds is limited or impeded. Obviously, torsional strain increases the energy of a system and therefore decreases its stability.

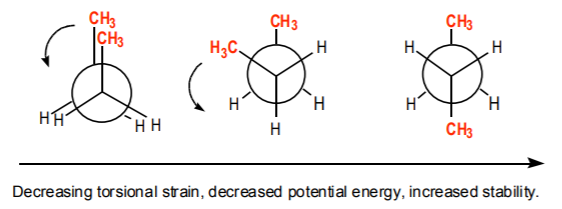
As the molecule rotates around the C₂-C₃ bond, steric crowding between the methyl groups gets relieved.