6.5: Orbital Picture of Delocalization
- Page ID
- 215700
The orbital view of delocalization can get somewhat complicated. For now we’re going to keep it at a basic level. We start by noting that sp2 carbons actually come in several varieties. Two of the most important and common are neutral sp2 carbons and positively charged sp2 carbons. Substances containing neutral sp2 carbons are regular alkenes. Species containing positively charged sp2 carbons are called carbocations. The central carbon in a carbocation has trigonal planar geometry, and the unhybridized p orbital is empty. The following representations convey these concepts.
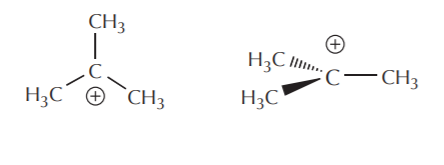
Top and side view of a carbocation in Lewis and 3-D notation
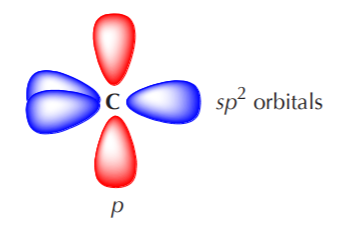
Orbital view of a carbocation. The unhybridized p orbital is empty
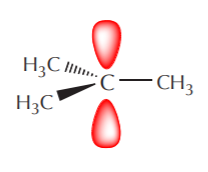
A combination of orbital and Lewis or 3-D formulas is a popular means of representing certain features that we may want to highlight. For example, if we’re not interested in the sp2 orbitals and we just want to focus on what the p orbitals are doing we can use the following notation.
Let’s now focus on two simple systems where we know delocalization of pi electrons exists. One is a system containing two pi bonds in conjugation, and the other has a pi bond next to a positively charged carbon. We can represent these systems as follows.

Line angle and orbital picture of a simple conjugated system
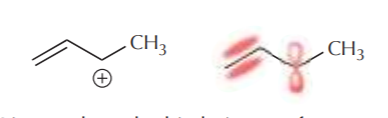
Line angle and orbital picture of a system containing a carbocation next to a pi bond
If we focus on the orbital pictures, we can immediately see the potential for electron delocalization. The two pi molecular orbitals shown in red on the left below are close enough to overlap. Overlapping is a good thing because it delocalizes the electrons and spreads them over a larger area, bringing added stability to the system.

It is however time-consuming to draw orbitals all the time. The following representations are used to represent the delocalized system.
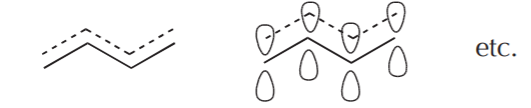
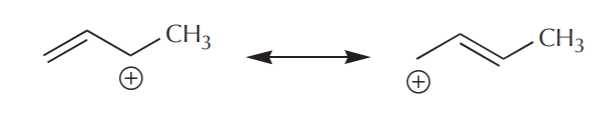
A similar process applied to the carbocation leads to a similar picture.

The resonance representation conveys the idea of delocalization of charge and electrons rather well.
Finally, the following representations are sometimes used, but again, the simpler they are, the less accurately they represent the delocalization picture.

There will be plenty of opportunity to observe more complex situations as the course progresses.


