5.4: Hybridization of Carbon

Last updated
Save as PDF

Page ID: 215679

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

ALKENES AND sp² HYBRIDIZATION OF CARBON

We will now reproduce the sp³hybridization process for carbon, but instead of taking one s and three p orbitals to make four equivalent sp³ orbitals, this time we’ll take only one s and two p orbitals to make three equivalent sp² orbitals, leaving one p orbital untouched. The process is shown below.

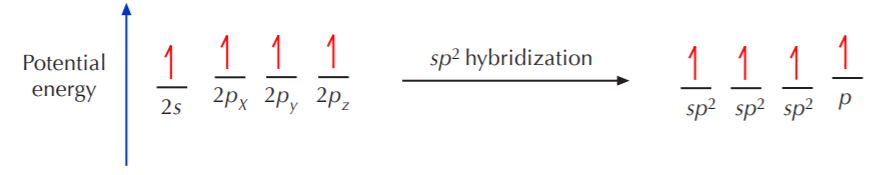
As shown, the three resulting sp² orbitals are equivalent in energy, but the remaining p orbital has not been affected. It still retains its original energy and shape. Again, according to VSEPR theory, equivalent orbitals will arrange themselves in 3-D space to be as far apart from each other as possible. Therefore, the three equivalent sp² orbitals will arrange themselves in a trigonal planar configuration. That is to say, the carbon nucleus will be at the center of an equilateral triangle, and the three sp² orbitals will point to the corners of that triangle. The ideal angle between sp² orbitals is therefore 120^o. A top view of this arrangement is shown below.

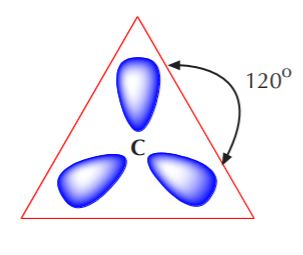
In this top view, the unhybridized p orbital cannot be seen because it also arranges itself to be as far apart from the sp² orbitals as possible. That is to say, it is positioned at right angles to those orbitals, with one lobe coming out of the plane of the page and the other going behind the page. To see this arrangement clearly, we must switch to a side view of the orbital system.

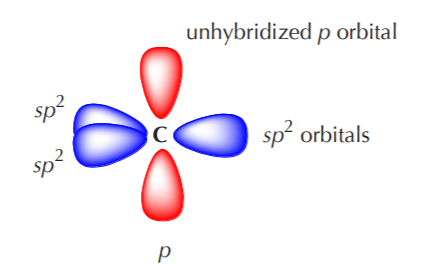
When two sp² hybridized carbon atoms approach each other to bond, two sp²orbitals approach each other head to head, and two p orbitals approach each other sideways. The bond formed by the sp² orbitals is a sigma bond, and the bond formed by the p orbitals is called a pi bond. The process is shown below.

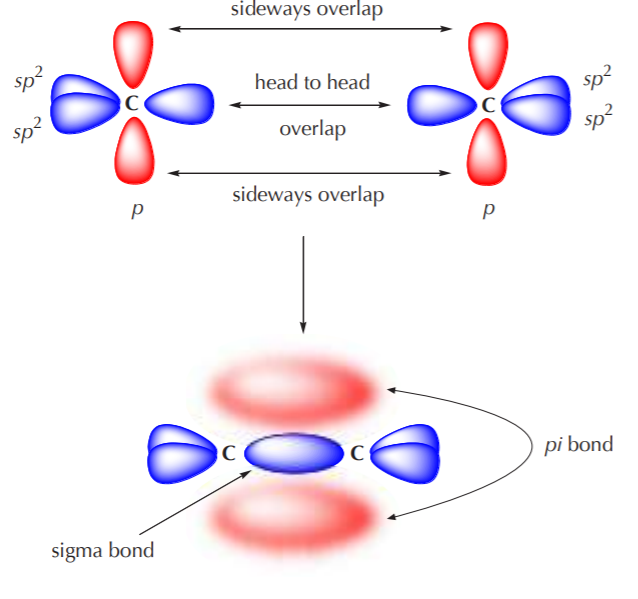
The illustration above tries to convey a basic feature of the pi bond as compared to the sigma bond. The sigma bond is short and strong. As a rule, head to head overlap is the most efficient way to bond and results in relatively strong and stable bonds. The pi bond, on the other hand, is relatively long and diffuse. Sideways overlap is less efficient than head to head overlap and results in formation of weaker bonds.

This has some implications in the properties and chemical reactivity of sigma and pi bonds. The electrons in the sigma bond (or sigma electrons) are more tightly bound to the nucleus and don’t move too much. In other words, they are more LOCALIZED. The electrons in the pi bond (or pi electrons) are less tightly bound by the nucleus, and therefore they are relatively mobile. Under certain conditions, they have the capability to become DELOCALIZED, that is to say, they can move in the molecular skeleton from one atom to another, or even become spread over several atoms, according to principles we’ll study later.

At the same time, in chemical reactions where electrons are to be traded, the pi electrons are more readily available because they are more exposed and less tightly bound by the nucleus. It is relatively easy to break a pi bond compared to the sigma bond. The principles of all this chemistry will be discussed later in the course.

ALKENES ARE HYDROCARBONS THAT CONTAIN AT LEAST ONE PI BOND AS PART OF THEIR MOLECULAR STRUCTURE. By this definition, the simplest possible alkene must contain two carbon atoms. It is called ethene. Below is a Lewis and a line-angle representation of ethene, which is sometimes informally called ethylene. Notice that although C–H bonds are not usually shown in line-angle formulas, sometimes they are included for enhanced clarity. In this case a pure line-angle formula for ethene would look awkward because it would resemble an equal sign (=).

Notice that a Lewis representation does not differentiate between the sigma and the pi bonds in the so-called “double bond.” It simply shows the two together as two equal dashes. The orbital picture better represents the actual nature of the two types of bonds. Additional examples are shown below. For a full discussion of the structure of alkenes refer to chapter 7 of the Wade textbook.

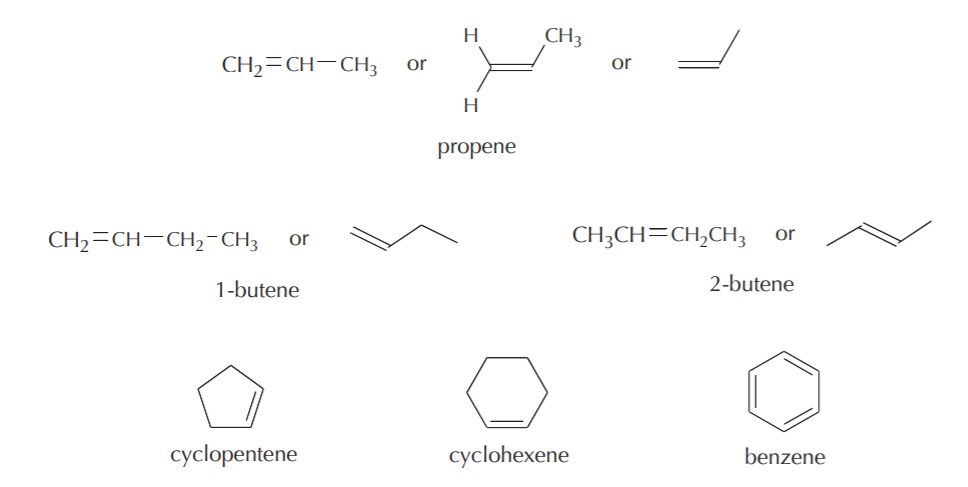
Observe that the general formula for open chain monoalkenes –that is, alkenes that do not form cyclic structures and which contain only one pi bond– is C_nH_2n where n is the total number of carbon atoms.

ALKYNES AND sp HYBRIDIZATION OF CARBON

The process for understanding the sp hybridization process for carbon is basically an extension of the other two types (sp³ and sp²). You should try to work out this scheme on your own and see if your predictions agree with those presented in the textbook. sp hybridization gives rise to the formation of hydrocarbons known as alkynes. Alkynes contain at least one triple bond, and have linear geometry around the carbons comprising the triple bond. Therefore, the ideal angle between the sp hybrid orbitals is 180^o. Some examples of alkynes are shown below. For additional information refer to chapter 9 of the Wade textbook.

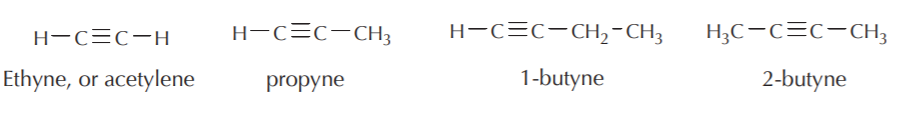
Observe that the general formula for open chain monoalkynes is C_nH_2n-2 where n is the total number of carbon atoms.