5.2: Orbital Hybridization Theory

Last updated
Save as PDF

Page ID: 215674

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

If we look at the valence shell configuration of carbon, we find two paired electrons in the 2s orbital, and two unpaired electrons in the 2p_X and 2p_Y orbitals, one in each:

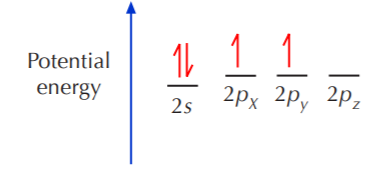
In order to fulfill the octet rule, carbon must use its 4 valence electrons when bonding to other atoms. However, only unpaired electrons can bond. That means that the two paired electrons occupying the 2s orbital must become unpaired before they can bond. Since the energy gap between the 2s and 2p orbitals is very small, one of the 2s electrons can be promoted to the empty 2p orbital, leading to the following situation

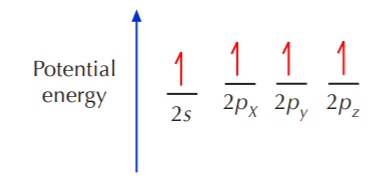
Now the four electrons appear to be ready for bonding, but there is a problem. The 2p orbitals are known to be at right angles to each other. If bonding occurs in this state, the 3 equivalent p electrons would form 3 equivalent bonds oriented at 90^o to each other, and the s electron would form a bond of a different type and orientation from the other three. No such compound exists. The simplest hydrocarbon –methane (CH₄)– is known to have tetrahedral geometry, where the four C–H bonds are all equivalent and positioned at 109.5^o angles to each other. In addition, there are some carbon compounds where the bond angles are 120^o or even 180^o. The shapes and relative positions of the valence orbitals in atomic carbon do not explain the shapes and relative positions of the bonds in carbon compounds.

HYBRIDIZATION THEORY ATTEMPTS TO EXPLAIN THE ACTUAL SHAPES OF MOLECULES BY INVOKING THE FORMATION OF HYBRID ORBITALS DURING, OR PRIOR TO, THE BONDING PROCESS.

Going back to the carbon model with four unpaired electrons in the valence shell, we can take it as a point of departure for formation of hybrid orbitals. The first step is to take either 2, 3, or all four of those orbitals and equalize their energies. Let’s say that we take all four of them and form 4 equivalent new orbitals. These orbitals are now of the same energy, which is intermediate between those of the original 2s and 2p orbitals. At the same time, we cannot name the new orbitals s or p, for they’re neither. We have to find a new name that reflects the fact that they were created from one s orbital and three p orbitals. We will call them sp³orbitals. The process that leads to their formation is called sp³ hybridization.

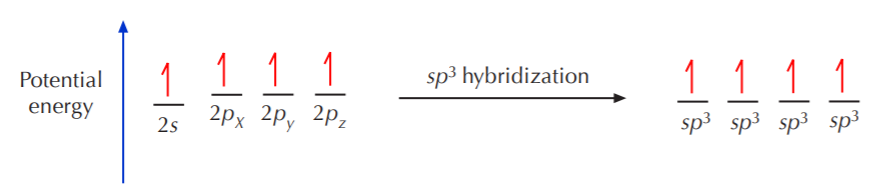
All four sp³ orbitals that result from this process are equivalent. That means that they have the same size, shape, and energy. According to VSEPR (valence shell electron pair repulsion) theory, such orbitals will orient themselves in 3-D space to be as far apart from each other as possible. The resulting shape is then a tetrahedron, where the carbon nucleus is at the center and the orbitals point to the corners of the tetrahedron. The ideal angle between orbitals is then 109.5 degrees.

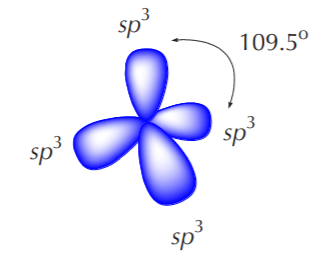
When an sp³ hybridized carbon bonds to hydrogen, it forms methane, whose geometry is known to be tetrahedral.

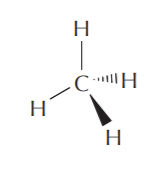
A 3-D representation of methane. The single lines represent bonds that are positioned on the plane of the paper. The solid wedge represents a bond coming out of the plane of the paper towards the front. The broken wedge represents a bond going behind the plane of the paper towards the back.

HYDROCARBONS

Hydrocarbons are substances containing only carbon and hydrogen. Hydrocarbons are classified into the following major categories: alkanes, alkenes, alkynes, and aromatic hydrocarbons. In the following pages we will do an overview of the basic characteristics of the first three, but will postpone the study of aromatics until later.

ALKANES AND sp³ HYBRIDIZATION OF CARBON

Alkanes are hydrocarbons where all the carbon atoms are sp³-hybridized, all bonds are single bonds, and all carbons are tetrahedral. Methane is the simplest alkane, followed by ethane, propane, butane, etc. The carbon chain constitutes the basic skeleton of alkanes. Carbon chains with four or more atoms can be linear or branched. Some examples are shown below including Lewis, molecular, and condensed formulas. Refer to chapter 2 of the Wade textbook for additional examples.

Linear alkanes

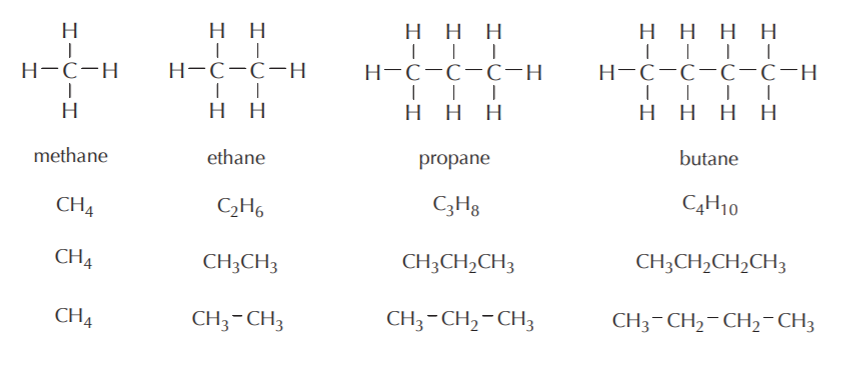
Some examples of branched alkanes are shown below. Notice that sometimes Lewis formulas become cumbersome and difficult to write without cluttering. Condensed formulas are more convenient to use in such situations.

Branched alkanes

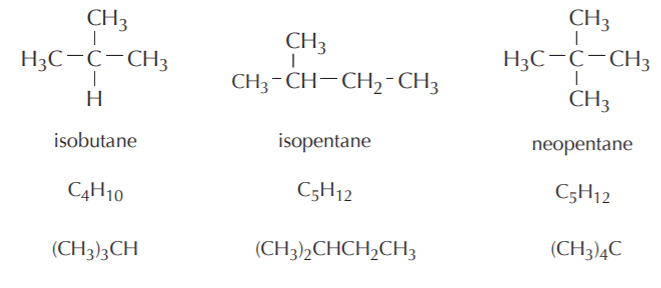
As can be seen from the above examples, all alkanes have the general formula C_nH_2n₊₂ where n is the total number of carbon atoms. This holds regardless of whether the alkane is linear or branched.