4.3: Resonance Structures

RESONANCE STRUCTURES AND SOME LIMITATIONS OF LEWIS FORMULAS:

Lewis formulas are misleading in the sense that atoms and electrons are shown as being static. By being essentially two-dimensional representations they also fail to give an accurate idea of the three-dimensional features of the molecule, such as actual bond angles and topography of the molecular frame.

Furthermore, a given compound can have several valid Lewis formulas. For example CH₃CNO can be represented by at least three different but valid Lewis structures called resonance forms, or resonance structures, shown below.

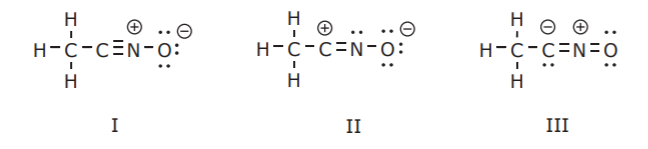
However, a stable compound such as the above does not exist in multiple states represented by structures I, or II, or III. The compound exists in a single state called a hybrid of all three structures. That is, it contains contributions of all three resonance forms, much like a person might have physical features inherited from each parent to varying degrees.

In the resonance forms shown above the atoms remain in one place. The basic bonding pattern, or connectivity, is the same in all structures, but some electrons have changed locations. This means that there are certain rules for electron mobility that enable us to “push” electrons around to arrive from one resonance structure to another. These rules will be examined in detail in a later paper.

ALL RESONANCE STRUCTURES MUST BE VALID LEWIS FORMULAS:

By convention, we use double-headed arrows to indicate that several resonance structures contribute to the same hybrid. Continuing with the example we’ve been using, the resonance structures for CH₃CNO should be written in this way if we want to emphasize that they represent the same hybrid.

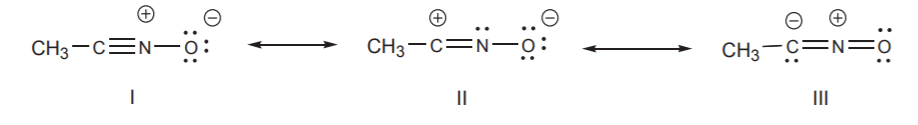
Do not confuse double-headed arrows with double arrows. A double arrow indicates that two or more species are in equilibrium with each other and therefore have a separate existence. Double-headed arrows indicate resonance structures that do not exist by themselves. They simply represent features that the actual molecule, the hybrid, possesses to one extent or another.

When writing resonance structures keep in mind that THEY ALL MUST BE VALID LEWIS FORMULAS. The factors that make up valid Lewis formulas are as follows.

1. Observe the rules of covalent bonding, including common patterns as discussed previously. Make sure to show all single, double, and triple bonds.

2. Account for the total number of valence electrons being shared (from all the elements), including bonding and nonbonding electrons. Make sure to show these nonbonding electrons.

3. Account for the net charge of the molecule or species, showing formal charges where they belong.

4. Observe the octet rule as much as possible, but also understand that there are instances where some atoms may not fulfill this rule.

5. Avoid having unpaired electrons (single electrons with no partners) unless the total number of valence electrons for all elements is an odd number. This is not a very frequent occurrence, but the following example shows a species that could exist as a reaction intermediate in some high energy environments.

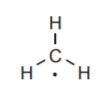
The total number of valence electrons being shared for all atoms is 4 from carbon and 3 from the three hydrogens, for a total of 7. Because it is an odd number, it is impossible to have all these electrons paired. Therefore the presence of a single electron cannot be avoided. Notice that there is no formal charge on carbon, since it has no surplus or deficit of valence electrons.

RELATIVE ENERGIES OF RESONANCE STRUCTURES.

From the examples given so far it can be seen that some resonance forms are structurally equivalent and others are not. The potential energy associated with equivalent Lewis structures is the same. If the Lewis structures are not equivalent, then the potential energy associated with them is most likely different. This means that equivalent resonance structures are also equivalent in stability and nonequivalent structures have different stabilities. This in turn means that equivalent structures contribute equally to the hybrid and nonequivalent structures do not contribute equally to the hybrid.

In the example below, the two structures are equivalent. Therefore they make equal contributions to the hybrid.

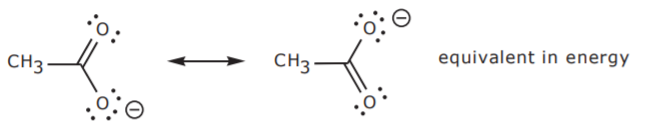
It is very difficult to accurately represent the hybrid with drawings because it is a composite of all the resonance contributors. Some representations such as the first one shown below are sometimes given. In this case the broken line represents the electrons and the negative charge which are spread over three atoms (O-C-O). Another commonly used representation of the hybrid is given on the right, showing that each oxygen atom shares a -1/2 charge. However, none of them accurately conveys the true picture. For convenience, the unshared electrons are sometimes omitted from some representations, just like it’s done with hydrogen atoms. This must be kept in mind when examining the different structures.

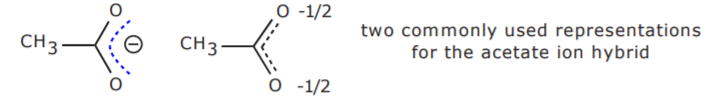
There is a third resonance form that can be drawn for the acetate ion hybrid. The structure shown below is structurally different from the ones shown above. This means that it is of different energy and therefore does not contribute to the hybrid to the same extent as the others. In this case, it happens to be less stable than the other two and therefore does not make a significant contribution to the hybrid.

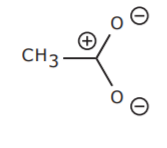
What factors dictate the relative stabilities of different resonance structures? Charge separation is an important one. In the example just given there are too many charges present in the structure (even though the net charge is still the same). This results in a structure with higher potential energy than others with fewer or no formal charges. This structure is less stable and its contribution to the hybrid is probably minor.

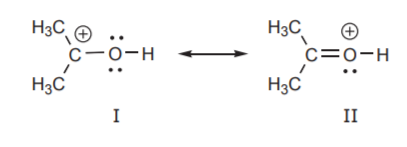
Another important factor that increases potential energy (lowers stability) is the presence of atoms with an incomplete octet. In the example below structure I has a carbon atom with a positive charge and therefore an incomplete octet. Based on this criterion, this structure is less stable than structure II and makes a less significant contribution to the hybrid.

Finally, another factor that comes into play when determining the relative energies of resonance structures is the relative electronegativities of atoms that bear charges. More electronegative atoms are more comfortable with negative charges. Less electronegative atoms are more comfortable with positive charges. In the example below, structure I is less stable than II. The negative charge is on carbon, which is less electronegative than oxygen. Therefore structure II makes a larger contribution to the hybrid.

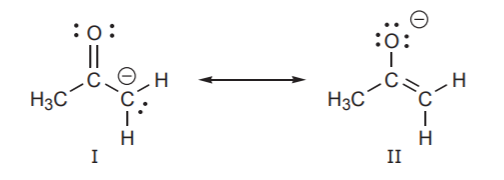
Some texts refer to the different contributors as “important” or “unimportant.” This can be misleading, because “importance” is context-dependent. In the example above, structure I is less important in terms of its contribution to the hybrid, but in terms of reactivity, it is very important. It will be seen later that this structure provides a better indication of how this species reacts with electrophiles in certain types of reactions.

Based on the charge separation criterion, structure II below might be labeled “unimportant,” or “less important” because it is less stable than I. But if we are trying to assess the polarity of this molecule, structure II becomes very important because it reveals that the carbon atom has positive character and the oxygen has negative character. The hybrid representation on the right then portrays the molecule as a polar molecule, which structure I alone does not give much indication of.

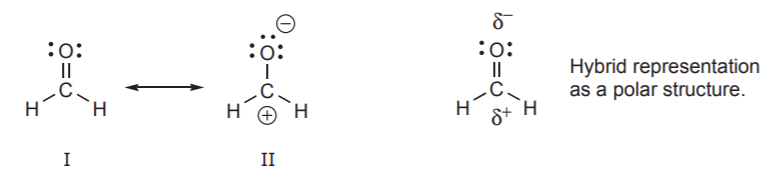
The following additional examples further illustrate the relative importance of the factors that contribute to structural energy and stability.