2.3: Resonance
- Page ID
- 31386
After completing this section, you should be able to
- draw resonance forms for molecules and ions.
Make certain that you can define, and use in context, the key term below.
- resonance form
- delocalization
Resonance Delocalization
Sometimes, even when formal charges are considered, the bonding in some molecules or ions cannot be described by a single Lewis structure. Resonance is a way of describing delocalized electrons within certain molecules or polyatomic ions where the bonding cannot be expressed by a single Lewis formula. A molecule or ion with such delocalized electrons is represented by several contributing structures (also called resonance contributors or canonical forms). Resonance contributors involve the ‘imaginary movement’ of pi-bonded electrons or of lone-pair electrons that are adjacent to pi bonds. Note, sigma bonds cannot be broken during resonance – if you show a sigma bond forming or breaking, you are showing a chemical reaction taking place. Likewise, the positions of atoms in the molecule cannot change between resonance contributors.
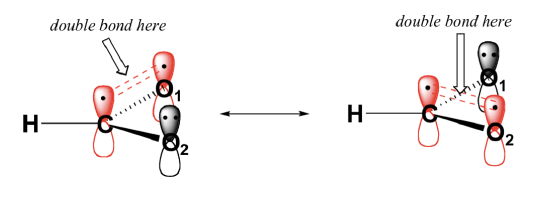
When looking at the structure of the molecule, formate, we see that there are two equivalent structures possible. Which one is correct? There are two simple answers to this question: 'both' and 'neither one'. Both ways of drawing the molecule are equally acceptable approximations of the bonding picture for the molecule, but neither one, by itself, is an accurate picture of the delocalized pi bonds. The two alternative drawings, however, when considered together, give a much more accurate picture than either one on its own. This is because they imply, together, that the carbon-carbon bonds are not double bonds, not single bonds, but about halfway in between.
Formate Ion Structures are Equivalent in Energy
When it is possible to draw more than one valid structure for a compound or ion, we have identified resonance contributors: two or more different Lewis structures depicting the same molecule or ion that, when considered together, do a better job of approximating delocalized pi-bonding than any single structure. By convention, resonance contributors are linked by a double-headed arrow, and are sometimes enclosed by brackets:
The depiction of formate using the two resonance contributors A and B in the figure above does not imply that the molecule at one moment looks like structure A, then at the next moment shifts to look like structure B. Rather, at all moments, the molecule is a combination, or resonance hybrid of both A and B. Each individual resonance contributor of the formate ion is drawn with one carbon-oxygen double bond (120 pm) and one carbon-oxygen single bond (135 pm), with a negative formal charge located on the single-bonded oxygen. However, the two carbon-oxygen bonds in formate are actually the same length (127 pm) which implies that neither resonance contributor is correct. Although there is an overall negative formal charge on the formate ion, it is shared equally between the two oxygens. Therefore, the formate ion can be more accurately depicted by a pair of resonance contributors. Alternatively, a single structure can be used, with a dashed line depicting the resonance-delocalized pi bond and the negative charge located in between the two oxygens.
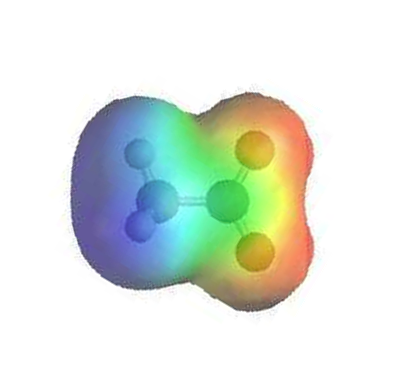
The electrostatic potential map of formate shows that there is an equal amount of electron density (shown in red) around each oxygen.
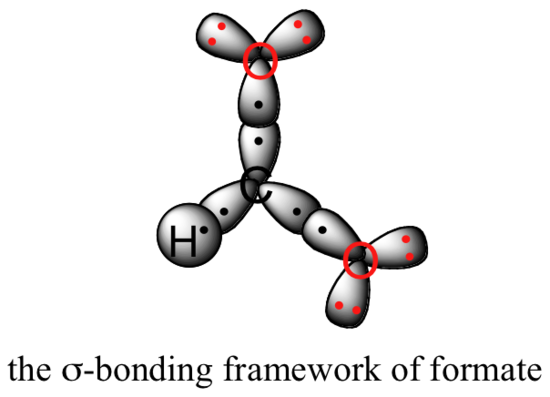
Valence bond theory can be used to develop a picture of the bonding in a carboxylate group. We know that the carbon must be sp2-hybridized, (the bond angles are close to 120˚, and the molecule is planar), and we will treat both oxygens as being sp2-hybridized as well. Both carbon-oxygen sigma bonds, then, are formed from the overlap of carbon sp2 orbitals and oxygen sp2 orbitals.
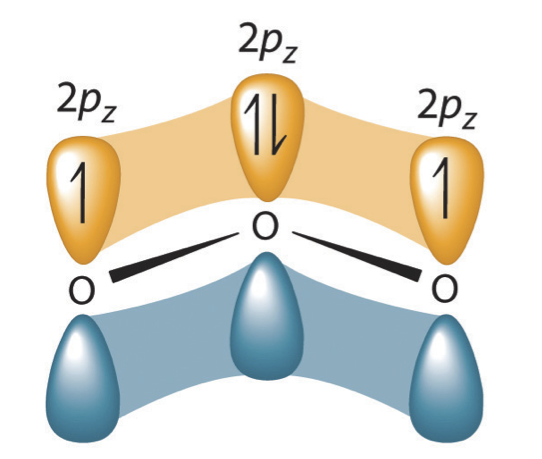
In addition, the carbon and both oxygens each have an un-hybridized 2pz orbital situated perpendicular to the plane of the sigma bonds. These three 2pz orbitals are parallel to each other, and can overlap in a side-by-side fashion to form a delocalized pi bond.
Overall, the situation is one of three parallel, overlapping 2pz orbitals sharing four delocalized pi electrons. Because there is one more electron than there are 2pz orbitals, the system has an overall charge of 1–. Resonance contributors are used to approximate overlapping 2pz orbitals and delocalized pi electrons. Molecules with resonance are usually drawn showing only one resonance contributor for the sake of simplicity. However, identifying molecules with resonance is an important skill in organic chemistry.
This example shows an important exception to the general rules for determining the hybridization of an atom. The oxygen with the negative charge appears to be sp3 hybridized because it is surrounded by four electron groups. However, this representation of the oxygen atom is not correct because it is actually part of a resonance hybrid. A pair of lone pair of electrons on the negatively charged oxygen are not localized in an sp3 orbital, rather, they are delocalized as part of a conjugated pi system. The stability gained though resonance is enough to cause the expected sp3 to become sp2. The sp2 hybridization gives the oxygen a p orbital allowing it to participate in conjugation. As a general rule sp3 hybridized atoms with lone pair electrons tend to become sp2 hybridized when adjacent to a conjugated system.
Example: Carbonate (CO32−)
Like formate, the electronic structure of the carbonate ion cannot be described by a single Lewis electron structure. Unlike O3, though, the Lewis structures describing CO32− has three equivalent representations.![]()
1. Because carbon is the least electronegative element, we place it in the central position:
2. Carbon has 4 valence electrons, each oxygen has 6 valence electrons, and there are 2 more for the 2− charge. This gives 4 + (3 × 6) + 2 = 24 valence electrons.
3. Six electrons are used to form three bonding pairs between the oxygen atoms and the carbon:
4. We divide the remaining 18 electrons equally among the three oxygen atoms by placing three lone pairs on each and indicating the 2− charge:
5. There are no electrons left for the central atom.![]()
6. At this point, the carbon atom has only 6 valence electrons, so we must take one lone pair from an oxygen and use it to form a carbon–oxygen double bond. In this case, however, there are three possible choices:
As with formate, none of these structures describes the bonding exactly. Each predicts one carbon–oxygen double bond and two carbon–oxygen single bonds, but experimentally all C–O bond lengths are identical. We can write resonance structures (in this case, three of them) for the carbonate ion:
As the case for formate, the actual structure involves the formation of a molecular orbital from pz orbitals centered on each atom and sitting above and below the plane of the CO32− ion. ![]()
Benzene is a common organic solvent that was previously used in gasoline; it is no longer used for this purpose, however, because it is now known to be a carcinogen. The benzene molecule (C6H6) consists of a regular hexagon of carbon atoms, each of which is also bonded to a hydrogen atom. Use resonance structures to describe the bonding in benzene. Given: molecular formula and molecular geometry Asked for: resonance structures Strategy: A Draw a structure for benzene illustrating the bonded atoms. Then calculate the number of valence electrons used in this drawing. B Subtract this number from the total number of valence electrons in benzene and then locate the remaining electrons such that each atom in the structure reaches an octet. C Draw the resonance structures for benzene. Solution: A Each hydrogen atom contributes 1 valence electron, and each carbon atom contributes 4 valence electrons, for a total of (6 × 1) + (6 × 4) = 30 valence electrons. If we place a single bonding electron pair between each pair of carbon atoms and between each carbon and a hydrogen atom, we obtain the following: Each carbon atom in this structure has only 6 electrons and has a formal charge of 1+, but we have used only 24 of the 30 valence electrons. B If the 6 remaining electrons are uniformly distributed pair-wise on alternate carbon atoms, we obtain the following: Three carbon atoms now have an octet configuration and a formal charge of 1−, while three carbon atoms have only 6 electrons and a formal charge of 1+. We can convert each lone pair to a bonding electron pair, which gives each atom an octet of electrons and a formal charge of 0, by making three C=C double bonds. C There are, however, two ways to do this: Each structure has alternating double and single bonds, but experimentation shows that each carbon–carbon bond in benzene is identical, with bond lengths (139.9 pm) intermediate between those typically found for a C–C single bond (154 pm) and a C=C double bond (134 pm). We can describe the bonding in benzene using the two resonance structures, but the actual electronic structure is an average of the two. The existence of multiple resonance structures for aromatic hydrocarbons like benzene is often indicated by drawing either a circle or dashed lines inside the hexagon: This combination of p orbitals for benzene can be visualized as a ring with a node in the plane of the carbon atoms. As can be seen in an electrostatic potential map of benzene, the electrons are distributed symmetrically around the ring. The sodium salt of nitrite is used to relieve muscle spasms. Draw two resonance structures for the nitrite ion (NO2−).

Exercises
Extra example - O3
A molecule or ion with such delocalized electrons is represented by several contributing structures (also called resonance structures or canonical forms). Such is the case for ozone (O3), an allotrope of oxygen with a V-shaped structure and an O–O–O angle of 117.5°.
1. We know that ozone has a V-shaped structure, so one O atom is central:
2. Each O atom has 6 valence electrons, for a total of 18 valence electrons.
3. Assigning one bonding pair of electrons to each oxygen–oxygen bond gives
4. If we place three lone pairs of electrons on each terminal oxygen, we obtain
and have 2 electrons left over.
5. At this point, both terminal oxygen atoms have octets of electrons. We therefore place the last 2 electrons on the central atom:
6. The central oxygen has only 6 electrons. We must convert one lone pair on a terminal oxygen atom to a bonding pair of electrons—but which one? Depending on which one we choose, we obtain either
Which is correct? In fact, neither is correct. Both predict one O–O single bond and one O=O double bond. If the bonds were of different types (one single and one double, for example), they would have different lengths. It turns out, however, that both O–O bond distances are identical, 127.2 pm, which is shorter than a typical O–O single bond (148 pm) and longer than the O=O double bond in O2 (120.7 pm).![]()
Equivalent Lewis dot structures, such as those of ozone, are called resonance structures . The position of the atoms is the same in the various resonance structures of a compound, but the position of the electrons is different. Double-headed arrows link the different resonance structures of a compound: