12.6: Infrared Spectroscopy
- Page ID
- 31527
After completing this section, you should be able to
- identify (by wavelength, wavenumber, or both) the region of the electromagnetic spectrum which is used in infrared (IR) spectroscopy.
- interconvert between wavelength and wavenumber.
- discuss, in general terms, the effect that the absorption of infrared radiation can have on a molecule.
Make certain that you can define, and use in context, the key terms below.
- infrared spectrum
- wavenumber (reciprocal centimetres)
Notice that the scale at the bottom of the infrared spectrum for 2-hexanone shown is calibrated in wavenumbers (cm−1). A wavenumber is the reciprocal of a wavelength (1/λ); thus, a wavenumber of 1600 cm−1 corresponds to a wavelength of
Organic chemists find it more convenient to deal with wavenumbers rather than wavelengths when discussing infrared spectra.
You will obtain infrared spectra for a number of the compounds you will synthesize in the laboratory component of this course.
The inverted peaks observed in the spectra correspond to molecular stretching and bending vibrations that only occur at certain quantized frequencies. When infrared radiation matching these frequencies falls on the molecule, the molecule absorbs energy and becomes excited. Eventually the molecule returns to its original (ground) state, and the energy which was absorbed is released as heat.
Infrared Spectroscopy
The full range of electromagnetic radiation wavelengths is referred to as the electromagnetic spectrum.
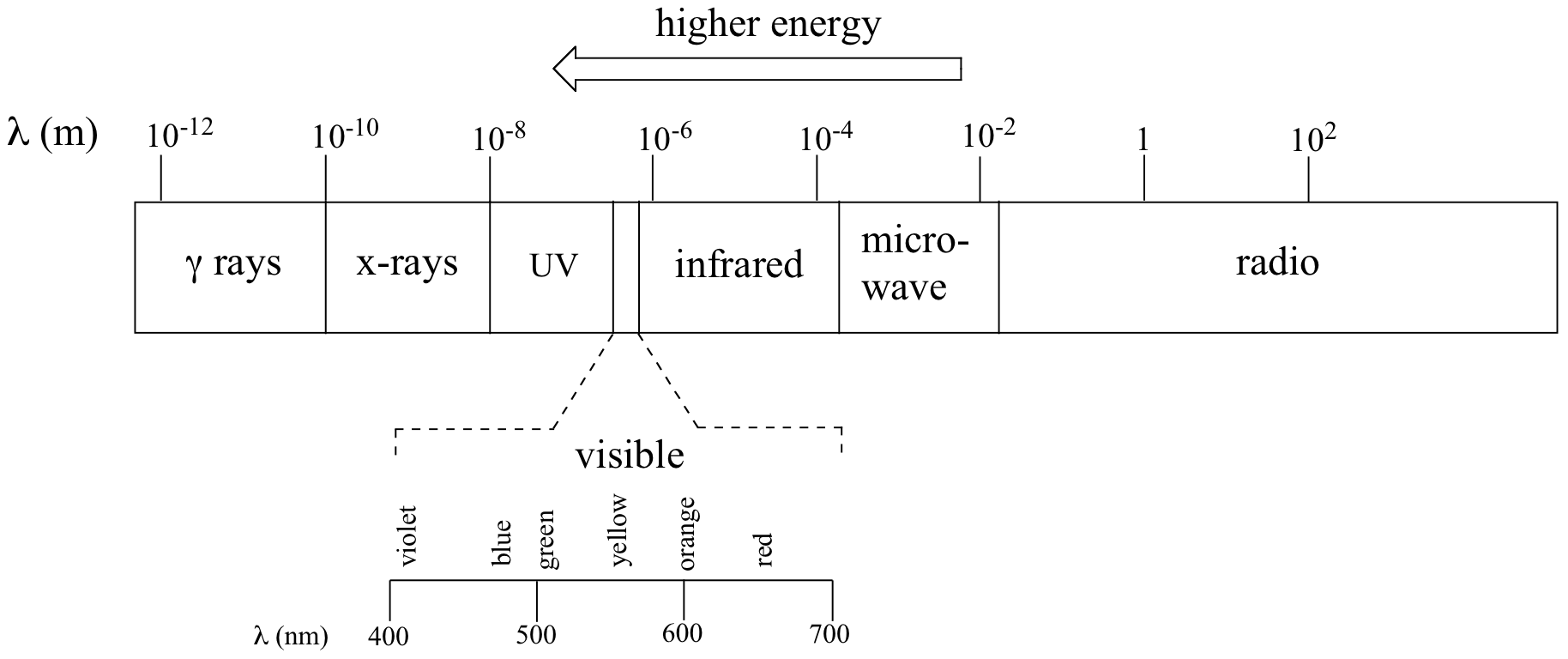
Notice in the figure above that infrared light is lower energy than visible light. The wavelengths of infrared radiation are between 0.8 and 250 μm. The units that are typically used for infrared spectroscopy are wavenumbers (which is cm-1). IR spectroscopy analyzes radiation between 40 to 13,000 cm-1. But what type of excitation is occurring when infrared radiation is absorbed by a molecule?
Covalent bonds in organic molecules are not rigid sticks – rather, they behave more like springs. At room temperature, organic molecules are always in motion, as their bonds stretch, bend, and twist. These complex vibrations can be broken down mathematically into individual vibrational modes, a few of which are illustrated below.
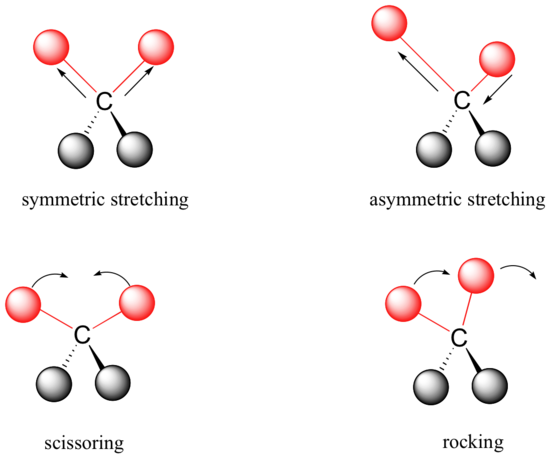
The energy of molecular vibration is quantized rather than continuous, meaning that a molecule can only stretch and bend at certain 'allowed' frequencies. If a molecule is exposed to electromagnetic radiation that matches the frequency of one of its vibrational modes, it will in most cases absorb energy from the radiation and jump to a higher vibrational energy state - what this means is that the amplitude of the vibration will increase, but the vibrational frequency will remain the same. The difference in energy between the two vibrational states is equal to the energy associated with the wavelength of radiation that was absorbed. It turns out that it is the infrared region of the electromagnetic spectrum which contains frequencies corresponding to the vibrational frequencies of organic bonds.
Let's take 2-hexanone as an example. Picture the carbonyl bond of the ketone group as a spring. This spring is constantly bouncing back and forth, stretching and compressing, pushing the carbon and oxygen atoms further apart and then pulling them together. This is the stretching mode of the carbonyl bond. In the space of one second, the spring 'bounces' back and forth 5.15 x 1013 times - in other words, the ground-state frequency of carbonyl stretching for a the ketone group is about 5.15 x 1013 Hz.
If our ketone sample is irradiated with infrared light, the carbonyl bond will specifically absorb light with this same frequency, which by equations 4.1 and 4.2 corresponds to a wavelength of 5.83 x 10-6 m and an energy of 4.91 kcal/mol. When the carbonyl bond absorbs this energy, it jumps up to an excited vibrational state.

The value of ΔE - the energy difference between the low energy (ground) and high energy (excited) vibrational states - is equal to 4.91 kcal/mol, the same as the energy associated with the absorbed light frequency. The molecule does not remain in its excited vibrational state for very long, but quickly releases energy to the surrounding environment in form of heat, and returns to the ground state.
With an instrument called an infrared spectrophotometer, we can 'see' this vibrational transition. In the spectrophotometer, infrared light with frequencies ranging from about 1013 to 1014 Hz is passed though our sample of cyclohexane. Most frequencies pass right through the sample and are recorded by a detector on the other side.
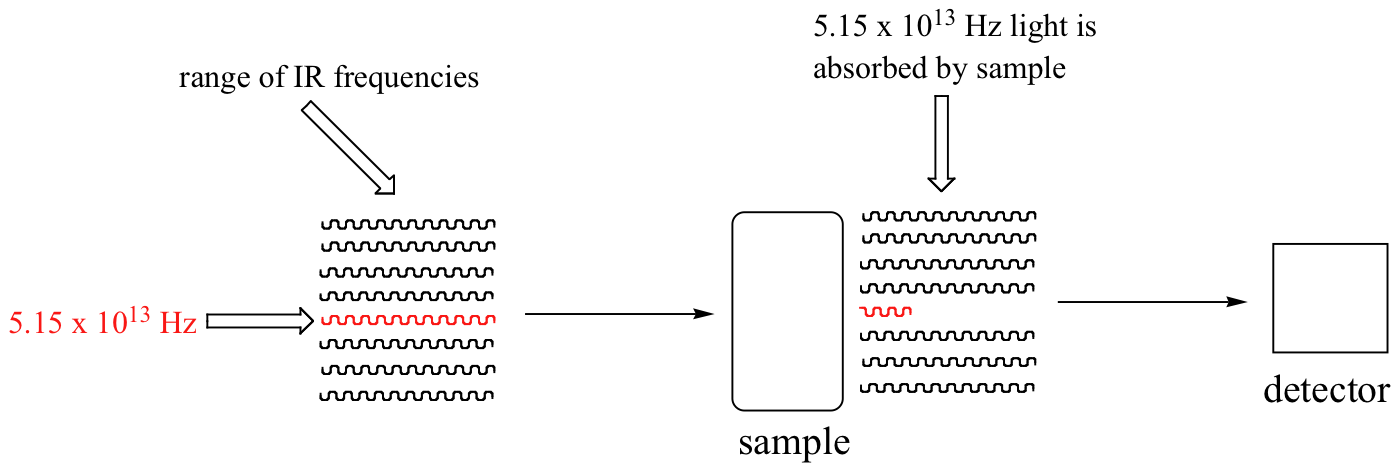
Our 5.15 x 1013 Hz carbonyl stretching frequency, however, is absorbed by the 2-hexanone sample, and so the detector records that the intensity of this frequency, after having passed through the sample, is something less than 100% of its initial intensity.
The vibrations of a 2-hexanone molecule are not, of course, limited to the simple stretching of the carbonyl bond. The various carbon-carbon bonds also stretch and bend, as do the carbon-hydrogen bonds, and all of these vibrational modes also absorb different frequencies of infrared light.
The power of infrared spectroscopy arises from the observation that different functional groups have different characteristic absorption frequencies. The carbonyl bond in a ketone, as we saw with our 2-hexanone example, typically absorbs in the range of 5.11 - 5.18 x 1013 Hz, depending on the molecule. The carbon-carbon triple bond of an alkyne, on the other hand, absorbs in the range 6.30 - 6.80 x 1013 Hz. The technique is therefore very useful as a means of identifying which functional groups are present in a molecule of interest. If we pass infrared light through an unknown sample and find that it absorbs in the carbonyl frequency range but not in the alkyne range, we can infer that the molecule contains a carbonyl group but not an alkyne.
Some bonds absorb infrared light more strongly than others, and some bonds do not absorb at all. In order for a vibrational mode to absorb infrared light, it must result in a periodic change in the dipole moment of the molecule. Such vibrations are said to be infrared active. In general, the greater the polarity of the bond, the stronger its IR absorption. The carbonyl bond is very polar, and absorbs very strongly. The carbon-carbon triple bond in most alkynes, in contrast, is much less polar, and thus a stretching vibration does not result in a large change in the overall dipole moment of the molecule. Alkyne groups absorb rather weakly compared to carbonyls.
Some kinds of vibrations are infrared inactive. The stretching vibrations of completely symmetrical double and triple bonds, for example, do not result in a change in dipole moment, and therefore do not result in any absorption of light (but other bonds and vibrational modes in these molecules do absorb IR light).

Now, let's look at some actual output from IR spectroscopy experiments. Below is the IR spectrum for 2-hexanone.
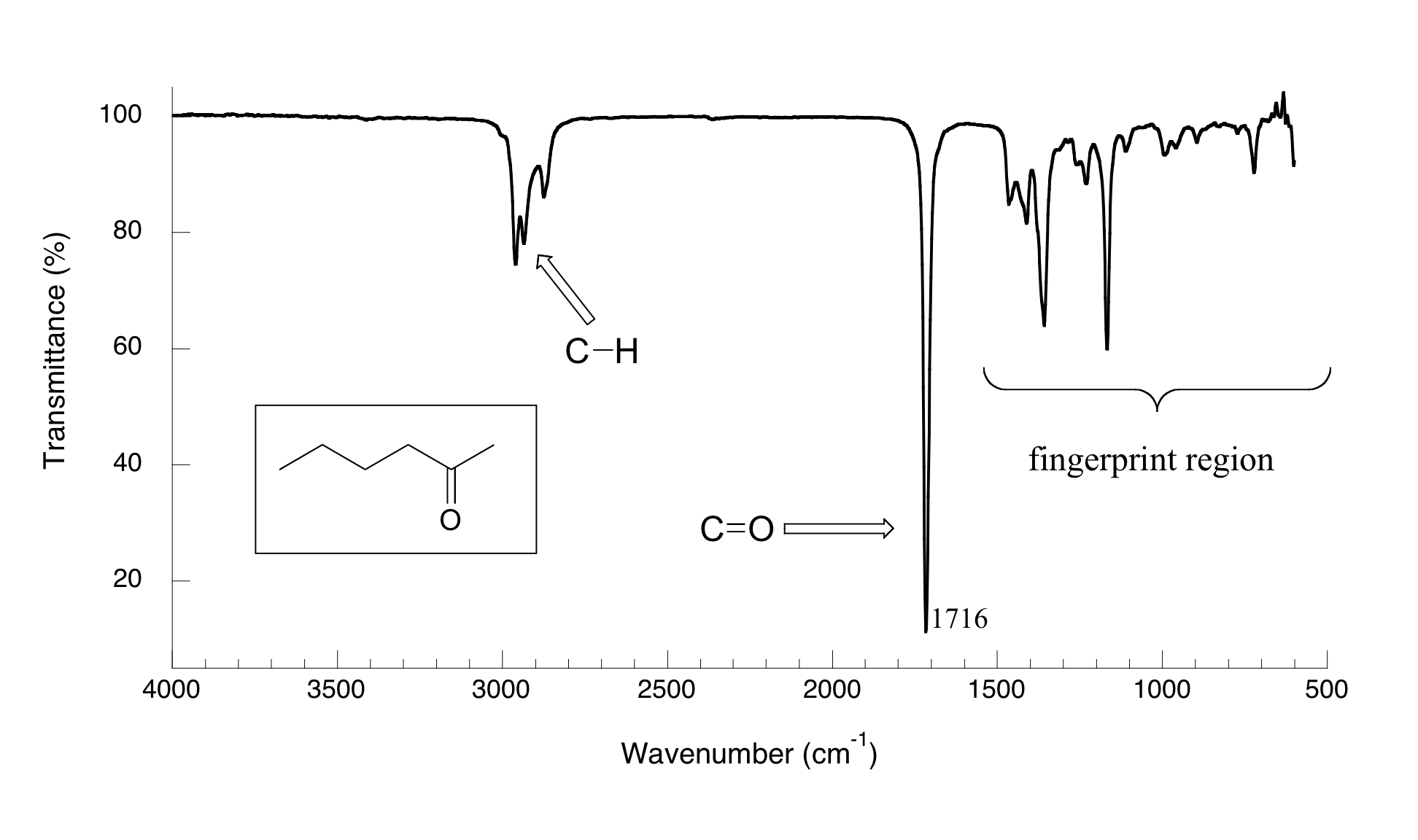
There are a number of things that need to be explained in order for you to understand what it is that we are looking at. On the horizontal axis we see IR wavelengths expressed in terms of a unit called wavenumber (cm-1), which tells us how many waves fit into one centimeter. On the vertical axis we see ‘% transmittance’, which tells us how strongly light was absorbed at each frequency (100% transmittance means no absorption occurred at that frequency). The solid line traces the values of % transmittance for every wavelength – the ‘peaks’ (which are actually pointing down) show regions of strong absorption. For some reason, it is typical in IR spectroscopy to report wavenumber values rather than wavelength (in meters) or frequency (in Hz). The ‘upside down’ vertical axis, with absorbance peaks pointing down rather than up, is also a curious convention in IR spectroscopy. We wouldn’t want to make things too easy for you!

