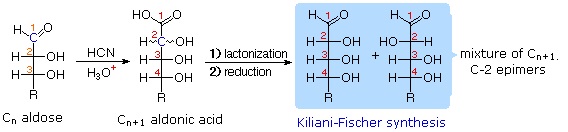
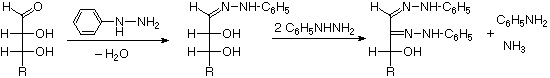22.8: Lengthening the Chain: The Kiliani-Fischer Synthesis
- Page ID
- 18289
Overview
Emil Fischer made use of several key reactions in the course of his carbohydrate studies. These are described here, together with the information that each delivers.
Oxidation
As noted above, sugars may be classified as reducing or non-reducing based on their reactivity with Tollens', Benedict's or Fehling's reagents. If a sugar is oxidized by these reagents it is called reducing, since the oxidant (Ag(+) or Cu(+2)) is reduced in the reaction, as evidenced by formation of a silver mirror or precipitation of cuprous oxide. The Tollens' test is commonly used to detect aldehyde functions; and because of the facile interconversion of ketoses and aldoses under the basic conditions of this test, ketoses such as fructose also react and are classified as reducing sugars.
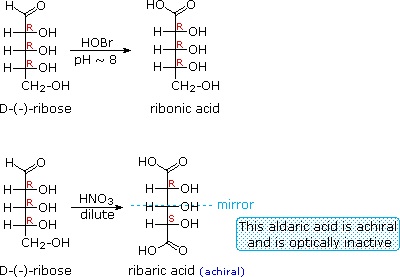
When the aldehyde function of an aldose is oxidized to a carboxylic acid the product is called an aldonic acid. Because of the 2º hydroxyl functions that are also present in these compounds, a mild oxidizing agent such as hypobromite must be used for this conversion (equation 1). If both ends of an aldose chain are oxidized to carboxylic acids the product is called an aldaric acid. By converting an aldose to its corresponding aldaric acid derivative, the ends of the chain become identical (this could also be accomplished by reducing the aldehyde to CH2OH, as noted below). Such an operation will disclose any latent symmetry in the remaining molecule. Thus, ribose, xylose, allose and galactose yield achiral aldaric acids which are, of course, not optically active. The ribose oxidation is shown in equation 2 below.
1. |
|
|
2. |
|
|
3. |
|
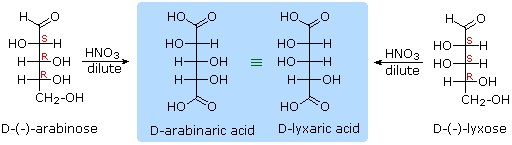
Other aldose sugars may give identical chiral aldaric acid products, implying a unique configurational relationship. The examples of arabinose and lyxose shown in equation 3 above illustrate this result. Remember, a Fischer projection formula may be rotated by 180º in the plane of projection without changing its configuration.
Reduction
Sodium borohydride reduction of an aldose makes the ends of the resulting alditol chain identical, HOCH2(CHOH)nCH2OH, thereby accomplishing the same configurational change produced by oxidation to an aldaric acid. Thus, allitol and galactitol from reduction of allose and galactose are achiral, and altrose and talose are reduced to the same chiral alditol. A summary of these redox reactions, and derivative nomenclature is given in the following table.
|
Derivatives of HOCH2(CHOH)nCHO |
||
|
HOBr Oxidation |
——> |
HOCH2(CHOH)nCO2H |
|
HNO3 Oxidation |
——> |
H2OC(CHOH)nCO2H |
|
NaBH4 Reduction |
——> |
HOCH2(CHOH)nCH2OH |
Osazone Formation
|
1. |
|
|
2. |
|
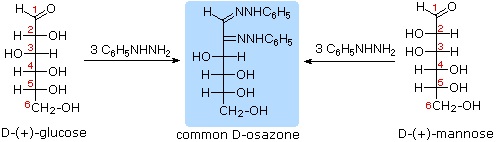
The osazone reaction was developed and used by Emil Fischer to identify aldose sugars differing in configuration only at the alpha-carbon. The upper equation shows the general form of the osazone reaction, which effects an alpha-carbon oxidation with formation of a bis-phenylhydrazone, known as an osazone. Application of the osazone reaction to D-glucose and D-mannose demonstrates that these compounds differ in configuration only at C-2.
Chain Shortening and Lengthening
|
1. |
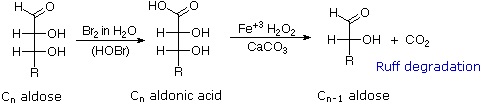 |
|
2. |
|
These two procedures permit an aldose of a given size to be related to homologous smaller and larger aldoses. The importance of these relationships may be seen in the array of aldose structures presented earlier, where the structural connections are given by the dashed blue lines. Thus Ruff degradation of the pentose arabinose gives the tetrose erythrose. Working in the opposite direction, a Kiliani-Fischer synthesis applied to arabinose gives a mixture of glucose and mannose. An alternative chain shortening procedure known as the Wohl degradation is essentially the reverse of the Kiliani-Fischer synthesis.
Fischer's train of logic in assigning the configuration of D-glucose
- Ribose and arabinose (two well known pentoses) both gave erythrose on Ruff degradation. As expected, Kiliani-Fischer synthesis applied to erythrose gave a mixture of ribose and arabinose.
- Oxidation of erythrose gave an achiral (optically inactive) aldaric acid. This defines the configuration of erythrose.
- Oxidation of ribose gave an achiral (optically inactive) aldaric acid. This defines the configuration of both ribose and arabinose.
- Ruff shortening of glucose gave arabinose, and Kiliani-Fischer synthesis applied to arabinose gave a mixture of glucose and mannose.
- Glucose and mannose are therefore epimers at C-2, a fact confirmed by the common product from their osazone reactions.
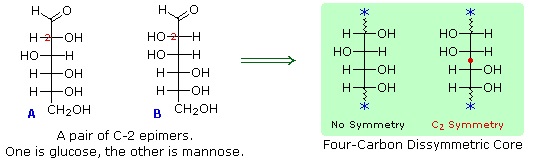
- A pair of structures for these epimers can be written, but which is glucose and which is mannose?
To determine which of these epimers was glucose, Fischer made use of the inherent C2 symmetry in the four-carbon dissymmetric core of one epimer (B). This is shown in the following diagram by a red dot where the symmetry axis passes through the projection formula. Because of this symmetry, if the aldehyde and 1º-alcohol functions at the ends of the chain are exchanged, epimer B would be unchanged; whereas A would be converted to a different compound.
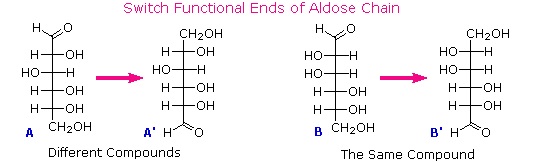
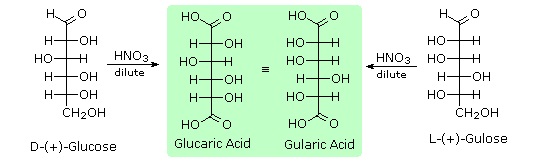
Fischer looked for and discovered a second aldohexose that represented the end group exchange for the epimer lacking the latent C2 symmetry (A). This compound was L-(+)-gulose, and its exchange relationship to D-(+)-glucose was demonstrated by oxidation to a common aldaric acid product. The remaining epimer is therefore mannose.
Contributors
Prof. Steven Farmer (Sonoma State University)
William Reusch, Professor Emeritus (Michigan State U.), Virtual Textbook of Organic Chemistry