2.2: Solutions to Selected Problems
- Page ID
- 238862
SM11. Solutions to Selected Problems
Problem SM1.1.

Problem SM1.2.
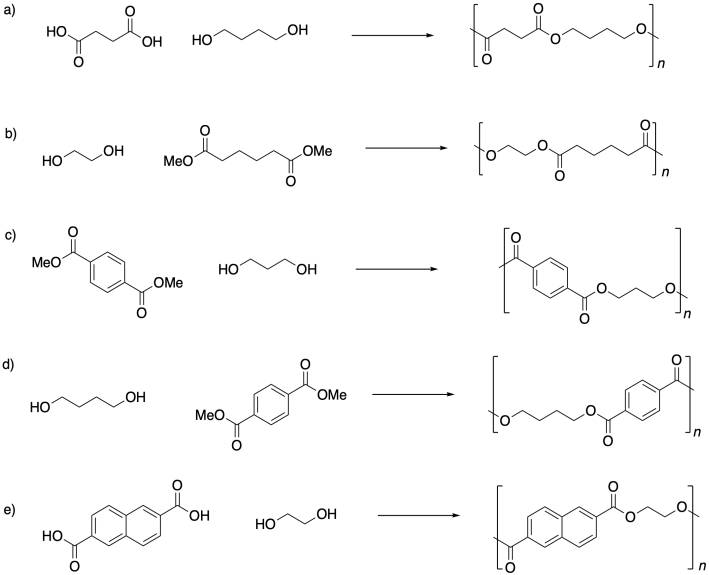
Problem SM1.3.
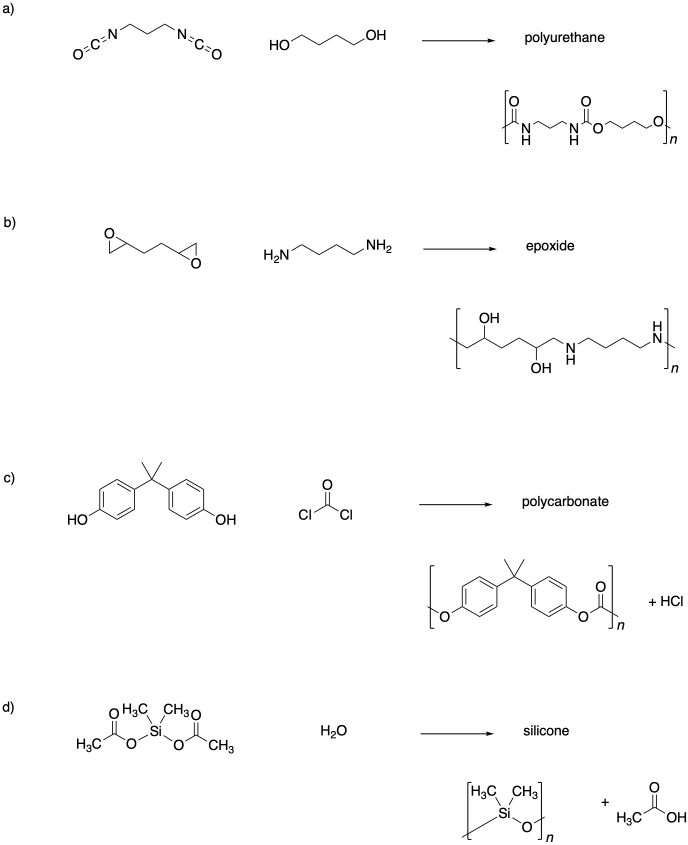
Problem SM1.4.
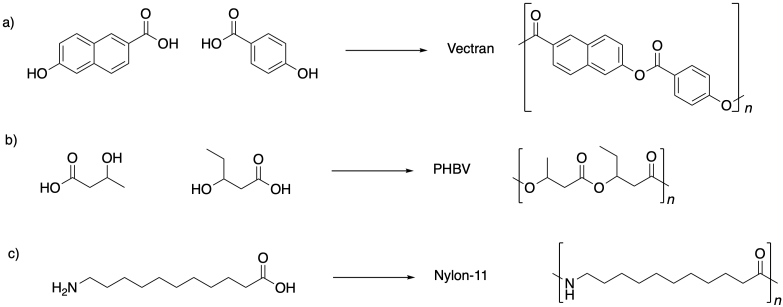
Problem SM1.5.
a) After seven steps, the polymer will be 27 = 128 units long; MW = 128 x 150 g/mol = 19,200 g/mol.
b) After sixteen steps, the polymer will be 216 = 65,536 units long; MW = [(120 + 130)/2] x 65,360 g/mol = 8,192,000 g/mol.
c) After ten steps, the polymer will be 210 = 1,024 units long; MW = [(100 + 105)/2] x 1,024 g/mol = 104,960 g/mol. One condensation will occur at the two ends of each monomer, except for the ones on the ends, but that's a loss of approximately 1,023 x 15 = 15,345 g/mol. The net molecular weight is 104,960 - 15,345 g/mol = 89,615 g/mol.
d) Chain growth occurs linearly, so the molecular weight is 30 x 105 g/mol + 65 g/mol (end group) = 3,215 g/mol.
Problem SM2.1.
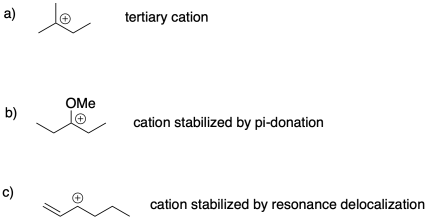
Problem SM2.2.
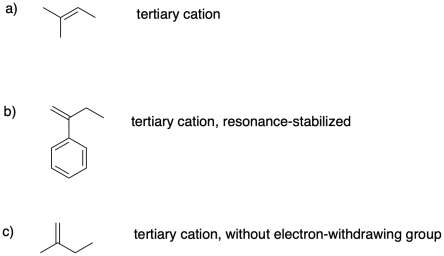
Problem SM2.3.

Problem SM2.4.
Problem SM2.5.
These large, highly charged anions are not very soluble, limiting their interaction with the growing polymer chains.
Problem SM3.1.
a) GaCl3
b) SnCl4
c) ZnCl2
d) FeCl3
Problem SM3.2.

Problem SM3.3.

Problem SM4.1.
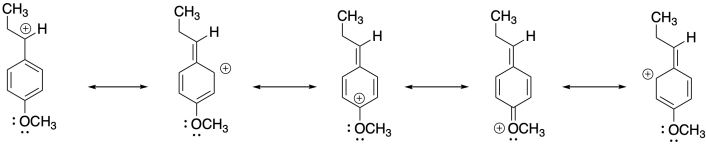
The additional resonance stabilization of the anion by the nitrile group makes anionic polymerization proceed smoothly.
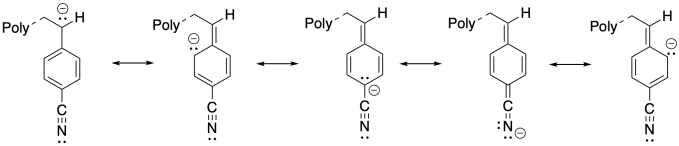
Problem SM4.2.
a) Vinyl chloride's electronegative chlorine might stabilize an anion on the adjacent carbon. However, that inductive effect may be offset by lone pair repulsion between carbon and chlorine.

b) Under these strongly basic conditions, 1,2-elimination may result from the growing polymer chain. Very basic conditions may even result in 1,2-elimination from viyl chloride to give acetylene (ethyne).
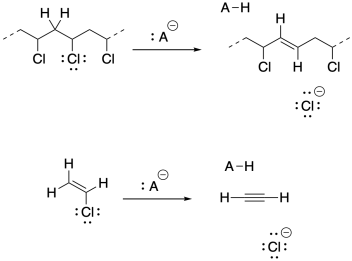
Problem SM5.1.
a) Li+, Na+, K+
b) Be2+, Mg2+, Ca2+
Problem SM5.2.
a) K+, Na+, Li+
b) Ca2+, Mg2+, Be2+
Problem SM5.3.
a) Et3Al
b) Et2Zn
c) Ph3B
d) (CH3O)2AlCH3
Problem SM6.1.

Problem SM6.2.
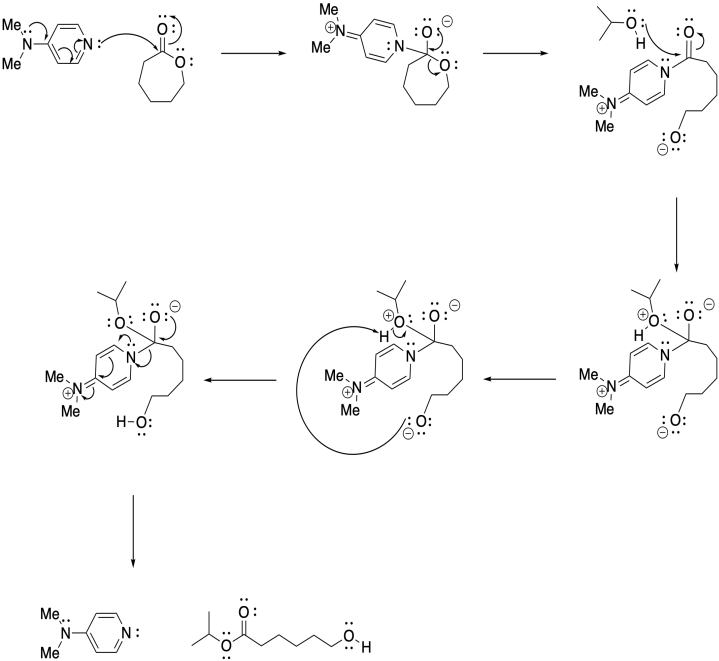
Problem SM6.3.

Problem SM7.1.
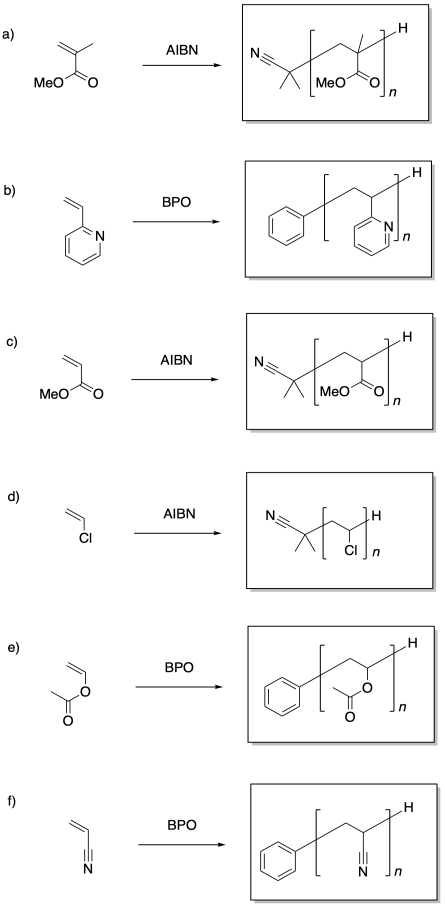
Problem SM7.2.

Problem SM7.3.
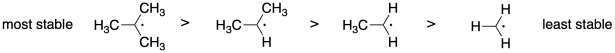
Problem SM8.1.
The more stable the radical, the more rapidly it will form from the monomer, leading to faster polymerization.
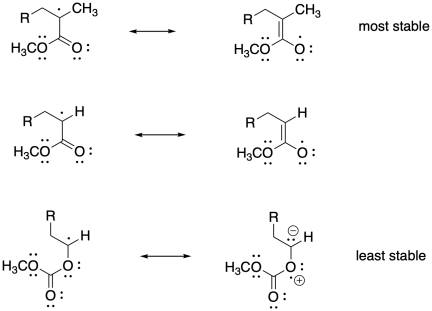
Problem SM8.2.
The more stable the radical generated upon fragmentation of R, the more the equilibrium will shift toward growing phase.
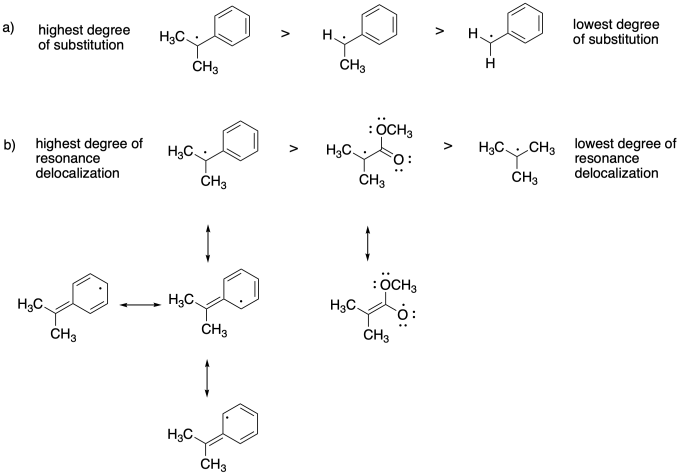
Problem SM8.3.
The more stable the radical formed, the more the equilibrium will shift toward the dormant phase.
Problem SM8.4.
a) With a fast-polymerizing monomer like this one, we need a chain control agent that will provide a similarly stable radical, so that there is an appreciable equilibrium allowing chains to move into the dormant phase; hence the phenyl substituent. However, to get into a new growing phase, we need an R group that fragments very easily, such as this disubstituted benzyl.
b) With a monomer on the lower end of radical stability, we need a chain transfer agent that isn't terribly stable as a radical, or else the chains will shift completely into the dormant phase. We also need an R group that will fragment at a rate comparable to the original radical chain, so we have one that will form a modestly stable radical.
Problem SM9.1.
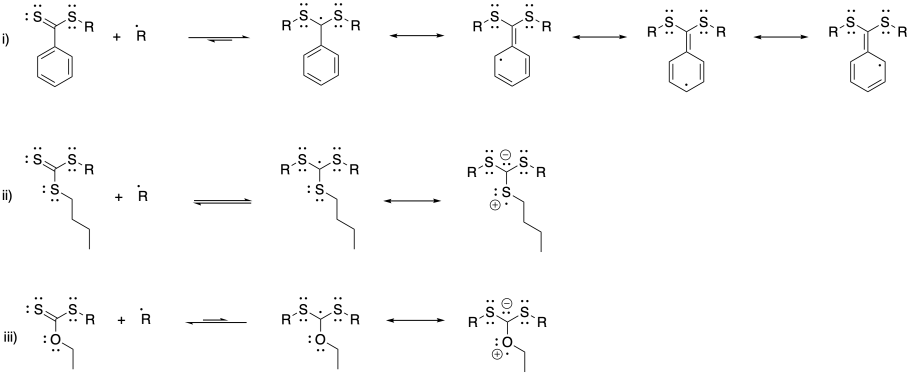
Problem SM9.2.
a)

b)

Problem SM9.3.

Problem SM9.4.
a)
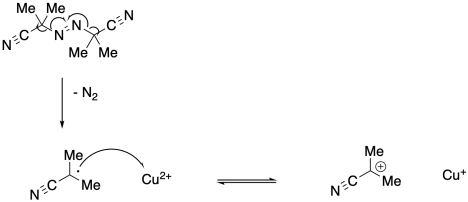
b) The radical generated in the first step may initiate new polymer chains instead.


