4.5: Extraction Theory
- Page ID
- 93533
Partition/Distribution Coefficient \(\left( K \right)\)
When a solution is placed in a separatory funnel and shaken with an immiscible solvent, solutes often dissolve in part into both layers. The components are said to "partition" between the two layers, or "distribute themselves" between the two layers. When equilibrium has established, the ratio of concentration of solute in each layer is constant for each system, and this can be represented by a value \(K\) (called the partition coefficient or distribution coefficient).
\[K = \dfrac{\text{Molarity in organic phase}}{\text{Molarity in aqueous phase}}\]
For example, morphine has a partition coefficient of roughly 6 in ethyl acetate and water.\(^2\) If dark circles represent morphine molecules, \(1.00 \: \text{g}\) of morphine would distribute itself as shown in Figure 4.11.
![Diagram of morphine beside diagram of separation. Image A: 50 milliliter ethyl acetate above 50 milliliter water in flask, black dots (representing morphine) dissolved in both. Below, equation reads K = [morphine]ethyl acetate / [morphine]water = 0.0600 Moles / 0.0101 Moles = 5.95. B: 25 milliliter ethyl acetate over 50 milliliter water in flask, black dots in both. Below, equation reads K = 0.105 moles over 0.0177 moles = 5.93.](https://chem.libretexts.org/@api/deki/files/126150/Nichols_Screenshot_4-4-1.png?revision=1)
Note that with equal volumes of organic and aqueous phases, the partition coefficient represents the ratio of particles in each layer (Figure 4.11a). When using equal volumes, a \(K\) of \(\sim 6\) means there will be six times as many morphine molecules in the organic layer as there are in the water layer. The particulate ratio is not as simple when the layer volumes are different, but the ratio of concentrations always equals the \(K\) (Figure 4.11b).
The partition coefficients reflect the solubility of a compound in the organic and aqueous layers, and so is dependent on the solvent system used. For example, morphine has a \(K\) of roughly 2 in petroleum ether and water, and a \(K\) of roughly 0.33 in diethyl ether and water.\(^2\) When the \(K\) is less than one, it means the compound partitions into the aqueous layer more than the organic layer.
Choosing a Solvent with Solubility Data
The partition coefficient \(K\) is the ratio of the compound's concentration in the organic layer compared to the aqueous layer. Actual partition coefficients are experimental, but can be estimated by using solubility data.
\[\begin{align} K &= \dfrac{\text{Molarity in organic phase}}{\text{Molarity in aqueous phase}} \\[4pt] & \approx \dfrac{\text{Solubility in organic phase}}{\text{Solubility in aqueous phase}} \end{align}\]
The \(K\)'s calculated using molarity and solubility values are not identical since different equilibria are involved. The true \(K\) represents the equilibrium between aqueous and organic solutions, while solubility data represent the equilibrium between a saturated solution and the solid phase. The two systems are related however, and \(K\)'s derived from solubility data should be similar to actual \(K\)'s.
| Solvent | 1 g caffene dissolves in solvent (at 25 °C) |
|---|---|
| water | 45 mL |
| Diethyl Ether | 530 mL |
| Benzene | 100 mL |
| Chloroform | 5.5 mL |
Solubility data can therefore be used to choose an appropriate solvent for an extraction. For example, imagine that caffeine (Figure 4.12) is intended to be extracted from tea grounds into boiling water, then later extracted into an organic solvent. Solubility data for caffeine is shown in Table 4.2.

Both diethyl ether and benzene at first glance appear to be poor choices for extraction because caffeine is more soluble in water than in either solvent (if a gram of caffeine dissolves in \(46 \: \text{mL}\) water, but \(100 \: \text{mL}\) of benzene, caffeine is more soluble in water). When extracting with either of these solvents, the \(K\) would be less than one (see calculation below) and it would be an "uphill battle" to draw out the caffeine from the water. However, caffeine is more soluble in chloroform than water, so chloroform would be the best choice of the solvents shown in terms of the maximum extraction of caffeine.
\[\begin{align} K_\text{benzene} &\sim \dfrac{\left( \dfrac{1 \: \text{g caffeine}}{100 \: \text{mL benzene}} \right)}{\left( \dfrac{1 \: \text{g caffeine}}{46 \: \text{mL water}} \right)} \sim 0.46 \\[4pt] K_\text{chloroform} &\sim \dfrac{\left( \dfrac{1 \: \text{g caffeine}}{5.5 \: \text{mL chloroform}} \right)}{\left( \dfrac{1 \: \text{g caffeine}}{46 \: \text{mL water}} \right)} \sim 8.4 \end{align}\]
Another consideration when choosing a solvent for extraction is toxicity: chloroform is carcinogenic and therefore is probably not the best option despite its excellent solvation ability. A further consideration is the solubility of other components present in a mixture. If the goal is to extract caffeine preferentially and leave behind other components in the tea, one solvent may be more selective in this regard.
Quantitating Single Extraction
Hyoscyamine is an alkaloid from a plant in the nightshade family (Figure 4.13a), and is used medicinally to provide relief for a variety of gastrointestinal disorders. Its solubility data is shown in Figure 4.13b.
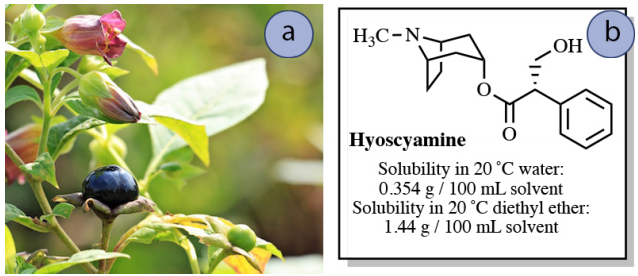
Imagine that a nearly saturated solution of \(0.50 \: \text{g}\) hyoscyamine in \(150 \: \text{mL}\) water is to be extracted into \(150 \: \text{mL}\) diethyl ether. How much hyoscyamine would be extracted into the diethyl ether layer in this process?
This quantity can be approximated using the solubility data. Taking the ratio of the compound's solubility in diethyl ether compared to water gives an approximate \(K\) of 4.
\[\begin{align} K &\sim \dfrac{\text{organic solubility}}{\text{water solubility}} \\[4pt] &\sim \dfrac{\left( 1.44 \: \text{g hyoscyamine}/100 \: \text{mL diethyl ether} \right)}{\left( 0.354 \: \text{g hyoscyamine}/100 \: \text{mL water} \right)} \\[4pt] &\sim \textbf{4.07} \: \text{(approximate} K \text{)} \end{align}\]
If "\(x\)" is the gram quantity of hyoscyamine extracted into the diethyl ether layer, then "\(0.50 \: \text{g} - x\)" would remain in the aqueous layer after equilibrium is established. Knowing the value of \(K\), the value of \(x\) can be solved for using the equation below.
\[4.07 = \dfrac{\left( \dfrac{x}{150 \: \text{mL ether}} \right)}{\left( \dfrac{0.50 \: \text{g} - x}{150 \: \text{mL water}} \right)}\]
After solving the algebra, \(x = \textbf{0.40 g}\). This result means that \(0.40 \: \text{g}\) of the original \(0.50 \: \text{g}\) of hyoscyamine is extracted into the diethyl ether using a single extraction. This process is summarized in Figure 4.14.
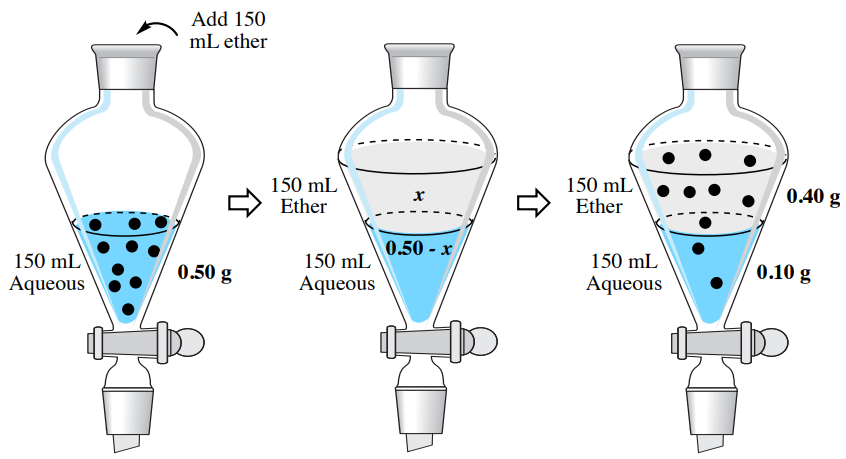
In this example, a single extraction resulted in extraction of \(80\%\) of the hyoscyamine \(\left( 100\% \times 0.40 \: \text{g}/0.50 \: \text{g} \right)\) from the aqueous layer into the organic layer. The partitioning of the compound between the two layers caused the sample to be incompletely extracted.
Multiple Extractions
Overview of Multiple Extractions
Depending on the partition coefficient for a compound in a solvent, a single extraction may be all that is needed to effectively extract a compound. However, more often than not a procedure calls for a solution to be extracted multiple times in order to isolate a desired compound, as this method is more efficient than a single extraction (see journal article in Figure 4.15b for an example of where this process is used).

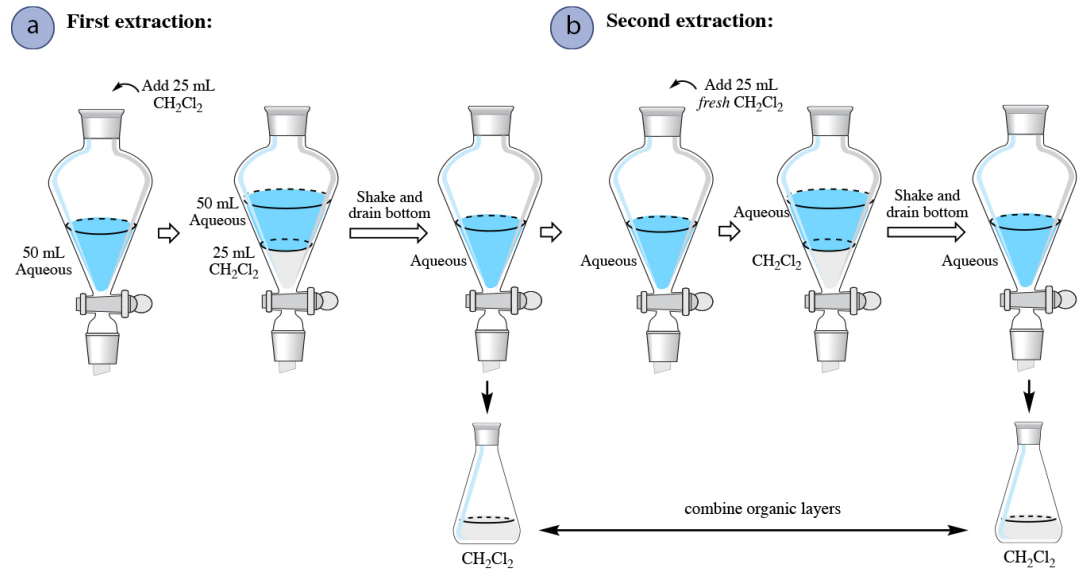
In a multiple extraction procedure, a quantity of solvent is used to extract one layer (often the aqueous layer) multiple times in succession. The extraction is repeated two to three times, or perhaps more times if the compound has a low partition coefficient in the organic solvent. Figure 4.16 shows a diagram of an aqueous solution being extracted twice with diethyl ether. Diethyl ether has a density less than \(1 \: \text{g/mL}\), so is the top organic layer in the funnel.

In a multiple extraction of an aqueous layer, the first extraction is procedurally identical to a single extraction. In the second extraction, the aqueous layer from the first extraction is returned to the separatory funnel (Figure 4.16b), with the goal of extracting additional compound. Since the organic layer from the first extraction had already reached equilibrium with the aqueous layer, it would do little good to return it to the separatory funnel and expose it to the aqueous layer again. Instead, fresh diethyl ether is added to the aqueous layer, since it has the potential to extract more compound.
The process is often repeated with a third extraction (not shown in Figure 4.16), with the aqueous layer from the second extraction being returned to the separatory funnel, followed by another portion of fresh organic solvent. In multiple extractions, the organic layers are combined together,as the goal is to extract the compound into the organic solvent.
When an aqueous solution is extracted with an organic solvent that is denser than water (for example dichloromethane, \(\ce{CH_2Cl_2}\)), the only procedural difference is that there is no need to ever drain the aqueous layer from the separatory funnel. After draining the organic layer from the first extraction, fresh solvent can be added to the aqueous layer remaining in the funnel to begin the second extraction (Figure 4.17b).
Quantitating Multiple Extraction
To demonstrate the effectiveness of a multiple extraction, let's return to the problem from the single extraction section, where a solution of \(0.50 \: \text{g}\) hyoscyamine in \(150 \: \text{mL}\) water is to be extracted into diethyl ether. Instead of using one \(150 \: \text{mL}\) portion, let's instead split the solvent into three \(50 \: \text{mL}\) portions of diethyl ether. How much hyoscyamine would be extracted with this method?
In the previous section, solubility data was used to estimate the partition coefficient \(K\), and it was found to be 4.07. As before, we can assign the quantity of hyoscyamine extracted into the diethyl ether the value "\(x\)", which would leave "\(0.50 \: \text{g} - x\)" remaining in the aqueous layer of the first extraction. Using \(K\), the calculation is identical to the previous discussion, differing only in the smaller volume of the organic layer (\(50 \: \text{mL}\) instead of \(150 \: \text{mL}\)).
\[4.07 = \dfrac{\left( \dfrac{x}{50 \: \text{mL ether}} \right)}{\left( \dfrac{0.50 \: \text{g} - x}{150 \: \text{mL water}} \right)}\]
After solving the algebra, \(x = 0.29 \: \text{g}\). This result means that \(0.29 \: \text{g}\) is extracted into the diethyl ether in the first extraction and \(0.21 \: \text{g}\) remains in the aqueous layer \(\left( 0.50 \: \text{g} - 0.29 \: \text{g} \right)\). As the aqueous layer is returned to the separatory funnel, the residual \(0.21 \: \text{g}\) is the quantity to be further extracted, which alters the calculation for the second extraction by replacing the \(0.50 \: \text{g}\) value.
\[4.07 = \dfrac{\left( \dfrac{x}{50 \: \text{mL ether}} \right)}{\left( \dfrac{0.21 \: \text{g} - x}{150 \: \text{mL water}} \right)}\]
After solving the algebra, \(x = 0.12 \: \text{g}\). This result means that \(0.12 \: \text{g}\) is extracted into the diethyl ether in the second extraction and \(0.09 \: \text{g}\) remains in the aqueous layer \(\left( 0.21 \: \text{g} - 0.12 \: \text{g} \right)\). The calculation for the third extraction is as follows:
\[4.07 = \dfrac{\left( \dfrac{x}{50 \: \text{mL ether}} \right)}{\left( \dfrac{0.09 \: \text{g} - x}{150 \: \text{mL water}} \right)}\]
After solving the algebra, \(x = 0.05 \: \text{g}\). This result means \(0.04 \: \text{g}\) remains in the aqueous layer \(\left( 0.09 \: \text{g} - 0.05 \: \text{g} \right)\) after the third extraction. The results of the calculations in this section are summarized in Figure 4.18.
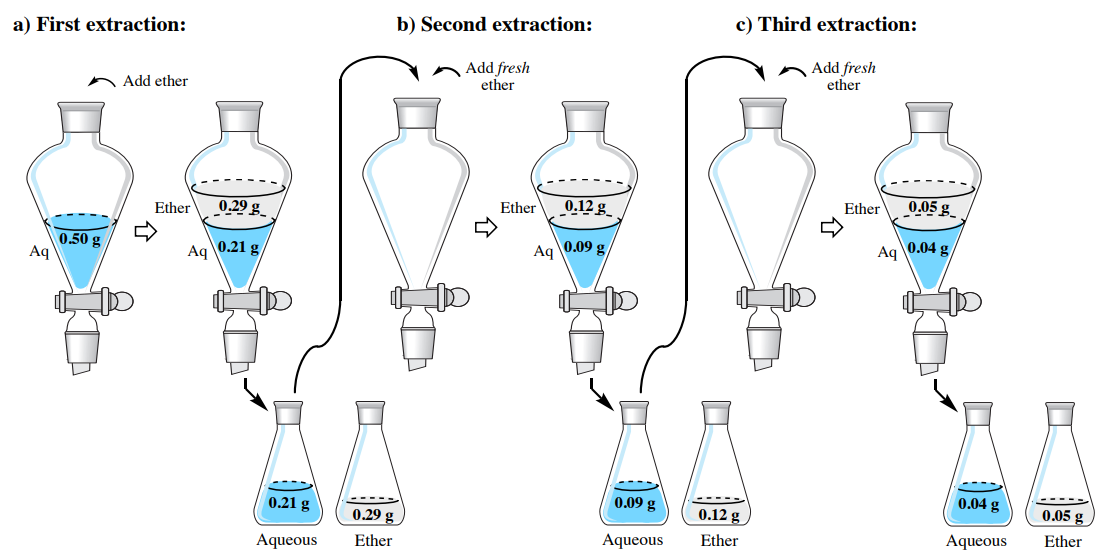
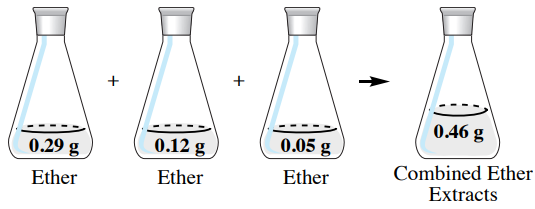
If the \(50 \: \text{mL}\) diethyl ether extracts are combined in this example (Figure 4.19), there would be a total of \(0.46 \: \text{g}\) of hyoscyamine in the combined organic extracts. Of the \(0.50 \: \text{g}\) of hyoscyamine in the original aqueous layer, \(92\%\) of the material is extracted into the organic layer \(\left( 100\% \times 0.46 \: \text{g}/0.50 \: \text{g} \right)\). This is a greater quantity than was obtained using a single extraction of \(150 \: \text{mL}\) diethyl ether, which resulted in only \(0.40 \: \text{g}\) of hyoscyamine extracted (\(80\%\)).
These calculations demonstrate that using multiple portions of a solvent maximizes the extractive power of the solvent. In general, three extractions are the optimal compromise between expended effort and maximizing the recovery of material.
\(^2\)The partition coefficients were approximated using solubility data found in: A. Seidell, Solubilities of Inorganic and Organic Substances, D. Van. Nostrand Company, 1907.
\(^3\)From: The Merck Index, 12\(^\text{th}\) edition, Merck Research Laboratories, 1996.


