2.2: Bredt's Rule
- Page ID
- 21829
In its original form, Bredt's Rule stated that bridged ring systems (like camphane (Figure 1.2.1.1A) and pinane (Figure 1.2.1.1B)) (Fig 1.2.1.1) cannot have a double bond at the bridgehead position (the points marked by bold dots in structures ‘A’ and ‘B’). This rule came from observations on dehydration of alcohols in these ring systems. When you look at these molecules carefully, you could see that the bridged rings are made out of a larger ring (shown by thick lines in the Figure s) bearing a bridge at specified points. Most of the rings studied by Bredt had six-membered ring as the largest ring. The constraint dictated by Bredt's Rule has now been attributed to the fact that the small and common rings can accommodate only a cis- double bond. A bridgehead olefin demands a trans- geometry at the olefin. Hence the rule was applicable to almost all naturally occurring bridged ring systems known at that time.
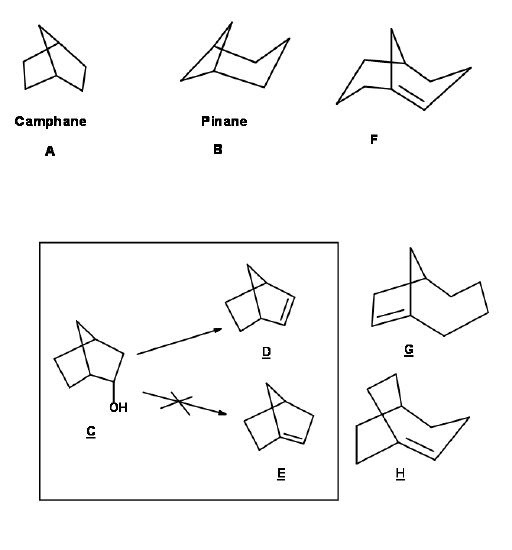
The scope of this rule has been investigated in detail. Medium sized rings are large enough to accommodate a trans- double bond. Hence the bicyclic rings 1.2.1.1F and 1.2.1.1G, bearing a cyclooctane ring as the outer ring, were synthesized and were indeed found to be stable. On the other hand, the isomeric cycloheptene ring system 1.2.1.1H was unstable. Faweet (1950) suggested that the S value, which is a summation of the numbers found in the nomenclature (m + n + o = S), would determine the stability of the ring system. Bicyclic ring systems with a bridgehead double bond having S value less than 9 would be highly strained. As the S value increases, the strain decreases.
Bretd’s Rule cautions us on the type of rings that could bear a double bond. When a synthetic intermediate or a transition state in a mechanism demands such an intermediate, one should exercise caution on the position of the olefin. For example, Prelog (1948, 1949) attempted an aldol condensation on the ring systems shown (Fig 1.2.1.2). When n = 5, both products bicyclo[6,4,0]alkene (S = 10) (C), and
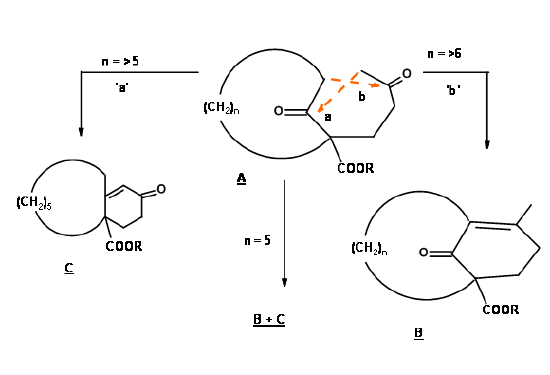
Fig 1.2.1.2
bicyclo[5,3,1]alkene (S=9) (B) were formed. On the other hand, when n=>6, the main product was a bicyclo[6,3,1]alkene system (B) (S=10). When n = <5 product B was not observed. Note that these models were based on reversible aldol condensation reactions (equilibrium reactions) and therefore correspond to the thermodynamic stability of the product. Under forced conditions however, the rule may not hold, as seen in the following example (Fig 1.2.1.3).
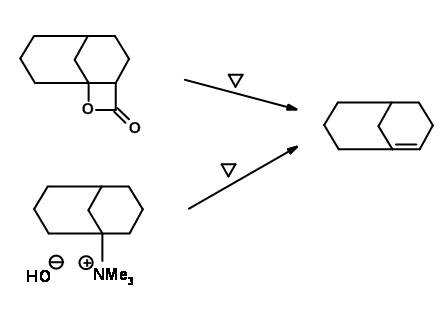
Fig 1.2.1.3


