21.12: Evidence Bearing on the Mechanism of [2 + 2] Cycloadditions
- Page ID
- 22321
We have not given you much evidence to decide why it is that some thermal [2 + 2] cycloadditions occur but not others. What is special about fluoroalkenes, allenes, and ketenes in these reactions? One possibility is that Mobius rather than the Huckel transition states are involved, but the Mobius transition states are expected to suffer from steric hindrance (Section 21-10B). It is also possible that [2 + 2] cycloadditions, unlike the Diels-Alder additions, proceed by stepwise mechanisms. This possibility is strongly supported by the fact that these reactions generally are not stereospecific. Thus with tetrafluoroethene and trans,trans-2,5-hexadiene two products are formed, which differ in that the 1-propenyl group is trans to the methyl group in one adduct, \(45\), and cis in the other, \(46\):
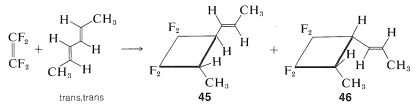
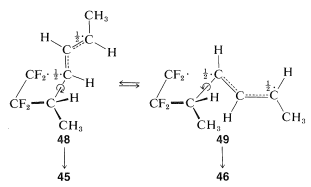
A stepwise reaction involving a biradical intermediate accounts for the formation of both \(45\) and\(46\). In the biradical mechanism the first step is formation of just one \(\ce{C-C}\) bond between the reactants, and this could occur in two different ways to give \(47\) or \(48ab\):

Of these, \(48ab\) is predicted to have substantial electron delocalization because of the nearly equivalent VB structures \(48a\) and \(48b\). By the simple MO theory \(48ab\) should have a delocalization energy of \(16 \: \text{kcal mol}^{-1}\) (Section 21-5B). The biradical \(47\) has no comparable electron delocalization and would be expected to be formed much less readily.
Collapse of \(48\) through formation of the second \(\ce{C-C}\) bond would give \(45\) and an overall stereospecific addition. However, rotation around the \(\ce{C-C}\) single bond of \(48\) forms a different radical conformation, \(49\), which would collapse to the other stereoisomer, \(46\):
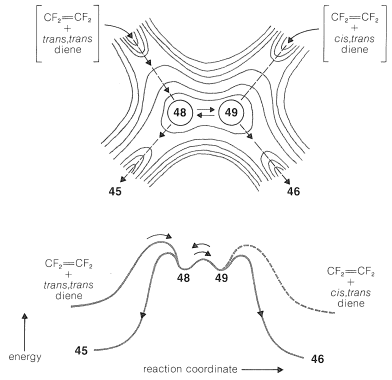
If the reaction is stepwise, why is it stepwise? In the first place, as we have seen (Section 21-10A), there are theoretical reasons why [2 + 2] cycloadditions may not occur in a concerted manner. Second, there are thermodynamic reasons why some alkenes undergo stepwise [2 + 2] additions and others do not. Regarding the second point, we can estimate that \(2 \ce{CH_2=CH_2} \rightarrow \cdot \ce{CH_2-CH_2-CH_2-CH_2} \cdot\) has \(\Delta H^0 \sim 37 \: \text{kcal}\), which is too high to achieve at a useful rate at those temperatures where the equilibrium constant is favorable for cyclobutane formation. In other words, when \(K_\text{eq}\) is favorable, the rate is too slow, and when the rate is fast enough, \(K_\text{eq}\) is unfavorable. In contrast, \(2 \ce{CF_2=CF_2} \rightarrow \cdot \ce{CF_2-CF_2-CF_2-CF_2} \cdot\) is estimated to have \(\Delta H^0 = -7 \: \text{kcal}\)! This tells us that \(\ce{CF_2=CF_2}\) has an abnormally low \(\ce{C=C}\) \(\pi\)-bond energy and, in fact, \(\Delta H^0\) for addition of hydrogen to one mole of tetrafluoroethene \(\left( -55 \: \text{kcal} \right)\) is \(22 \: \text{kcal}\) more negative than \(\Delta H^0\) for ethene \(\left( -33 \: \text{kcal} \right)\). If formation of \(\cdot \ce{CF_2-CF_2-CF_2-CF_2} \cdot\) from \(2 \ce{CF_2=CF_2}\) actually is exothermic, then it may seem surprising that \(\ce{CF_2=CF_2}\) can be kept in a container without immediately reacting with itself. That it can is because fairly high-energy collisions are required to overcome the nonbonded repulsions that resist bringing the carbons close enough together to permit the formation of the biradical. Nonetheless, \(\ce{CF_2=CF_2}\) generally is regarded as a hazardous and unpredictable chemical by virtue of its unusually low \(\ce{C=C}\) \(\pi\)-bond strength.
1,2-Propadiene also appears to have the potential for much easier formation of a biradical than does ethene. Not all [2 + 2] cycloadditions proceed by biradical mechanisms, some clearly occur by stepwise reactions involving ionic intermediates.
Contributors and Attributions
John D. Robert and Marjorie C. Caserio (1977) Basic Principles of Organic Chemistry, second edition. W. A. Benjamin, Inc. , Menlo Park, CA. ISBN 0-8053-8329-8. This content is copyrighted under the following conditions, "You are granted permission for individual, educational, research and non-commercial reproduction, distribution, display and performance of this work in any format."


