21.10: Hückel's 4n + 2 Rule
- Page ID
- 22319
Cyclobutadiene and Cyclooctatetraene
More than 100 years ago, Kekule recognized the possible existence of other conjugated cyclic polyalkenes, which at least superficially would be expected to have properties like benzene. The most interesting of these are cyclobutadiene, \(23\), and cyclooctatetraene, \(24\):

For each we can write two equivalent planar VB structures, and the qualitative VB method would suggest that both compounds, like benzene, have substantial electron-delocalization energies. However, the planar structures would have abnormal \(\ce{C-C=C}\) angles, and consequently at least some degree of destabilization associated with these bond angles (Section 12-7). Nonetheless, estimation of the strain energies show that while they are substantial, they are not prohibitive. Should then these molecules be stabilized by resonance in the same sense as benzene is postulated to be?
In 1911 a German chemist, R. Willstatter (Nobel Prize 1915), reported an extraordinary thirteen-step synthesis of cyclooctatetraene from a rare alkaloid called pseudopelletierine isolated from the bark of pomegranate trees. The product was reported to be a light-yellow, highly unsaturated compound that absorbed four moles of hydrogen to form cyclooctane. Numerous tries to repeat the Willstatter synthesis were unsuccessful, and in the 1930s the prevailing opinion was that the product had been misidentified. However, during the Second World War, the German chemist W. Reppe found that cyclooctatetraene can be made in reasonable yields by the tetramerization of ethyne under the influence of a nickel cyanide catalyst:

The properties of the product substantiated Willstatter's reports and it became clear that cyclooctatetraene is not like benzene.
Subsequent studies of the geometry of the molecule revealed further that it is nonplanar, with alternating single and double bonds, \(25a\):
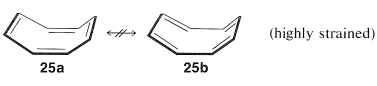
This geometry precludes the possibility of two equivalent VB structures, as for benzene, because, as you will see if you try to make a ball-and-stick model, \(25b\) is highly strained and not energetically equivalent to \(25a\) at all. Thus we can conclude that the delocalization energy of cyclooctatetraene is not large enough to overcome the angle strain that would develop if the molecule were to become planar and allow the \(\pi\) electrons to form equivalent \(\pi\) bonds between all of the pairs of adjacent carbons.
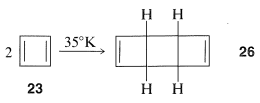
Cyclobutadiene, \(23\), eluded Kekule, Willstatter, and a host of other investigators for almost 100 years. As more work was done, it became increasingly clear that the molecule, when formed in reactions, was immediately converted to something else. Finally, the will-o'-the-wisp was captured in an essentially rigid matrix of argon at \(8 \: \text{K}\). It was characterized by its spectral properties (not by combustion analysis). On warming to even \(35 \: \text{K}\), it dimerizes to yield \(26\):
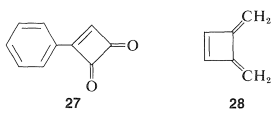
One possibility for the lack of stability\(^4\) of cyclobutadiene is that the angle strain associated with having four \(sp^2\) carbons in a four-membered ring is much greater than estimated. However, the stable existence of many compounds with four such \(sp^2\) carbons, for example \(27\) and \(28\), make this argument weak, if not invalid:
Why, then, is cyclobutadiene so unstable and reactive? On this point, and also with respect to the nonaromatic character of cyclooctatetraene, the simple qualitative VB method that we have outlined is no help whatsoever. There is no way simply to look at the electron-pairing schemes \(23\) and \(24\) and see any difference between them and the corresponding schemes for benzene.\(^5\)
It is in this area that qualitative MO procedures have great success because there are general characteristics of the \(\pi\) molecular orbitals of monocyclic, conjugated polyene systems that predict differences in the properties of cyclobutadiene, benzene, cyclooctatetraene, and other similar compounds that are not obvious from the simple VB method.
As a rule, for \(N\) parallel atomic \(p\) orbitals overlapping in the \(\pi\) manner in a monocyclic array, there will be just one lowest molecular orbital, with all the atomic orbitals having the same phase. This will be seen for benzene in Figure 21-5. What is harder to understand without going through the calculations is that the higher-energy molecular orbitals for cyclic conjugated polyenes are predicted to come in successive degenerate\(^6\) pairs, as shown in Figure 21-13 for \(N = 3\) to \(9\).
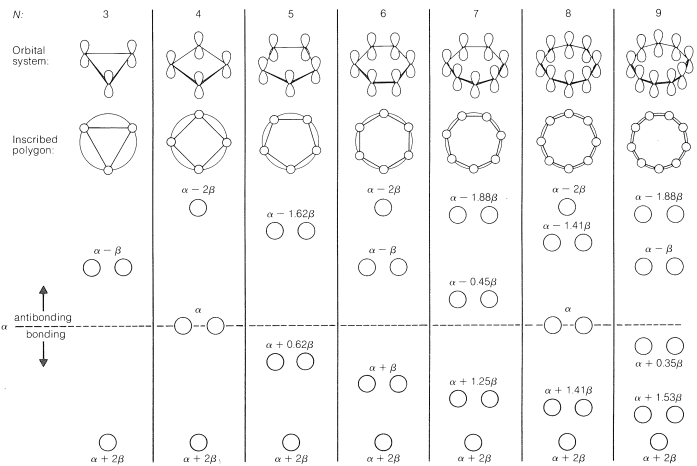
The qualitative ordering and, indeed, the numerical values of the energies of the \(\pi\) molecular orbitals for a cyclic system of \(N\) \(p\) orbitals can be derived in a very simple way. It is necessary only to inscribe a regular polygon with \(N\) sides inside a circle of radius \(2 \beta\) with a corner down. For example, for \(N = 5\) we get the following:
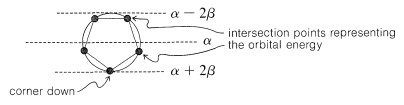
The molecular orbital energies are in units of \(\beta\) at the corners of the polygon. The nonbonding level corresponds to the horizontal dashed line drawn through the center of the circle.
The data of Figure 21-13 provide a rationale for the instability of cyclobutadiene and cyclooctatetraene. For cyclobutadiene, we can calculate that four \(\pi\) electrons in the lowest orbitals will lead to a predicted \(\pi\)-electron energy of \(2 \left( \alpha + 2 \beta \right) + 2 \left( \alpha \right) = 4 \alpha + 4 \beta\), which is just the \(\pi\)-electron energy calculated for two ethene bonds (see Figure 21-3). The delocalization energy of the \(\pi\) electrons of cyclobutadiene therefore is predicted to be zero!
Another feature of the \(\pi\) system of cyclobutadiene is that the four \(\pi\) electrons do not suffice to fill the three lowest orbitals and, if we apply Hund's rule (Section 6-1), the best way to arrange the electrons is as in \(29\), with two unpaired electrons, which is known as a triplet state:\(^7\)
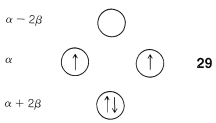
With the MO predictions of zero delocalization energy and an electronic configuration with unpaired electrons, we should not be surprised that cyclobutadiene readily dimerizes to give \(26\) even at very low temperatures.
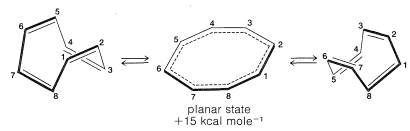
The energies of the molecular orbitals calculated for planar cyclooctatetraene (Figure 21-13) lead to a predicted delocalization energy of \(\left( 8 \alpha + 9.64 \beta \right) - \left( 8 \alpha + 8 \beta \right) = 1.64 \beta\) \(\left( \sim 31 \: \text{kcal} \right)\), which is smaller than that of benzene, even though there are eight atomic orbitals instead of six through which the electrons are delocalized. Furthermore, the lowest electronic configuration for the planar molecule is, like cyclobutadiene, predicted to be a triplet. Experimental evidence indicates that the positions of the double bonds of cyclooctatetraene shift slowly as the result of formation of the molecule in the unstable planar state. The energy input required to flatten the molecule is about \(15 \: \text{kcal mol}^{-1}\):
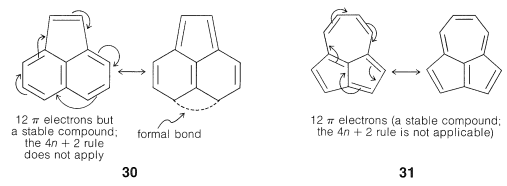
As Huckel formulated, the \(4n + 2\) rule applies only to monocyclic systems. However, as a practical matter it can be used to predict the properties of polycyclic conjugated polyenes, provided the important VB structures involve only the perimeter double bonds, as in the following examples:

Application of the \(4n + 2\) rule to other \(\pi\) systems, such as \(30\) and \(31\), is not valid because good VB structures cannot be written that involve changes in the pairing schemes of the perimeter electrons all at once.
Application of Resonance and of the \(4n + 2\) Rule to Cyclic Ions
The hydrogens of the \(\ce{-CH_2}-\) group of 1,3-cyclopentadiene are acidic. In fact, they are considerably more acidic than the ethyne hydrogens of the 1-alkynes (Section 11-8). This means that 1,3-cyclopentadiene is at least \(10^{30}\) times more acidic than the ordinary alkanes. The reason is that loss of one of the \(\ce{CH_2}\) protons of cyclopentadiene results in formation of an especially stabilized anion:
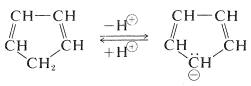
The structure of the anion may be described as a hybrid of five energetically equivalent structures, \(34a\) through (34e). The unshared electron pair therefore is delocalized over five carbon atoms, and the resulting delocalized anion is much more stable than expected for any one of the equivalent localized structures:
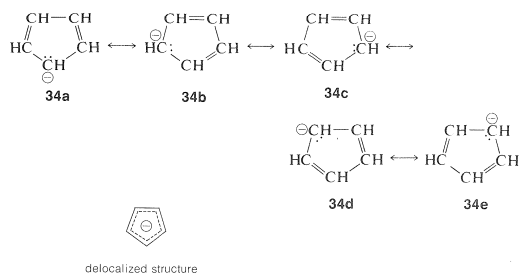
This looks very reasonable, although the simple beauty is seemingly destroyed by the fact that the cyclopentadienyl cation is not very stable, despite the five structures, \(35a\) through \(35e\), that may be written for it:
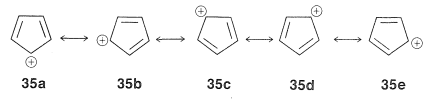
Extension of these ideas to the other ring sizes of Figure 21-13 suggests that all of the following ions, which have \(\left( 4n + 2 \right)\) \(\pi\) electrons, should be unusually stable:
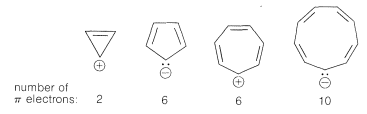
In contrast, the following should be unstable with \(4n\) \(\pi\) electrons and triplet electronic configurations:

These predictions indeed are borne out by many experiments, some of which we will discuss later.
\(^4\)It should be recognized that the term "stability" is subject to many interpretations. One criterion of stability would be whether an isolated molecule would fragment spontaneously in interstellar space, such as one would expect for a "molecule" consisting of two neon atoms \(1.5 \: \text{Å}\) apart (see Figure 4-6). A different criterion would be whether a molecule could be preserved in the presence of the same or other kinds of molecules at some specified temperature. The classical criterion would be whether the substance could be isolated, put into a bottle and preserved for at least a short time. All of the existing evidence indicates that cyclobutadiene molecules would not spontaneously decompose in interstellar space, but they do react with each other extremely readily, even at low temperatures, and can be preserved only by being held isolated from one another in a rigid matrix of a very inert material, such as solid argon. "Stability" in the sense of "lack of reactivity" has to be carefully defined in terms of experimental conditions. For example, 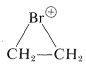 is very unstable in the presence of nucleophiles such as water or methanol, whereas it is quite stable in "super-acid solutions" where no good nucleophiles are present (Section 10-3B).
is very unstable in the presence of nucleophiles such as water or methanol, whereas it is quite stable in "super-acid solutions" where no good nucleophiles are present (Section 10-3B).
\(^5\)A rather simple extension of the VB method by what is called the "orbital-phase continuity principle" does permit the qualitative judgment that cyclobutadiene should be less stable than benzene [see W. A. Goddard III, J. Amer. Chem. Soc. 94, 743 (1972), for applications to many processes for which VB theory generally has been regarded as incapable of giving much insight].
\(^6\)Degenerate orbitals have the same energy; see Section 6-1.
\(^7\)The name "triplet state" is used because a system with two unpaired electrons has three different energy states in a magnetic field.
Contributors and Attributions
John D. Robert and Marjorie C. Caserio (1977) Basic Principles of Organic Chemistry, second edition. W. A. Benjamin, Inc. , Menlo Park, CA. ISBN 0-8053-8329-8. This content is copyrighted under the following conditions, "You are granted permission for individual, educational, research and non-commercial reproduction, distribution, display and performance of this work in any format."


