21.2: Characteristics of Simple Covalent Bonds
- Page ID
- 22311
The simplest kind of bond is that between univalent atoms in diatomic molecules, such as \(\ce{H_2}\), \(\ce{F_2}\), and so on. In the gas phase the molecules are in rapid motion, colliding with one another and the walls of the container. The atoms vibrate with respect to one another, and the molecules have rotational energy as well. Despite this activity, we can assign an average equilibrium bond distance \(\left( r_e \right)\) and an average bond energy \(\left( D_e \right)\) for normal, unexcited molecules. From ab initio calculations (Section 6-6), we learn that the energy of an \(\ce{H_2}\) molecule is a function of \(r\), the distance between the hydrogens, as shown in Figure 21-1.
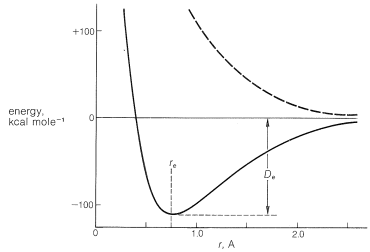
When the distance is reduced from \(r_e\), the energy increases very rapidly because of internuclear repulsion. As the separation between the atoms increases, the energy of the system increases more slowly and finally approaches that of the entirely free atoms.
The distance \(r_e\), which corresponds to the bond length at minimum energy, increases with atomic number downward in a column of the periodic table as the atoms get larger. It decreases across a horizontal row of the periodic table as the electronegativity of the atoms increases and the atomic radius becomes smaller. Other things being equal, the stronger the bond is, the shorter \(r_e\) will be, because a strong bond overcomes the repulsive forces between the nuclei and thus permits them to move closer together. For bonds between two carbon atoms, \(r_e\) usually ranges between about \(1.20\) Å and \(1.55\) Å and, if Figure 21-1 (or anything similar) applies, we should not expect significant \(\ce{C-C}\) bonding at internuclear distances greater than \(2\) Å.
It is important to recognize that bonding occurs only if the electrons are paired (i.e., have opposite spins). The upper dashed curve of Figure 21-1 shows how the energy changes as two hydrogen atoms will parallel spins approach one another. That there is no net bonding can be understood by the Pauli principle (Section 6-1), which tells us that two electrons cannot be in the same orbital if they are unpaired.
Contributors and Attributions
John D. Robert and Marjorie C. Caserio (1977) Basic Principles of Organic Chemistry, second edition. W. A. Benjamin, Inc. , Menlo Park, CA. ISBN 0-8053-8329-8. This content is copyrighted under the following conditions, "You are granted permission for individual, educational, research and non-commercial reproduction, distribution, display and performance of this work in any format."


