6.3: Bond Formation Using Atomic Orbitals
- Page ID
- 22183
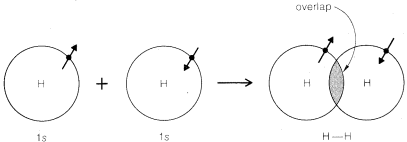
In writing the conventional Lewis structures for molecules, we assume that a covalent chemical bond between two atoms involves sharing a pair of elections, one from each atom. Figure 6-5 shows how atomic orbitals can be considered to be used in bond formation. Here, we postulate that a single bond is formed by the pulling together of two atomic nuclei by attractive forces exerted by the nuclei for the two paired electrons in overlapping atomic orbitals.
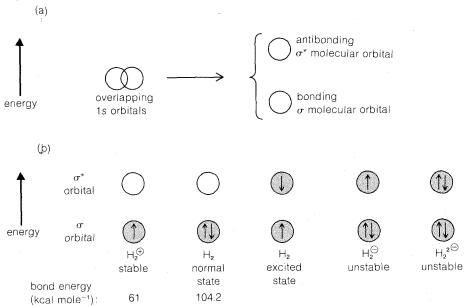
Because two atomic orbitals can hold a maximum of four electrons, it is reasonable to ask why it is that two rather than one, three, or four electrons normally are involved in a bond. The answer is that two overlapping atomic
orbitals can be considered to combine to give one low-energy bonding molecular orbital and one high-energy antibonding molecular orbital (see the top part of Figure 6-6(a)).\(^2\) Orbitals that overlap as shown in Figure 6-6(a) are said to overlap in the sigma manner,\(^3\) and the bonding orbital is called a sigma orbital (\(\sigma\)); the antibonding orbital is called a \(\sigma^*\) orbital (read "sigma star"). Two paired electrons suffice to fill the \(\sigma\) orbital. Any additional electrons must go into the high-energy \(\sigma^*\) orbital and contribute not to bonding but to repulsion between the atoms.
The hydrogen molecule-ion, \(H_2^\oplus\), can be regarded as having one electron in a \(\sigma\) orbital. It has been studied in the vapor state by spectroscopic means and found to have a dissociation energy to \(H^\oplus\) and \(H \cdot\) of \(61 \: \text{kcal mol}^{-1}\) compared to the \(104.2 \: \text{kcal mol}^{-1}\) bond energy for \(H_2\). Several possible combinations of two hydrogen orbitals and from one to four electrons are shown in Figure 6-6(b).
\(^2\)More about the difference between bonding and antibonding orbitals is given in Section 21-2. For now we will say that the property of orbitals that leads to bonding or antibonding is a property analogous to phase. An in-phase combination of two orbitals is bonding, and an out-of-phase combination is antibonding.
\(^3\)The designation sigma (\(\sigma\)) denotes that orbital overlap and electron density are greatest along the internuclear axis.
Contributors and Attributions
John D. Robert and Marjorie C. Caserio (1977) Basic Principles of Organic Chemistry, second edition. W. A. Benjamin, Inc. , Menlo Park, CA. ISBN 0-8053-8329-8. This content is copyrighted under the following conditions, "You are granted permission for individual, educational, research and non-commercial reproduction, distribution, display and performance of this work in any format."


