5.2: Configurational Isomers
- Page ID
- 22176
Geometric Isomerism
We have defined isomers in a very general way as nonidentical molecules that possess the same number and kind of atoms. However, there are several ways in which isomers can be nonidentical. Among the alkenes, 1- and 2-butene are position isomers, because in these compounds the double bond has a different position in the carbon chain:
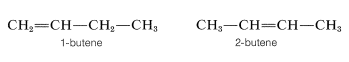
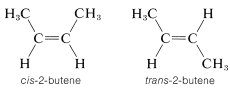
Most, but not all alkenes, have stereoisomers that are not identical because of different spatial arrangements of the component atoms. Thus there are two stereoisomers of 2-butene that differ in the geometric arrangement of the groups attached to the double bond. In one isomer, both methyl groups are on the same side of the double bond (cis-2-butene) and in the other, the methyl groups are on opposite sides of the double bond (trans-2-butene):
It should be clear to you that there will be no cis-trans isomers of alkenes in which one end of the double bond carries identical groups. Thus we don not expect there to be cis-trans isomers of 1-butene or 2-methylpropene, and
indeed none are known:

You may wish to verify this by making ball-and-stick models of these substances.
Ring formation also confers rigidity on molecular structure such that rotation about the ring bonds is prevented. As a result, stereoisomerism of the cis-trans type is possible. For example, 1,2-dimethylcyclopropane exists in two forms that differ in the arrangement of the two methyl groups with
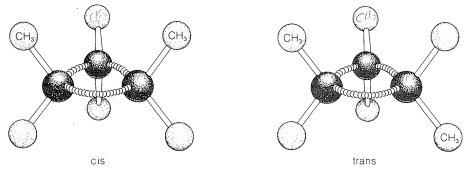
respect to the ring. In the cis isomer, the methyl groups both are situated above (or below) the plane of the ring and in the trans isomer they are situated one above and one below, as shown in Figure 5-2. Interconversion of these isomers does not occur without breaking one or more chemical bonds.
Stereoisomers that do not interconvert rapidly under normal conditions, and therefore are stable enough to be separated, specifically are called configurational isomers. Thus cis- and trans-2-butene are configurational isomers, as are cis- and trans-1,2-dimethylcyclopropane. The terms cis-trans isomerism or geometric isomerism commonly are used to describe configurational isomerism in compounds with double bonds and rings. When referring to the configuration of a particular isomer, we mean to specify its geometry. For instance, the isomer of 1,2-dichloroethene shown below has the trans configuration; the isomer of 1,3-dichlorocyclobutane has the cis configuration:
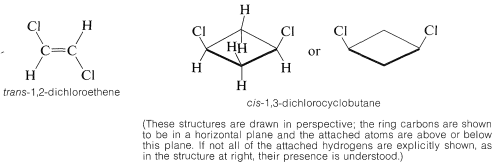
Cis-trans isomerism is encountered very frequently. By one convention, the configuration of a complex alkene is taken to correspond to the configuration of the longest continuous chain as it passes through the double bond. Thus the following compound is trans-4-ethyl-3-methyl-3-heptene, despite the fact that two identical groups are cis with respect to each other, because the longest continuous chain is trans as it passes through the double bond:
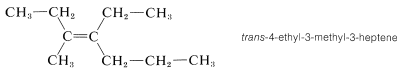
Notice that cis-trans isomerism is not possible at a carbon-carbon triple bond, as for 2-butyne, because the bonding arrangement at the triply bonded carbons is linear:

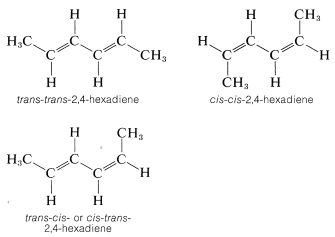
Many compounds have more than one double bond and each may have the potential for the cis or trans arrangement. For example, 2,4-hexadiene has three different configurations, which are designated as trans-trans, cis-cis, and trans-cis. Because the two ends of this molecule are identically substituted, the trans-cis becomes identical with cis-trans:
Chirality
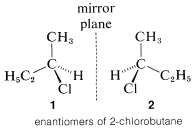
The most important type of stereoisomerism is that which arises when molecules possess two structures that are not identical and also are mirror images of one another. This is not a difficult or unfamiliar concept. Many things around us, such as our hands, and pairs of shoes, are not identical and also are mirror images of one another. In the same way, nonidentical molecules exist in which the only distinction between them is that one is the mirror image of the other. A common statement is that such isomers are mirror images of one another, but these images are not "superimposable." A simple example of this type of stereoisomerism is 2-chlorobutane,  , which can exist in two spatial configurations, \(1\) and \(2\), that correspond to reflections of each other. These isomers are specifically called enantiomers.
, which can exist in two spatial configurations, \(1\) and \(2\), that correspond to reflections of each other. These isomers are specifically called enantiomers.
Compounds that lack reflection symmetry - meaning that they are not identical with their mirror images - are said to be chiral (pronounced "ki-rall", rhymes with spiral). This term is derived from the Greek word \(\chi \epsilon \iota \rho =\) hand; and "handedness" or chirality is a property of dissymmetric molecules such that two configurational isomers are possible that are nonidentical mirror images. Compounds that possess reflection symmetry - meaning that they are identical with their mirror images - are said to be achiral. Enantiomers are not possible for achiral compounds. An enantiomeric pair is a pair of substances whose molecules are nonidentical mirror images.
The pressing question at this point is how can we tell whether a substances will be chiral or achiral. The most common origin of chirality in molecules, and the one originally recognized by van't Hoff and Le Bel, is the presence of one or more atoms, usually carbon atoms, each of which forms coplanar bonds to four different atoms or groups. This is the case for 2-chlorobutane, because the second tetrahedral carbon along the chain is bonded to four different groups: hydrogen, chlorine, methyl, and ethyl. Therefore there is a pair of enantiomers, \(1\) and \(2\). Another example is 2-bromo-2-chloro-1,1,1-trifluoroethane, which is a widely used inhalation anaesthetic. The four different groups in this case are hydrogen, chlorine, bromine, and trifluoromethyl; the pair of enantiomers is shown in Structures \(3\) and \(4\):

The atom that carries the four different substituents in \(1\) and \(2\), or \(3\) and \(4\), is called a chiral atoms or chiral center. The latter is the more general term because, as we shall see later (Section 13-5A), dissymmetry in molecules need not be centered at an atom.\(^1\)
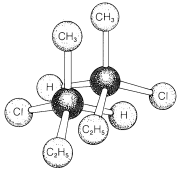
In evaluating a chemical structure for chirality, you should look for carbons carrying four different attached groups. There may be more than one chiral carbon, and you should be alert to the fact that structural differences in the attached groups do not necessarily show up at the first, or even the second, position along a chain. As an example, consider the chirality of 1,1,3-trimethylcyclohexane,

Carbons \(C2\), \(C4\), \(C5\), and \(C6\) are clearly achiral because each is connected to two identical groups, which for these atoms are hydrogens. The same is true for \(C1\) because it is connected to two \(CH_3\) groups. You might conclude that \(C3\) also is an achiral position because it is connected to two \(CH_2\) groups. But this would be wrong. If you look farther, you will see that the groups attached to \(C3\) actually are different and are \(H\), \(CH_3\), \(-CH_2CH_2CH_2-\), and \(-CH_2C \left( CH_3 \right)_2\). Therefore 1,1,3-trimethylcyclohexane has a chiral center at \(C3\). In contrast, the 1,1,4-isomer has no chiral centers because the groups attached to the ring at \(C4\) are identical:
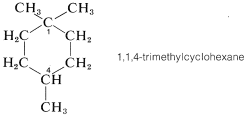
Several other terms that we shall use frequently in addition to chirality are racemic mixture, resolution, and racemization. A mixture of equal amounts of both enantiomers is a racemic mixture; separation of a racemic mixture into its component enantiomers is a resolution, and the conversion of either enantiomer into equal parts of both is called racemization.
Optical Activity
Until recently, the phenomenon of chirality has been better known as optical isomerism, and configurational isomers that are enantiomers were referred to as optical antipodes. The reasons for this are mainly historical. It was discovered early in the nineteenth century that many compounds, whether solid, liquid, or gas, have the property of rotating the plane of polarization of polarized light and can be said to be "optically active." A satisfactory explanation of the origin of optical activity came much later and developed in its modern form from the classic researches of Louis Pasteur, and from the concept of the three-dimensional carbon atoms expressed independently by J. H. van't Hoff and J. A. Le Bel.\(^2\)
Pasteur's contribution to stereochemistry came as a result of his studies of the shapes of crystals of tartaric acid, \(\ce{HO_2C-CHOH-CHOH-CO_2H}\), and its salts. Tartaric acid, a by-product of wine production, was known to be optically active, and Pasteur showed that it, and nineteen different salts of it, all formed crystals that were not identical with their mirror images. A different substance known as "racemic acid," for which we can write the same condensed formula, \(\ce{HO_2C-CHOH-CHOH-CO_2H}\), was known to be optically inactive, and Pasteur expected that when he crystallized this acid or its salts he would obtain crystals that would be identical with their mirror images. However, crystallization of the sodium ammonium salt of racemic acid from water at temperatures below \(28^\text{o}\) gave crystals of two different shapes and these shapes were mirror images of one another. Pasteur carefully picked apart the two kinds of crystals and showed that one of them was identical with the corresponding salt of tartaric acid, except that it rotated the plane of polarization of polarized light in the opposite direction. This separation of racemic acid into two optically active forms now is called a "resolution of racemic acid."
On the basis of his discoveries, Pasteur postulated that "optical isomerism" had to be related to the molecular dissymmetry of substances such that nonidentical mirror-image forms could exist. However, it remained for van' t Hoff and Le Bel to provide, almost simultaneously, a satisfactory explanation at the molecular level. In his first published work on tetrahedral carbon van't Hoff said "...it appears more and more that the present constitutional formulae are incapable of explaining certain cases of isomerism; the reason for this is perhaps the fact that we need a more definite statement about the actual positions of the atoms."\(^3\) He goes on to discuss the consequences of the tetrahedral arrangements of atoms about carbon, explicitly in connection with optical isomerism and geometric, or cis-trans, isomerism.
It is not easy for the chemist of today to appreciate fully the contributions of these early chemists because we have long accepted the tetrahedral carbon as an experimentally established fact. At the time the concept was enunciated, however, even the existence of atoms and molecules was questioned openly by many scientists, and to ascribe "shapes" to what in the first place seemed like metaphysical conceptions was too much for many to accept.
Properties of Enantiomers
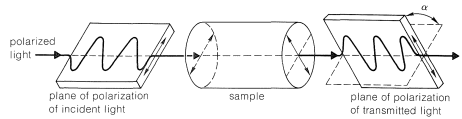
Optical activity is an experimentally useful property and usually is measured as the angle of rotation (\(\alpha\)) of the plane of polarization of polarized light passing through solutions of the substances under investigation (Figure 5-4). Where measurable optical activity is present, it is found that one enantiomer rotates the plane of polarization in one direction, whereas the other causes the plane to rotate equally but in the opposite direction. With reference to the plane of incident light, the enantiomer that rotates the plane to the right is called dextrorotatory and is symbolized by either d or (\(+\)); the enantiomer that rotates the plane to the left is levorotatory, symbolized by l or (\(-\)). A racemic mixture then can be designated as dl or (\(\pm\)), and will have no net optical rotation. It is very important to know that d, l, (\(+\)), or (\(-\)) do not designate configurations. Thus, although (\(+\))-2-butanol actually has configuration \(5\) and (\(-\))-2-butanol has configuration \(6\), there is no simple way to predict that a particular sign of rotation will be associated with a particular configuration. Methods used in assigning the true configurations to enantiomers will be discussed later.
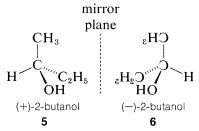
A very important point to keep in mind about any pair of enantiomers is that they will have identical chemical and physical properties, except for the signs of their optical rotations, with one important proviso: All of the properties to be compared must be determined using achiral reagents in a solvent made up of achiral molecules or, in short, in an achiral environment. Thus the melting and boiling points (but not the optical rotations) of \(5\) and \(6\) will be identical in an achiral environment. How a chiral environment or chiral reagents influence the properties of substances such as \(5\) and \(6\) will be considered in Chapter 19.
\(^1\)In the older literature, chiral centers often are called asymmetric centers and you may be confused by the difference between asymmetric and dissymmetric. Both asymmetric and dissymmetric molecules (or objects) are chiral. An asymmetric object has no symmetry at all and looks different from all angles of view. Formulas \(3\) and \(4\) represent asymmetric molecules. A dissymmetric molecule is chiral, but looks the same from more than one angle of view. A helical spring is dissymmetric - it looks the same from each end. We will encounter dissymmetric molecules later.
\(^2\)The tetrahedral carbon was first proposed by E. Paterno in 1869 (see Section1-1E), but he apparently did not recognize its implications for chirality. These implications were recognized first by van't Hoff and Le Bel, with van't Hoff proceeding on the basis of bonds to carbon being directed to the corners of a regular tetrahedron. Le Bel was opposed to such a rigid formulation of the bonds to carbon.
\(^3\)An interesting account and references to van't Hoff's early work can be found in "The Reception of J. H. van't Hoff's Theory of the Asymmetric Carbon" by H. A. M. Snelders, J. Chem. Educ. 51, 2 (1974). A century has passed since van't Hoff first published his theory, which he did before he obtained his doctoral degree from the University of Utrecht. van't Hoff was the first recipient of the Nobel Prize in chemistry (1901) for his later work in thermodynamics and chemical kinetics.
Contributors and Attributions
John D. Robert and Marjorie C. Caserio (1977) Basic Principles of Organic Chemistry, second edition. W. A. Benjamin, Inc. , Menlo Park, CA. ISBN 0-8053-8329-8. This content is copyrighted under the following conditions, "You are granted permission for individual, educational, research and non-commercial reproduction, distribution, display and performance of this work in any format."


