14.7: Phenols
- Page ID
- 16047
- To describe the structure and uses of some phenols
Compounds in which an OH group is attached directly to an aromatic ring are designated ArOH and called phenols. Phenols differ from alcohols in that they are slightly acidic in water. They react with aqueous sodium hydroxide (NaOH) to form salts.
\[\ce{ArOH (aq) + NaOH (aq) \rightarrow ArONa (aq) + H_2O} \nonumber \]
The parent compound, C6H5OH, is itself called phenol. (An old name, emphasizing its slight acidity, was carbolic acid.) Phenol is a white crystalline compound that has a distinctive (“hospital smell”) odor.
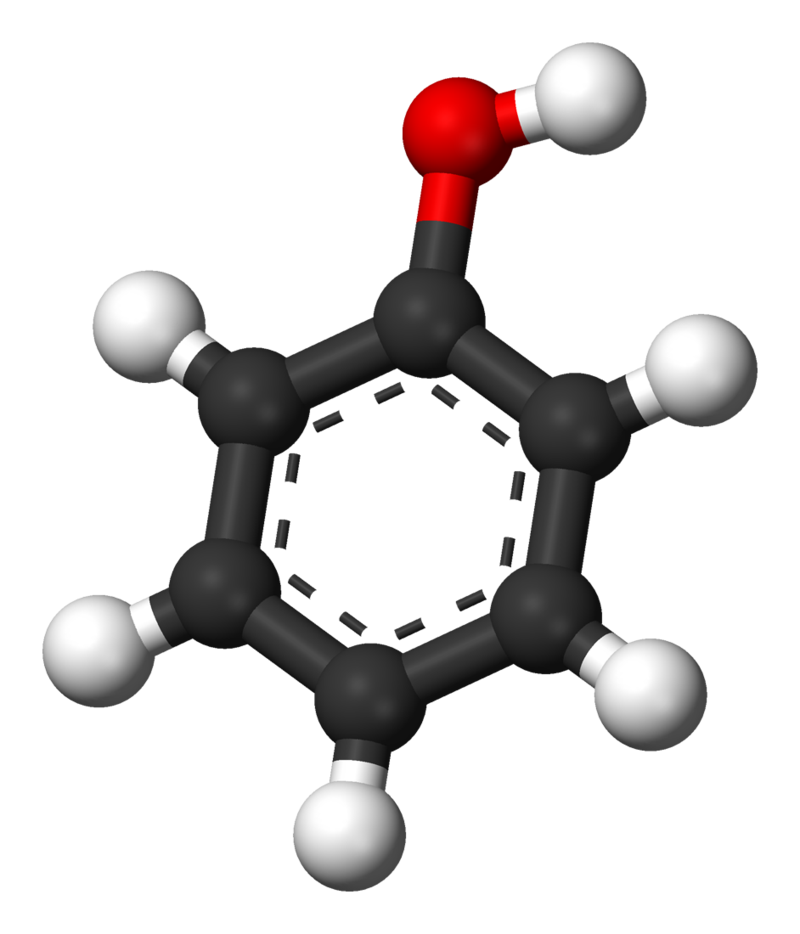

Phenols are widely used as antiseptics (substances that kill microorganisms on living tissue) and as disinfectants (substances intended to kill microorganisms on inanimate objects such as furniture or floors). The first widely used antiseptic was phenol. Joseph Lister used it for antiseptic surgery in 1867. Phenol is toxic to humans, however, and can cause severe burns when applied to the skin. In the bloodstream, it is a systemic poison—that is, one that is carried to and affects all parts of the body. Its severe side effects led to searches for safer antiseptics, a number of which have been found.
An operation in 1753, painted by Gaspare Traversi, of a surgery before antiseptics were used.
One safer phenolic antiseptic is 4-hexylresorcinol (4-hexyl-1,3-dihydroxybenzene; resorcinol is the common name for 1,3-dihydroxybenzene, and 4-hexylresorcinol has a hexyl group on the fourth carbon atom of the resorcinol ring). It is much more powerful than phenol as a germicide and has fewer undesirable side effects. Indeed, it is safe enough to be used as the active ingredient in some mouthwashes and throat lozenges.
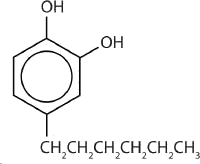
The compound 4-hexylresorcinol is mild enough to be used as the active ingredient in antiseptic preparations for use on the skin.
Summary
Phenols are compounds in which an OH group is attached directly to an aromatic ring. Many phenols are used as antiseptics.


