13.9: Freezing Point Depression and Boiling Point Elevation
- Page ID
- 47559
- Explain what the term "colligative" means, and list the colligative properties.
- Indicate what happens to the boiling point and the freezing point of a solvent when a solute is added to it.
- Calculate boiling point elevations and freezing point depressions for a solution.
People who live in colder climates have seen trucks put salt on the roads when snow or ice is forecast. Why is this done? As a result of the information you explore in this section, you will understand why these events occur. You will also learn to calculate exactly how much of an effect a specific solute can have on the boiling point or freezing point of a solution.
The example given in the introduction is an example of a colligative property. Colligative properties are properties that differ based on the concentration of solute in a solvent, but not on the type of solute. What this means for the example above is that people in colder climates do not necessarily need salt to get the same effect on the roads—any solute will work. However, the higher the concentration of solute, the more these properties will change.
Boiling Point Elevation
Water boils at \(100^\text{o} \text{C}\) at \(1 \: \text{atm}\) of pressure, but a solution of saltwater does not . When table salt is added to water, the resulting solution has a higher boiling point than the water did by itself. The ions form an attraction with the solvent particles that prevents the water molecules from going into the gas phase. Therefore, the saltwater solution will not boil at \(100^\text{o} \text{C}\). In order for the saltwater solution to boil, the temperature must be raised about \(100^\text{o} \text{C}\). This is true for any solute added to a solvent; the boiling point will be higher than the boiling point of the pure solvent (without the solute). In other words, when anything is dissolved in water, the solution will boil at a higher temperature than pure water would.
The boiling point elevation due to the presence of a solute is also a colligative property. That is, the amount of change in the boiling point is related to the number of particles of solute in a solution and is not related to the chemical composition of the solute. A \(0.20 \: \text{m}\) solution of table salt and a \(0.20 \: \text{m}\) solution of hydrochloric acid would have the same effect on the boiling point.
Freezing Point Depression
The effect of adding a solute to a solvent has the opposite effect on the freezing point of a solution as it does on the boiling point. A solution will have a lower freezing point than a pure solvent. The freezing point is the temperature at which the liquid changes to a solid. At a given temperature, if a substance is added to a solvent (such as water), the solute-solvent interactions prevent the solvent from going into the solid phase. The solute-solvent interactions require the temperature to decrease further in order to solidify the solution. A common example is found when salt is used on icy roadways. Salt is put on roads so that the water on the roads will not freeze at the normal \(0^\text{o} \text{C}\) but at a lower temperature, as low as \(-9^\text{o} \text{C}\). The de-icing of planes is another common example of freezing point depression in action. A number of solutions are used, but commonly a solution such as ethylene glycol, or a less toxic monopropylene glycol, is used to de-ice an aircraft. The aircrafts are sprayed with the solution when the temperature is predicted to drop below the freezing point. The freezing point depression is the difference in the freezing points of the solution from the pure solvent. This is true for any solute added to a solvent; the freezing point of the solution will be lower than the freezing point of the pure solvent (without the solute). Thus, when anything is dissolved in water, the solution will freeze at a lower temperature than pure water would.
The freezing point depression due to the presence of a solute is also a colligative property. That is, the amount of change in the freezing point is related to the number of particles of solute in a solution and is not related to the chemical composition of the solute. A \(0.20 \: \text{m}\) solution of table salt and a \(0.20 \: \text{m}\) solution of hydrochloric acid would have the same effect on the freezing point.
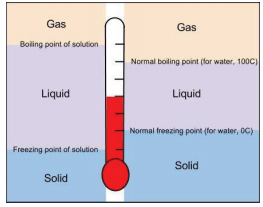
Comparing the Freezing and Boiling Point of Solutions
Recall that covalent and ionic compounds do not dissolve in the same way. Ionic compounds break up into cations and anions when they dissolve. Covalent compounds typically do not break up. For example a sugar/water solution stays as sugar and water, with the sugar molecules staying as molecules. Remember that colligative properties are due to the number of solute particles in the solution. Adding 10 molecules of sugar to a solvent will produce 10 solute particles in the solution. When the solute is ionic, such as \(\ce{NaCl}\) however, adding 10 formulas of solute to the solution will produce 20 ions (solute particles) in the solution. Therefore, adding enough \(\ce{NaCl}\) solute to a solvent to produce a \(0.20 \: \text{m}\) solution will have twice the effect of adding enough sugar to a solvent to produce a \(0.20 \: \text{m}\) solution. Colligative properties depend on the number of solute particles in the solution.
"\(i\)" is the number of particles that the solute will dissociate into upon mixing with the solvent. For example, sodium chloride, \(\ce{NaCl}\), will dissociate into two ions so for \(\ce{NaCl}\), \(i = 2\); for lithium nitrate, \(\ce{LiNO_3}\), \(i = 2\); and for calcium chloride, \(\ce{CaCl_2}\), \(i = 3\). For covalent compounds, \(i\) is always equal to 1.
By knowing the molality of a solution and the number of particles a compound will dissolve to form, it is possible to predict which solution in a group will have the lowest freezing point. To compare the boiling or freezing points of solutions, follow these general steps:
- Label each solute as ionic or covalent.
- If the solute is ionic, determine the number of ions in the formula. Be careful to look for polyatomic ions.
- Multiply the original molality (\(\text{m}\)) of the solution by the number of particles formed when the solution dissolves. This will give you the total concentration of particles dissolved.
- Compare these values. The higher total concentration will result in a higher boiling point and a lower freezing point.
Rank the following solutions in water in order of increasing (lowest to highest) freezing point:
- \(0.1 \: \text{m} \: \ce{NaCl}\)
- \(0.1 \: \text{m} \: \ce{C_6H_{12}O_6}\)
- \(0.1 \: \text{m} \: \ce{CaI_2}\)
Solution
To compare freezing points, we need to know the total concentration of all particles when the solute has been dissolved.
- \(0.1 \: \text{m} \: \ce{NaCl}\): This compound is ionic (metal with nonmetal), and will dissolve into 2 parts. The total final concentration is: \(\left( 0.1 \: \text{m} \right) \left( 2 \right) = 0.2 \: \text{m}\)
- \(0.1 \: \text{m} \: \ce{C_6H_{12}O_6}\): This compound is covalent (nonmetal with nonmetal), and will stay as 1 part. The total final concentration is: \(\left( 0.1 \: \text{m} \right) \left(1 \right) = 0.1 \: \text{m}\)
- \(0.1 \: \text{m} \: \ce{CaI_2}\): This compound is ionic (metal with nonmetal), and will dissolve into 3 parts. The total final concentration is: \(\left( 0.1 \: \text{m} \right) \left( 3 \right) = 0.3 \: \text{m}\)
Remember, the greater the concentration of particles, the lower the freezing point will be. \(0.1 \: \text{m} \: \ce{CaI_2}\) will have the lowest freezing point, followed by \(0.1 \: \text{m} \: \ce{NaCl}\), and the highest of the three solutions will be \(0.1 \: \text{m} \: \ce{C_6H_{12}O_6}\), but all three of them will have a lower freezing point than pure water.
The boiling point of a solution is higher than the boiling point of a pure solvent, and the freezing point of a solution is lower than the freezing point of a pure solvent. However, the amount to which the boiling point increases or the freezing point decreases depends on the amount of solute that is added to the solvent. A mathematical equation is used to calculate the boiling point elevation or the freezing point depression.
The boiling point elevation is the amount that the boiling point temperature increases compared to the original solvent. For example, the boiling point of pure water at \(1.0 \: \text{atm}\) is \(100^\text{o} \text{C}\) while the boiling point of a \(2\%\) saltwater solution is about \(102^\text{o} \text{C}\). Therefore, the boiling point elevation would be \(2^\text{o} \text{C}\). The freezing point depression is the amount that the freezing temperature decreases.
Both the boiling point elevation and the freezing point depression are related to the molality of the solution. Looking at the formula for the boiling point elevation and freezing point depression, we see similarities between the two. The equation used to calculate the increase in the boiling point is:
\[\Delta T_b = k_b \cdot \text{m} \cdot i \label{BP} \]
Where:
- \(\Delta T_b =\) the amount the boiling point increases.
- \(k_b =\) the boiling point elevation constant which depends on the solvent (for water, this number is \(0.515^\text{o} \text{C/m}\)).
- \(\text{m} =\) the molality of the solution.
- \(i =\) the number of particles formed when that compound dissolves (for covalent compounds, this number is always 1).
The following equation is used to calculate the decrease in the freezing point:
\[\Delta T_f = k_f \cdot \text{m} \cdot i \label{FP} \]
Where:
- \(\Delta T_f =\) the amount the freezing temperature decreases.
- \(k_f =\) the freezing point depression constant which depends on the solvent (for water, this number is \(1.86^\text{o} \text{C/m}\)).
- \(\text{m} =\) the molality of the solution.
- \(i =\) the number of particles formed when that compound dissolves (for covalent compounds, this number is always 1).
Antifreeze is used in automobile radiators to keep the coolant from freezing. In geographical areas where winter temperatures go below the freezing point of water, using pure water as the coolant could allow the water to freeze. Since water expands when it freezes, freezing coolant could crack engine blocks, radiators, and coolant lines. The main component in antifreeze is ethylene glycol, \(\ce{C_2H_4(OH)_2}\). What is the concentration of ethylene glycol in a solution of water, in molality, if the freezing point dropped by \(2.64^\text{o} \text{C}\)? The freezing point constant, \(k_f\), for water is \(1.86^\text{o} \text{C/m}\).
Solution
Use the equation for freezing point depression of solution (Equation \(\ref{FP}\)):
\[\Delta T_f = k_f \cdot \text{m} \cdot i \nonumber \]
Substituting in the appropriate values we get:
\[2.64^\text{o} \text{C} = \left( 1.86^\text{o} \text{C/m} \right) \left( \text{m} \right) \left( 1 \right) \nonumber \]
Solve for \(\text{m}\) by dividing both sides by \(1.86^\text{o} \text{C/m}\).
\[\text{m} = 1.42 \nonumber \]
A solution of \(10.0 \: \text{g}\) of sodium chloride is added to \(100.0 \: \text{g}\) of water in an attempt to elevate the boiling point. What is the boiling point of the solution? \(k_b\) for water is \(0.52^\text{o} \text{C/m}\).
Solution
Use the equation for boiling point elevation of solution (Equation \(\ref{BP}\)):
\[\Delta T_b = k_b \cdot \text{m} \cdot i \nonumber \]
We need to be able to substitute each variable into this equation.
- \(k_b = 0.52^\text{o} \text{C/m}\)
- \(\text{m}\): We must solve for this using stoichiometry. Given: \(10.0 \: \text{g} \: \ce{NaCl}\) and \(100.0 \: \text{g} \: \ce{H_2O}\) Find: \(\text{mol} \: \ce{NaCl}/\text{kg} \: \ce{H_2O}\). Ratios: molar mass of \(\ce{NaCl}\), \(1000 \: \text{g} = 1 \: \text{kg}\)
\[\dfrac{10.0 \: \cancel{\text{g} \: \ce{NaCl}}}{100.0 \: \cancel{\text{g} \: \ce{H_2O}}} \cdot \dfrac{1 \: \text{mol} \: \ce{NaCl}}{58.45 \: \cancel{\text{g} \: \ce{NaCl}}} \cdot \dfrac{1000 \: \cancel{\text{g} \: \ce{H_2O}}}{1 \: \text{kg} \: \ce{H_2O}} = 1.71 \: \text{m} \nonumber \]
- For \(\ce{NaCl}\), \(i = 2\)
Substitute these values into the equation \(\Delta T_b = k_b \cdot \text{m} \cdot i\). We get:
\[\Delta T_b = \left( 0.52 \dfrac{^\text{o} \text{C}}{\cancel{\text{m}}} \right) \left( 1.71 \: \cancel{\text{m}} \right) \left( 2 \right) = 1.78^\text{o} \text{C} \nonumber \]
Water normally boils at \(100^\text{o} \text{C}\), but our calculation shows that the boiling point increased by \(1.78^\text{o} \text{C}\). Our new boiling point is \(101.78^\text{o} \text{C}\).
Note: Since sea water contains roughly 28.0 g of NaCl per liter, this saltwater solution is approximately four times more concentrated than sea water (all for a 2° C rise of boiling temperature).
Summary
- Colligative properties are properties that are due only to the number of particles in solution, and are not related to the chemical properties of the solute.
- Boiling points of solutions are higher than the boiling points of the pure solvents.
- Freezing points of solutions are lower than the freezing points of the pure solvents.
- Ionic compounds split into ions when they dissolve, forming more particles. Covalent compounds stay as complete molecules when they dissolve.
Vocabulary
- Colligative property - A property that is due only to the number of particles in solution, and not the type of the solute.
- Boiling point elevation - The amount that the boiling point of a solution increases from the boiling point of the pure solvent.
- Freezing point depression - The amount that the freezing point of a solution decreases from the freezing point of the pure solvent.

