8.5: Stoichiometry
- Page ID
- 47499
- Explain the meaning of the term "stoichiometry".
- Determine the relative amounts of each substance in chemical equations.
You have learned that chemical equations provide us with information about the types of particles that react to form products. Chemical equations also provide us with the relative number of particles and moles that react to form products. In this section you will explore the quantitative relationships that exist between the quantities of reactants and products in a balanced equation. This is known as stoichiometry.
Stoichiometry, by definition, is the calculation of the quantities of reactants or products in a chemical reaction using the relationships found in the balanced chemical equation. The word stoichiometry is actually Greek from two words: \(\sigma \tau \omicron \iota \kappa \eta \iota \omicron \nu \), which means "element", and \(\mu \epsilon \tau \rho \omicron \nu), which means "measure".
Interpreting Chemical Equations
The mole, as you remember, is a quantitative measure that is equivalent to Avogadro's number of particles. So how does this relate to the chemical equation? Look at the chemical equation below.
\[2 \ce{CuSO_4} + 4 \ce{KI} \rightarrow 2 \ce{CuI} + 2 \ce{K_2SO_4} + \ce{I_2} \nonumber \]
The coefficients used, as we have learned, tell us the relative amounts of each substance in the equation. So for every 2 units of copper (II) sulfate (\(\ce{CuSO_4}\)) we have, we need to have 4 units of potassium iodide (\(\ce{KI}\)). For every two dozen copper (II) sulfates, we need 4 dozen potassium iodides. Because the unit "mole" is also a counting unit, we can interpret this equation in terms of moles, as well: For every two moles of copper (II) sulfate, we need 4 moles potassium iodide.
The production of ammonia \(\left( \ce{NH_3} \right)\) from nitrogen and hydrogen gases is an important industrial reaction called the Haber process, after German chemist Fritz Haber.
\[\ce{N_2} \left( g \right) + 3 \ce{H_2} \left( g \right) \rightarrow 2 \ce{NH_3} \left( g \right) \nonumber \]
The balanced equation can be analyzed in several ways, as shown in the figure below.
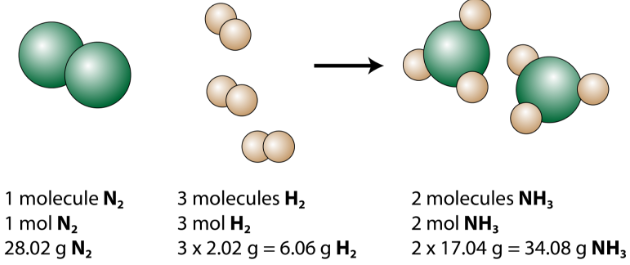
We see that 1 molecule of nitrogen reacts with 3 molecules of hydrogen to form 2 molecules of ammonia. This is the smallest possible relative amount of the reactants and products. To consider larger relative amounts, each coefficient can be multiplied by the same number. For example, 10 molecules of nitrogen would react with 30 molecules of hydrogen to produce 20 molecules of ammonia.
The most useful quantity for counting particles is the mole. So if each coefficient is multiplied by a mole, the balanced chemical equation tells us that 1 mole of nitrogen reacts with 3 moles of hydrogen to produce 2 moles of ammonia. This is the conventional way to interpret any balanced chemical equation.
Finally, if each mole quantity is converted to grams by using the molar mass, we can see that the law of conservation of mass is followed. \(1 \: \ce{mol}\) of nitrogen has a mass of \(28.02 \: \text{g}\), while \(3 \: \text{mol}\) of hydrogen has a mass of \(6.06 \: \text{g}\), and \(2 \: \text{mol}\) of ammonia has a mass of \(34.08 \: \text{g}\).
\[28.02 \: \text{g} \: \ce{N_2} + 6.06 \: \text{g} \: \ce{H_2} \rightarrow 34.08 \: \text{g} \: \ce{NH_3} \nonumber \]
Mass and the number of atoms must be conserved in any chemical reaction. The number of molecules is not necessarily conserved.
The equation for the combustion of ethane (\(\ce{C_2H_6}\)) is
\[2 \ce{C_2H_6} + 7 \ce{O_2} \rightarrow 4 \ce{CO_2} + 6 \ce{H_2O} \nonumber \]
- Indicate the number of formula units or molecules in the balanced equation.
- Indicate the number of moles present in the balanced equation.
Solution
- Two molecules of \(\ce{C_2H_6}\) plus seven molecules of \(\ce{O_2}\) yields four molecules of \(\ce{CO_2}\) plus six molecules of \(\ce{H_2O}\).
- Two moles of \(\ce{C_2H_6}\) plus seven moles of \(\ce{O_2}\) yields four moles of \(\ce{CO_2}\) plus six moles of \(\ce{H_2O}\).
For the following equation below, indicate the number of formula units or molecules, and the number of moles present in the balanced equation.
\[\ce{KBrO_3} + 6 \ce{KI} + 6 \ce{HBr} \rightarrow 7 \ce{KBr} + 3 \ce{H_2O} \nonumber \]
- Answer
-
One molecules of \(\ce{KBrO_3}\) plus six molecules of \(\ce{KI}\) plus six molecules of \(\ce{HBr}\) yields seven molecules of \(\ce{KBr}\) plus three molecules of \(\ce{I_2}\) and three molecules of \(\ce{H_2O}\). One mole of \(\ce{KBrO_3}\) plus six moles of \(\ce{KI}\) plus six moles of \(\ce{HBr}\) yields seven moles of \(\ce{KBr}\) plus three moles of \(\ce{I_2}\) plus three moles of \(\ce{H_2O}\).
Summary
- Stoichiometry is the calculation of the quantities of reactants or products in a chemical reaction using the relationships found in a balanced chemical equation.
- The coefficients in a balanced chemical equation represent the reacting ratios of the substances in the reaction.
- The coefficients of a balanced equation can be used to determine the ratio of moles of all substances in the reaction.
Vocabulary
- Stoichiometry - The calculation of quantitative relationships of the reactants and products in a balanced chemical equation.
- Formula unit - The empirical formula of an ionic compound.
- Mole ratio - The ratio of the moles of one reactant or product to the moles of another reactant or product according to the coefficients in the balanced chemical equation.

