6.9: Calculating Molecular Formulas for Compounds
- Page ID
- 47495
- Understand the difference between empirical formulas and molecular formulas.
- Determine molecular formula from percent composition and molar mass of a compound.
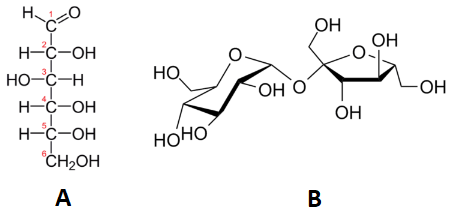
Below, we see two carbohydrates: glucose and sucrose. Sucrose is almost exactly twice the size of glucose, although their empirical formulas are very similar. Some people can distinguish them on the basis of taste, but it's not a good idea to go around tasting chemicals. The best way to tell glucose and sucrose apart is to determine the molar masses—this approach allows you to easily tell which compound is which.
Molecular Formulas
Molecular formulas give the kind and number of atoms of each element present in the molecular compound. In many cases, the molecular formula is the same as the empirical formula. The chemical formula will always be some integer multiple (\(n\)) of the empirical formula (i.e. integer multiples of the subscripts of the empirical formula).
\[\text{ Molecular Formula} = n (\text{Empirical formula}) \nonumber \]
therefore
\[ n = \dfrac{\text{Molecular Formula}}{\text{Empirical Formula}} \nonumber \]
The integer multiple, n, can also be obtained by dividing the molar mass, \(MM\), of the compound by the empirical formula mass, \(EFM\) (the molar mass represented by the empirical formula).
\[ n = \dfrac{MM ( molar mass)}{EFM (empirical formula molar mass)} \nonumber \]
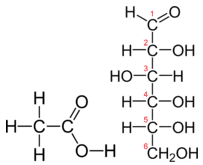
Table \(\PageIndex{1}\) shows the comparison between the empirical and molecular formula of methane, acetic acid, and glucose, and the different values of n. The molecular formula of methane is \(\ce{CH_4}\) and because it contains only one carbon atom, that is also its empirical formula. Sometimes, however, the molecular formula is a simple whole number multiple of the empirical formula. Acetic acid is an organic acid that is the main component of vinegar. Its molecular formula is \(\ce{C_2H_4O_2}\). Glucose is a simple sugar that cells use as a primary source of energy. Its molecular formula is \(\ce{C_6H_{12}O_6}\). The structures of both molecules are shown in Figure \(\PageIndex{2}\). They are very different compounds, yet both have the same empirical formula of \(\ce{CH_2O}\).
| Name of Compound | Molecular Formula | Empirical Formula | n |
|---|---|---|---|
| Methane | \(\ce{CH_4}\) | \(\ce{CH_4}\) | 1 |
| Acetic acid | \(\ce{C_2H_4O_2}\) | \(\ce{CH_2O}\) | 2 |
| Glucose | \(\ce{C_6H_{12}O_6}\) | \(\ce{CH_2O}\) | 6 |
Empirical formulas can be determined from the percent composition of a compound as discussed in section 6.8. In order to determine its molecular formula, it is necessary to know the molar mass of the compound. Chemists use an instrument called a mass spectrometer to determine the molar mass of compounds. In order to go from the empirical formula to the molecular formula, follow these steps:
- Calculate the empirical formula molar mass (EFM).
- Divide the molar mass of the compound by the empirical formula molar mass. The result should be a whole number or very close to a whole number.
- Multiply all the subscripts in the empirical formula by the whole number found in step 2. The result is the molecular formula.
The empirical formula of a compound of boron and hydrogen is \(\ce{BH_3}\). Its molar mass is \(27.7 \: \text{g/mol}\). Determine the molecular formula of the compound.
Solution
| Steps for Problem Solving | Determine the molecular formula of \(\ce{BH_3}\). |
|---|---|
| Identify the "given" information and what the problem is asking you to "find." |
Given: Empirical formula \(= \ce{BH_3}\) Molar mass \(= 27.7 \: \text{g/mol}\) Find: Molecular formula \(= ?\) |
| Calculate the empirical formula mass (EFM). | \[\text{Empirical formula molar mass (EFM)} = 13.84 \: \text{g/mol} \nonumber \] |
| Divide the molar mass of the compound by the empirical formula mass. The result should be a whole number or very close to a whole number. |
\[\dfrac{\text{molar mass}}{\text{EFM}} = \dfrac{27.7 g/mol}{13.84 g/mol} = 2 \nonumber \] |
| Multiply all the subscripts in the empirical formula by the whole number found in step 2. The result is the molecular formula. | \[\ce{BH_3} \times 2 = \ce{B_2H_6} \nonumber \] |
| Write the molecular formula. | The molecular formula of the compound is \(\ce{B_2H_6}\). |
| Think about your result. | The molar mass of the molecular formula matches the molar mass of the compound. |
Vitamin C (ascorbic acid) contains 40.92 % C, 4.58 % H, and 54.50 % O, by mass. The experimentally determined molecular mass is 176 amu. What are the empirical and chemical formulas for ascorbic acid?
- Answer Empirical Formula
- C3H4O3
- Answer Molecular Formula
- C6H8O6
Summary
- A procedure is described that allows the calculation of the exact molecular formula for a compound.

