10.3: Lewis Structures of Ionic Compounds- Electrons Transferred
- Page ID
- 47526
- State the octet rule.
- Define ionic bond.
- Draw Lewis structures for ionic compounds.
In Section 4.7, we demonstrated that ions are formed by losing electrons to make cations, or by gaining electrons to form anions. The astute reader may have noticed something: many of the ions that form have eight electrons in their valence shell. Either atoms gain enough electrons to have eight electrons in the valence shell and become the appropriately charged anion, or they lose the electrons in their original valence shell; the lower shell, now the valence shell, has eight electrons in it, so the atom becomes positively charged. For whatever reason, having eight electrons in a valence shell is a particularly energetically stable arrangement of electrons. The octet rule explains the favorable trend of atoms having eight electrons in their valence shell. When atoms form compounds, the octet rule is not always satisfied for all atoms at all times, but it is a very good rule of thumb for understanding the kinds of bonding arrangements that atoms can make.
It is not impossible to violate the octet rule. Consider sodium: in its elemental form, it has one valence electron and is stable. It is rather reactive, however, and does not require a lot of energy to remove that electron to make the Na+ ion. We could remove another electron by adding even more energy to the ion, to make the Na2+ ion. However, that requires much more energy than is normally available in chemical reactions, so sodium stops at a 1+ charge after losing a single electron. It turns out that the Na+ ion has a complete octet in its new valence shell, the n = 2 shell, which satisfies the octet rule. The octet rule is a result of trends in energies and is useful in explaining why atoms form the ions that they do.
Now consider an Na atom in the presence of a Cl atom. The two atoms have these Lewis electron dot diagrams and electron configurations:
\[\mathbf{Na\, \cdot }\; \; \; \; \; \; \; \; \; \; \mathbf{\cdot }\mathbf{\ddot{\underset{.\: .}Cl}}\mathbf{\: :} \nonumber \]
\[\left [ Ne \right ]3s^{1}\; \; \; \; \left [ Ne \right ]3s^{2}3p^{5} \nonumber \]
For the Na atom to obtain an octet, it must lose an electron; for the Cl atom to gain an octet, it must gain an electron. An electron transfers from the Na atom to the Cl atom:
\[\mathbf{Na\, \cdot }\curvearrowright \mathbf{\cdot }\mathbf{\ddot{\underset{.\: .}Cl}}\mathbf{\: :} \nonumber \]
resulting in two ions—the Na+ ion and the Cl− ion:
\[\mathbf{Na}^{+}\; \; \; \; \; \; \; \; \mathbf{:}\mathbf{\ddot{\underset{.\: .}Cl}}\mathbf{\: :}^{-} \nonumber \]
\[\left [ Ne \right ]\; \; \; \; \; \left [ Ne \right ]3s^{2}3p^{6} \nonumber \]
Both species now have complete octets, and the electron shells are energetically stable. From basic physics, we know that opposite charges attract. This is what happens to the Na+ and Cl− ions:
\[\mathbf{Na}^{+}\; + \; \mathbf{:}\mathbf{\ddot{\underset{.\: .}Cl}}\mathbf{\: :}^{-}\rightarrow Na^{+}Cl^{-}\; \; or\; \; NaCl \nonumber \]
where we have written the final formula (the formula for sodium chloride) as per the convention for ionic compounds, without listing the charges explicitly. The attraction between oppositely charged ions is called an ionic bond, and it is one of the main types of chemical bonds in chemistry. Ionic bonds are caused by electrons transferring from one atom to another.
In electron transfer, the number of electrons lost must equal the number of electrons gained. We saw this in the formation of NaCl. A similar process occurs between Mg atoms and O atoms, except in this case two electrons are transferred:
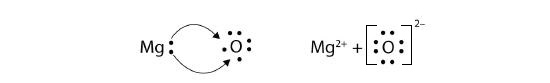
The two ions each have octets as their valence shell, and the two oppositely charged particles attract, making an ionic bond:
\[\mathbf{Mg\,}^{2+}\; + \; \left[\mathbf{:}\mathbf{\ddot{\underset{.\: .}O}}\mathbf{\: :}\right]^{2-}\; \; \; \; \; Mg^{2+}O^{2-}\; or\; MgO \nonumber \]
Remember, in the final formula for the ionic compound, we do not write the charges on the ions.
What about when an Na atom interacts with an O atom? The O atom needs two electrons to complete its valence octet, but the Na atom supplies only one electron:
\[\mathbf{Na\, \cdot }\curvearrowright \mathbf{\cdot }\mathbf{\ddot{\underset{.}O}}\mathbf{\: :} \nonumber \]
The O atom still does not have an octet of electrons. What we need is a second Na atom to donate a second electron to the O atom:
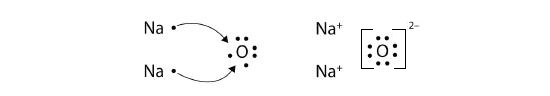
These three ions attract each other to give an overall neutral-charged ionic compound, which we write as Na2O. The need for the number of electrons lost being equal to the number of electrons gained explains why ionic compounds have the ratio of cations to anions that they do. This is required by the law of conservation of matter as well.
With arrows, illustrate the transfer of electrons to form calcium chloride from \(Ca\) atoms and \(Cl\) atoms.
Solution
A \(Ca\) atom has two valence electrons, while a \(Cl\) atom has seven electrons. A \(Cl\) atom needs only one more to complete its octet, while \(Ca\) atoms have two electrons to lose. Thus we need two \(Cl\) atoms to accept the two electrons from one \(Ca\) atom. The transfer process looks as follows:
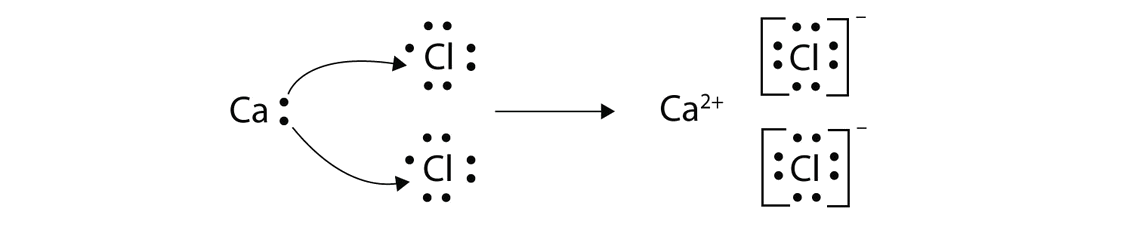
The oppositely charged ions attract each other to make CaCl2.
With arrows, illustrate the transfer of electrons to form potassium sulfide from \(K\) atoms and \(S\) atoms.
- Answer
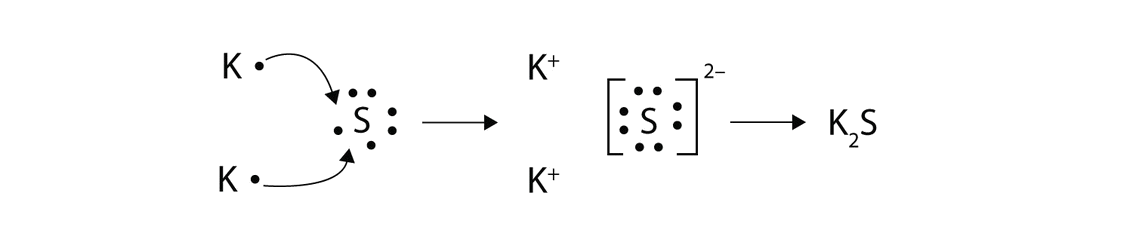
Summary
- The tendency to form species that have eight electrons in the valence shell is called the octet rule.
- The attraction of oppositely charged ions caused by electron transfer is called an ionic bond.
- The strength of ionic bonding depends on the magnitude of the charges and the sizes of the ions.

