3.7: Electron Arrangement- The Quantum Model
- Page ID
- 153790
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Represent the organization of electrons by an electron configuration based on the quantum mechanical model of an atom.
Quantum mechanics is the study of the motion of objects that are atomic or subatomic in size and thus demonstrate wave-particle duality. One of the fundamental (and hardest to understand) principles of quantum mechanics is that the electron is both a particles and a wave. In the everyday macroscopic world of things we can see, something cannot be both. But this duality can exist in the quantum world of the submicroscopic at the atomic scale.
At the heart of quantum mechanics is the idea that we cannot specify accurately the location of an electron. All we can say is that there is a probability that it exists within this certain volume of space. The scientist Erwin Schrödinger developed an equation that deals with these calculations, which we will not pursue at this time. Recall that in the Bohr model, the exact path of the electron was restricted to very well-defined circular orbits around the nucleus. An orbital is the quantum mechanical refinement of Bohr’s orbit. In contrast to his concept of a simple circular orbit with a fixed radius, orbitals are mathematically derived regions of space with different probabilities of having an electron.
Figure \(\PageIndex{1}\) The Erwin Schrödinger.
Building Atoms by Orbital Filling
In the quantum-mechanical model of an atom, electrons in the same atom that have the same principal quantum number (n) or principal energy level are said to occupy an electron shell of the atom. Orbitals define regions in space where you are likely to find electrons. As shown in Figure \(\PageIndex{2}\) s orbitals are spherical shaped, and p orbitals are dumb-bell shaped. Orbitals within a shell are divided into subshells (sublevels). There are two subshells in the second shell namely the 2s subshell (with one orbital) and the 2p subshell (with three orbitals), see Table \(\PageIndex{1}\). It should be noted that the diagrams in Figure \(\PageIndex{2}\) are estimates of the electron distribution in space, not surfaces electrons are fixed on.
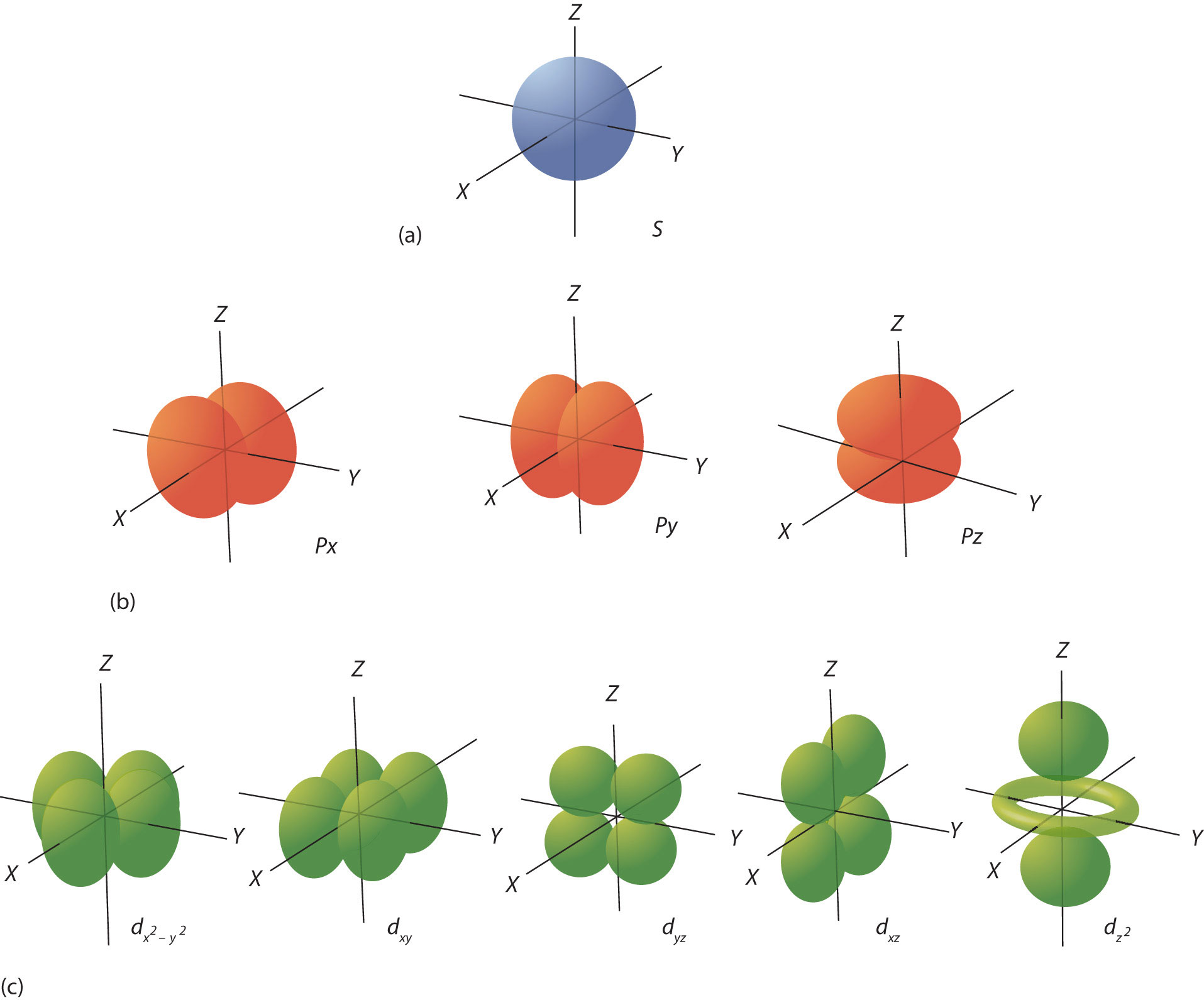
|
Principal Quantum Number \(\left( n \right)\) (Principal Shell) |
Sublevels (Subshell) |
Number of Orbitals per Sublevel |
Number of Electrons per Sublevel (Maximum of 2 electrons/orbital) |
|---|---|---|---|
| 1 | 1s |
1 (1s) |
2 |
| 2 | 2s |
1 (2s) |
2 |
| 2p |
3 (2px 2py 2pz) |
6 | |
| 3 | 3s |
1 (3s) |
2 |
| 3p |
3 (3px 3py 3pz) |
6 | |
| 3d |
5 (refer to Figure \(\PageIndex{2c}\)) |
10 |
In contrast to the shell model discussed in section 3.6, chemists more often use a more detailed electron configuration to represent the organization of electrons in shells and subshells in an atom. An atom's electron configuration includes the shell and subshell labels, with a right superscript giving the number of electrons in that subshell. The shells and subshells are listed in the order of filling. Electrons are typically organized around an atom by starting at the lowest possible quantum numbers first, which are the shells-subshells with lower energies.
For example, an H atom has a single electron in the 1s subshell. Its electron configuration is H: 1s1
He has two electrons in the 1s subshell. Its electron configuration is He: 1s2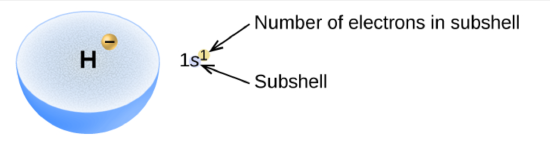
The three electrons for Li are arranged in the 1s subshell (two electrons) and the 2s subshell (one electron). The electron configuration of Li is
Li: 1s22s1
Figure \(\PageIndex{3}\) The diagram of an electron configuration of hydrogen right
specifies the subshell and superscript number of electrons.
| Element Name | Symbol | Atomic Number | Electron Configuration |
|---|---|---|---|
| Hydrogen | \(\ce{H}\) | 1 | \(1s^1\) |
| Helium | \(\ce{He}\) | 2 | \(1s^2\) |
| Lithium | \(\ce{Li}\) | 3 | \(1s^2 2s^1\) |
| Beryllium | \(\ce{Be}\) | 4 | \(1s^2 2s^2\) |
| Boron | \(\ce{B}\) | 5 | \(1s^2 2s^2 2p^1\) |
| Carbon | \(\ce{C}\) | 6 | \(1s^2 2s^2 2p^2\) |
| Nitrogen | \(\ce{N}\) | 7 | \(1s^2 2s^2 2p^3\) |
| Oxygen | \(\ce{O}\) | 8 | \(1s^2 2s^2 2p^4\) |
| Fluorine | \(\ce{F}\) | 9 | \(1s^2 2s^2 2p^5\) |
| Neon | \(\ce{Ne}\) | 10 | \(1s^2 2s^2 2p^6\) |
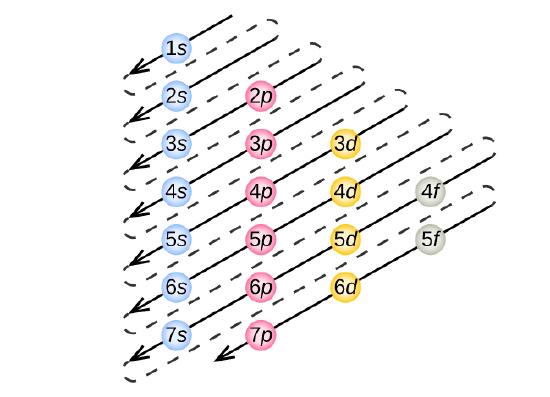
In order to create ground state electron configurations for any element, it is necessary to know the way in which the atomic sublevels are organized in order of increasing energy. Figure \(\PageIndex{4}\) shows the order of increasing energy of the sublevels.
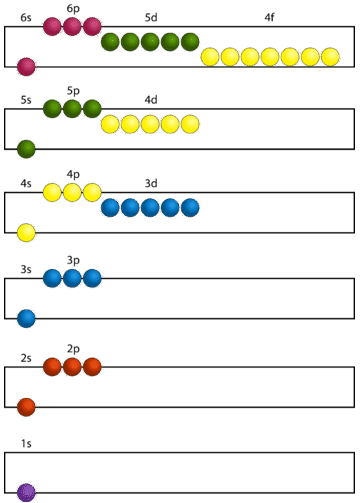
Figure \(\PageIndex{5}\) illustrates the traditional way to remember the filling order for atomic orbitals.
Nitrogen has 7 electrons. Write the electron configuration for nitrogen.
Solution:
Take a close look at Figure 9.6.5, and use it to figure out how many electrons go into each sublevel, and also the order in which the different sublevels get filled.
1. Begin by filling up the 1s sublevel. This gives 1s2. Now all of the orbitals in the red n = 1 block are filled.
- Since we used 2 electrons, there are 7 − 2 = 5 electrons left
2. Next, fill the 2s sublevel. This gives 1s22s2. Now all of the orbitals in the s sublevel of the orange n = 2 block are filled.
- Since we used another 2 electrons, there are 5 − 2 = 3 electrons left
3. Notice that we haven't filled the entire n = 2 block yet… there are still the p orbitals!
- The final 3 electrons go into the 2p sublevel. This gives 1s22s22p3
The overall electron configuration is: 1s22s22p3.
Potassium has 19 electrons. Write the electron configuration code for potassium.
Solution
This time, take a close look at Figure 9.6.5.
1. Begin by filling up the 1s sublevel. This gives 1s2. Now the n = 1 level is filled.
- Since we used 2 electrons, there are 19 − 2 = 17 electrons left
2. Next, fill the 2s sublevel. This gives 1s22s2
- Since we used another 2 electrons, there are 17 − 2 = 15 electrons left
3. Next, fill the 2p sublevel. This gives 1s22s22p6. Now the n = 2 level is filled.
- Since we used another 6 electrons, there are 15 − 6 = 9 electrons left
4. Next, fill the 3s sublevel. This gives 1s22s22p63s2
- Since we used another 2 electrons, there are 9 − 2 = 7 electrons left
5. Next, fill the 3p sublevel. This gives 1s22s22p63s23p6
- Since we used another 6 electrons, there are 7 − 6 = 1 electron left
Here's where we have to be careful – right after 3p6!!
- Remember, 4s comes before 3d!
6. The final electron goes into the 4s sublevel. This gives 1s22s22p63s23p64s1
The overall electron configuration is: 1s22s22p63s23p64s1.
What is the electron configuration for Mg and Na?
- Answer Mg
- Mg: 1s22s22p63s2
- Answer Na
- Na: 1s22s22p63s1
Summary
- Orbitals define regions in space where you are likely to find electrons. s orbitals are spherical shaped. p orbitals are dumb-bell shaped. The three possible p orbitals are always perpendicular to each other.
- Electron configuration notation simplifies the indication of where electrons are located in a specific atom. Superscripts are used to indicate the number of electrons in a given sublevel.
- Electrons are added to atomic orbitals in order from low energy to high energy.
Contributors and Attributions
Henry Agnew (UC Davis)
Paul Flowers (University of North Carolina - Pembroke), Klaus Theopold (University of Delaware) and Richard Langley (Stephen F. Austin State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at http://cnx.org/contents/85abf193-2bd...a7ac8df6@9.110).
- TextMap: Beginning Chemistry (Ball et al.)

