2.3: John Dalton and the Atomic Theory of Matter
- Page ID
- 152142
- Summarize Dalton's atomic theory.
- Explain the Law of multiple proportions.
While it must be assumed that many more scientists, philosophers, and others studied composition of matter after Democritus, a major leap forward in our understanding of the composition of matter took place in the 1800s with the work of the British scientist John Dalton. He started teaching school at age twelve, and was primarily known as a teacher. In his twenties, he moved to the growing city of Manchester, where he was able to pursue some scientific studies. His work in several areas of science brought him a number of honors. When he died, over 40,000 people in Manchester marched at his funeral.
Dalton's modern atomic theory, proposed around 1803, is a fundamental concept that states that all elements are composed of atoms. Previously, we defined an atom as the smallest part of an element that maintains the identity of that element. Individual atoms are extremely small; even the largest atom has an approximate diameter of only 5.4 × 10−10 m. At that size, it takes over 18 million of these atoms, lined up side by side, to equal the width of a human pinky finger (about 1 cm).

Dalton studied the weights of various elements and compounds. He noticed that matter always combined in fixed ratios based on weight, or volume in the case of gases. Chemical compounds always contain the same proportion of elements by mass, regardless of amount, which provided further support for Proust's law of definite proportions. Dalton also observed that there could be more than one combination of two elements.
From his experiments and observations, as well as the work from peers of his time, Dalton proposed his new theory of the atom. This later became known as Dalton's atomic theory. The general tenets of this theory were as follows:
- All matter is composed of extremely small particles called atoms.
- Atoms of a given element are identical in size, mass, and other properties (Figure \(\PageIndex{2}\) ). Atoms of different elements differ in size, mass, and other properties.

- Atoms cannot be subdivided, created, or destroyed.
- Atoms of different elements can combine in simple whole number ratios to form chemical compounds (Figure \(\PageIndex{3}\)).
- In chemical reactions, atoms are combined, separated, or rearranged.

Dalton's atomic theory has been largely accepted by the scientific community, with the exception of three changes. Present-day science acknowledges that:
(1) An atom can be further subdivided.
(2) All atoms of an element are not identical in mass.
(3) Using nuclear fission and fusion techniques, we can create or destroy atoms by changing them into other atoms.

In the following drawing, the green spheres represent atoms of a certain element. The purple spheres represent atoms of another element. If the spheres touch, they are part of a single unit of a compound. Does the following chemical change represented by these symbols violate any of the ideas of Dalton’s atomic theory? If so, which one?
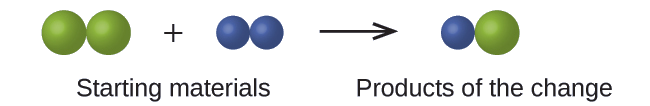
Solution
The starting materials consist of two green spheres and two purple spheres. The products consist of only one green sphere and one purple sphere. This violates Dalton’s postulate that atoms are neither created nor destroyed during a chemical change, but are merely redistributed. (In this case, atoms appear to have been destroyed.)
In the following drawing, the green spheres represent atoms of a certain element. The purple spheres represent atoms of another element. If the spheres touch, they are part of a single unit of a compound. Does the following chemical change represented by these symbols violate any of the ideas of Dalton’s atomic theory? If so, which one?

- Answer
-
The starting materials consist of four green spheres and two purple spheres. The products consist of four green spheres and two purple spheres. This does not violate any of Dalton’s postulates—atoms are neither created nor destroyed, but are redistributed in small, whole-number ratios.
Law of Multiple Proportions
Many combinations of elements can react to form more than one compound. In such cases, the masses of a particular element that combine with a fixed mass of a second element are demonstrable in ratios of small whole numbers. It's easy to say this, but please make sure that you understand how it works. Nitrogen forms a very large number of oxides, five of which are shown here.

- Line 1 shows the ratio of the relative weights of the two elements in each compound. These ratios were calculated by simply taking the molar mass of each element, and multiplying by the number of atoms of that element per mole of the compound. Thus for NO2, we have (1 × 14) : (2 × 16) = 14:32. (These numbers were not known in the early days of Chemistry because atomic weights [i.e., molar masses] of most elements were not reliably known.)
- The numbers in Line 2 are just the mass ratios of O:N, found by dividing the corresponding ratios in line 1. But someone who depends solely on experiment would work these out by finding the mass of O that combines with unit mass (1 g) of nitrogen.
- Line 3 is obtained by dividing the figures of the Line 2 by the smallest O:N ratio in Line 2 (which is the ratio for N2O). Note that just as the law of multiple proportions says, the weight of oxygen that combines with unit weight of nitrogen work out to small integers; there is a typo in Line 3—where there is a 3, there should be a 4.
- Of course, we just as easily could have illustrated the law by considering the mass of nitrogen that combines with one gram of oxygen; it works both ways!
The law of multiple proportions states that if two elements form more than one compound between them, the masses of one element combined with a fixed mass of the second element form in ratios of small integers.
Video \(\PageIndex{1}\) The law of multiple proportions
A sample of compound A (a clear, colorless gas) is analyzed and found to contain 4.27 g carbon and 5.69 g oxygen. A sample of compound B (also a clear, colorless gas) is analyzed and found to contain 5.19 g carbon and 13.84 g oxygen. Are these data an example of the law of definite proportions, the law of multiple proportions, or neither? What do these data tell you about substances A and B?
Solution
In compound A, the mass ratio of carbon to oxygen is:
\[\mathrm{\dfrac{1.33\: g\: O}{1\: g\: C}} \nonumber \]
In compound B, the mass ratio of carbon to oxygen is:
\[\mathrm{\dfrac{2.67\: g\: O}{1\: g\: C}} \nonumber \]
The ratio of these ratios is:
\[\mathrm{\dfrac{\dfrac{1.33\: g\: O}{1\: g\: C}}{\dfrac{2.67\: g\: O}{1\: g\: C}}=\dfrac{1}{2}} \nonumber \]
This supports the law of multiple proportions. This means that A and B are different compounds, with A having one-half as much carbon per amount of oxygen (or twice as much oxygen per amount of carbon) as B. A possible pair of compounds that would fit this relationship would be A = CO2 and B = CO.
A sample of compound X (a clear, colorless, combustible liquid with a noticeable odor) is analyzed and found to contain 14.13 g carbon and 2.96 g hydrogen. A sample of compound Y (a clear, colorless, combustible liquid with a noticeable odor that is slightly different from X’s odor) is analyzed and found to contain 19.91 g carbon and 3.34 g hydrogen. Are these data an example of the law of definite proportions, the law of multiple proportions, or neither? What do these data tell you about substances X and Y?
- Answer
-
In compound X, the mass ratio of carbon to hydrogen is \(\mathrm{\dfrac{14.13\: g\: C}{2.96\: g\: H}}\).
In compound Y, the mass ratio of carbon to hydrogen is \(\mathrm{\dfrac{19.91\: g\: C}{3.34\: g\: H}}\).
The ratio of these ratios is
\[\mathrm{\dfrac{\dfrac{14.13\: g\: C}{2.96\: g\: H}}{\dfrac{19.91\: g\: C}{3.34\: g\: H}}=\dfrac{4.77\: g\: C/g\: H}{5.96\: g\: C/g\: H}=0.800=\dfrac{4}{5}}. \nonumber \]
This small, whole-number ratio supports the law of multiple proportions. This means that X and Y are different compounds.
The evidence for atoms is so great that few doubt their existence. In fact, individual atoms are now routinely observed with state-of-the art technologies. Moreover, they can even be used for making pretty images or, as IBM research demonstrates in Video \(\PageIndex{1}\), control of individual atoms can be used to create animations.
Video\(\PageIndex{1}\): A Boy And His Atom: The World's Smallest Movie
A Boy and His Atom is a 2012 stop-motion animated short film released by IBM Research. The movie tells the story of a boy and a wayward atom who meet and become friends. It depicts a boy playing with an atom that takes various forms. It was made by moving carbon monoxide molecules viewed with a scanning tunneling microscope, a device that magnifies them 100 million times. These molecules were moved to create images, which were then saved as individual frames to make the film.
Summary
- Dalton's Atomic Theory is the first scientific theory to relate chemical changes to the structure, properties, and behavior of the atom. The general tenets of this theory were as follows:
- All matter is composed of extremely small particles called atoms.
- Atoms of a given element are identical in size, mass, and other properties. Atoms of different elements differ in size, mass, and other properties.
- Atoms cannot be subdivided, created, or destroyed.
- Atoms of different elements can combine in simple whole number ratios to form chemical compounds.
- The law of multiple proportions states that whenever the same two elements form more than one compound, the different masses of one element that combine with the same mass of the other element are in the ratio of small whole numbers.
Contributors and Attributions
Henry Agnew (UC Davis)
- TextMap: Chemistry - The Central Science (Brown et al.)
Paul Flowers (University of North Carolina - Pembroke), Klaus Theopold (University of Delaware) and Richard Langley (Stephen F. Austin State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at http://cnx.org/contents/85abf193-2bd...a7ac8df6@9.110).

