1.6: The Measurement of Matter
- Page ID
- 152314
- Express quantities properly, using a number and a unit.
- State the different measurement systems used in chemistry.
- Express a large number or a small number in scientific notation.
- Learn how to use SI prefixes.
- Perform unit conversions using conversion factors.
A coffee maker’s instructions tell you to fill the coffeepot with 4 cups of water and use 3 scoops of coffee. When you follow these instructions, you are measuring. When you visit a doctor’s office, a nurse checks your temperature, height, weight, and perhaps blood pressure (Figure \(\PageIndex{1}\)); the nurse is also measuring.
Chemists measure the properties of matter and express these measurements as quantities. A quantity is an amount of something, and consists of a number and a unit. The number tells us how many (or how much), and the unit tells us what the scale of measurement is. For example, when a distance is reported as “5 kilometers,” we know that the quantity has been expressed in units of kilometers and that the number of kilometers is 5. If you ask a friend how far he or she walks from home to school, and the friend answers “12” without specifying a unit, you do not know whether your friend walks 12 miles, 12 kilometers, 12 furlongs, or 12 yards...etc. Both a number and a unit must be included to express a quantity properly.
To understand chemistry, we need a clear understanding of the units chemists work with and the rules they follow for expressing numbers. The next two sections examine the rules for expressing numbers.
All measurements depend on the use of units that are well known and understood. The English system of measurement units (inches, feet, ounces, etc.) are not used in science because of the difficulty in converting from one unit to another. The metric system is used because all metric units are based on multiples of 10, making conversions very simple. The metric system was originally established in France in 1795. The International System of Units is a system of measurement based on the metric system. The acronym SI is commonly used to refer to this system and stands for the French term, Le Système International d'Unités. The SI was adopted by international agreement in 1960 and is composed of the seven base units shown in Table \(\PageIndex{1}\).
| Quantity | SI Base Unit | Symbol |
|---|---|---|
| Length | meter | \(\text{m}\) |
| Mass | kilogram | \(\text{kg}\) |
| Temperature | kelvin | \(\text{K}\) |
| Time | second | \(\text{s}\) |
| Amount of a Substance | mole | \(\text{mol}\) |
| Electric Current | ampere | \(\text{A}\) |
| Luminous Intensity | candela | \(\text{cd}\) |
The first units are frequently encountered in chemistry. All other measurement quantities, such as volume, force, and energy, can be derived from these seven base units.
Exponential Numbers: Powers of Ten
Chemists often work with numbers that are exceedingly large or small. For example, entering the mass in grams of a hydrogen atom into a calculator would require a display with at least 24 decimal places. A system called scientific notation avoids much of the tedium and awkwardness of manipulating numbers with large or small magnitudes. Furthermore, use of prefixes is another way to express measurements involving large and small numbers.
Scientific Notation
In scientific notation, numbers are expressed in the form
\[ N \times 10^n \nonumber \]
where N is greater than or equal to 1 and less than 10 (1 ≤ N < 10), and n is a positive or negative integer (100 = 1). The number 10 is called the base because it is this number that is raised to the power \(n\). Although a base number may have values other than 10, the base number in scientific notation is always 10.
A simple way to convert numbers to scientific notation is to move the decimal point as many places to the left or right as needed to give a number from 1 to 10 (N). The magnitude of n is then determined as follows:
- If the decimal point is moved to the left n places, n is positive.
- If the decimal point is moved to the right n places, n is negative.
Another way to remember this is to recognize that as the number N decreases in magnitude, the exponent increases and vice versa. The application of this rule is illustrated in Example \(\PageIndex{1}\).
Convert each number to scientific notation.
- 637.8
- 0.0479
- 12,378
- 0.00032
Solution
| Explanation | Answer | |
|---|---|---|
| a |
To convert 637.8 to a number from 1 to 10, we move the decimal point two places to the left: 637.8 Because the decimal point was moved two places to the left, n = 2. |
\(6.378 \times 10^2\) |
| b |
To convert 0.0479 to a number from 1 to 10, we move the decimal point two places to the right: 0.0479 Because the decimal point was moved two places to the right, n = −2. |
\(4.79 \times 10^{−2}\) |
| c | Because the decimal point was moved four places to the left, n = 4. | \(1.2378 \times 10^4\) |
| d | Because the decimal point was moved four places to the right, n = −4. | \(3.2 \times 10^{−4}\) |
Convert each ordinary number to scientific notation, or vice versa.
- 67,000,000,000
- 1,689
- 12.6
- Answer a
- 6.7 × 1010
- Answer b
- 1.689 × 103
- Answer c
- 1.26 × 101
Convert each ordinary number to scientific notation, or vice versa.
- 0.000006567
- 6.22 × 10−2
- 9.9 × 10−9
- Answer a
- 6.567 × 10−6
- Answer b
- 0.0622
- Answer c
- 0.0000000099
Metric Prefixes
Conversions between metric system units are straightforward because the system is based on powers of ten. For example, meters, centimeters, and millimeters are all metric units of length. There are 10 millimeters in 1 centimeter and 100 centimeters in 1 meter. Metric prefixes are used to distinguish between units of different size. These prefixes all derive from either Latin or Greek terms. For example, mega comes from the Greek word \(\mu \varepsilon \gamma \alpha \varsigma\), meaning "great". Table \(\PageIndex{2}\) lists the most common metric prefixes and their relationship to the central unit that has no prefix. Length is used as an example to demonstrate the relative size of each prefixed unit.
| Prefix | Unit Abbreviation | Meaning | Example |
|---|---|---|---|
| giga | \(\text{G}\) | 1,000,000,000 | 1 gigameter \(\left( \text{Gm} \right)=10^9 \: \text{m}\) |
| mega | \(\text{M}\) | 1,000,000 | 1 megameter \(\left( \text{Mm} \right)=10^6 \: \text{m}\) |
| kilo | \(\text{k}\) | 1,000 | 1 kilometer \(\left( \text{km} \right)=1,000 \: \text{m}\) |
| hecto | \(\text{h}\) | 100 | 1 hectometer \(\left( \text{hm} \right)=100 \: \text{m}\) |
| deka | \(\text{da}\) | 10 | 1 dekameter \(\left( \text{dam} \right)=10 \: \text{m}\) |
| 1 | 1 meter \(\left( \text{m} \right)\) | ||
| deci | \(\text{d}\) | 1/10 | 1 decimeter \(\left( \text{dm} \right)=0.1 \: \text{m}\) |
| centi | \(\text{c}\) | 1/100 | 1 centimeter \(\left( \text{cm} \right)=0.01 \: \text{m}\) |
| milli | \(\text{m}\) | 1/1,000 | 1 millimeter \(\left( \text{mm} \right)=0.001 \: \text{m}\) |
| micro | \(\mu\) | 1/1,000,000 | 1 micrometer \(\left( \mu \text{m} \right)=10^{-6} \: \text{m}\) |
| nano | \(\text{n}\) | 1/1,000,000,000 | 1 nanometer \(\left( \text{nm} \right)=10^{-9} \: \text{m}\) |
| pico | \(\text{p}\) | 1/1,000,000,000,000 | 1 picometer \(\left( \text{pm} \right)=10^{-12} \: \text{m}\) |
There are a couple of odd little practices with the use of metric abbreviations. Most abbreviations are lowercase. We use "\(\text{m}\)" for meter and not "\(\text{M}\)". However, when it comes to volume, the base unit "liter" is abbreviated as "\(\text{L}\)" and not "\(\text{l}\)". So, 3.5 milliliters is written as \(3.5 \: \text{mL}\).
As a practical matter, whenever possible, you should express the units in a small and manageable number. If you are measuring the weight of a material that weighs \(6.5 \: \text{kg}\), this is easier than saying it weighs \(6500 \: \text{g}\) or \(0.65 \: \text{dag}\). All three are correct, but the \(\text{kg}\) units in this case make for a small and easily managed number. However, if a specific problem needs grams instead of kilograms, go with the grams for consistency.
Give the abbreviation for each unit and define the abbreviation in terms of the base unit.
- kiloliter
- microsecond
- decimeter
- nanogram
Solutions
| Explanation | Answer | |
|---|---|---|
| a | The prefix kilo means “1,000 ×,” so 1 kL equals 1,000 L | kL |
| b | The prefix micro implies 1/1,000,000th of a unit, so 1 µs equals 0.000001 s. | µs |
| c | The prefix deci means 1/10th, so 1 dm equals 0.1 m. | dm |
| d | The prefix nano means 1/1000000000, so a nanogram is equal to 0.000000001 g | ng |
Give the abbreviation for each unit and define the abbreviation in terms of the base unit.
- kilometer
- milligram
- nanosecond
- centiliter
- Answer a:
- km
- Answer b:
- mg
- Answer c:
- ns
- Answer d:
- cL
Mass and Weight
Mass is a measure of the amount of matter that an object contains. The mass of an object is made in comparison to the standard mass of 1 kilogram. The kilogram was originally defined as the mass of \(1 \: \text{L}\) of liquid water at \(4^\text{o} \text{C}\) (volume of a liquid changes slightly with temperature). In the laboratory, mass is measured with a balance (see below), which must be calibrated with a standard mass so that its measurements are accurate.

Other common units of mass are the gram and the milligram. A gram is 1/1000th of a kilogram, meaning that there are \(1000 \: \text{g}\) in \(1 \: \text{kg}\). A milligram is 1/1000th of a gram, so there are \(1000 \: \text{mg}\) in \(1 \: \text{g}\).
Mass is often confused with the term weight. Weight is a measure of force that is equal to the gravitational pull on an object. The weight of an object is dependent on its location. On the moon, the force due to gravity is about one sixth that of the gravitational force on Earth. Therefore, a given object will weigh six times more on Earth than it does on the moon. Since mass is dependent only on the amount of matter present in an object, mass does not change with location. Weight measurements are often made with a spring scale, by reading the distance that a certain object pulls down and stretches a spring.
Length and Volume
Length is the measurement of the extent of something along its greatest dimension. The SI basic unit of length, or linear measure, is the meter \(\left( \text{m} \right)\). All measurements of length may be made in meters, though the prefixes listed in various tables will often be more convenient. The width of a room may be expressed as about 5 meters \(\left( \text{m} \right)\), whereas a large distance, such as the distance between New York City and Chicago, is better expressed as 1150 kilometers \(\left( \text{km} \right)\). Very small distances can be expressed in units such as the millimeter or the micrometer. The width of a typical human hair is about 10 micrometers \(\left( \mu \text{m} \right)\).

Volume is the amount of space occupied by a sample of matter. The volume of a regular object can be calculated by multiplying its length by its width and its height. Since each of those is a linear measurement, we say that units of volume are derived from units of length. The SI unit of volume is the cubic meter \(\left( \text{m}^3 \right)\), which is the volume occupied by a cube that measures \(1 \: \text{m}\) on each side. This very large volume is not very convenient for typical use in a chemistry laboratory. A liter \(\left( \text{L} \right)\) is the volume of a cube that measures \(10 \: \text{cm}\) \(\left( 1 \: \text{dm} \right)\) on each side. A liter is thus equal to both \(1000 \: \text{cm}^3\) \(\left( 10 \: \text{cm} \times 10 \: \text{cm} \times 10 \: \text{cm} \right)\) and to \(1 \: \text{dm}^3\).
1L = \(1000 \: \text{cm}^3\) \(\left( 10 \: \text{cm} \times 10 \: \text{cm} \times 10 \: \text{cm} \right)\) = \(1 \: \text{dm}^3\)
A smaller unit of volume that is commonly used is the milliliter (\(\text{mL}\)). A milliliter is the volume of a cube that measures \(1 \: \text{cm}\) on each side. Therefore, a milliliter is equal to a cubic centimeter \(\left( \text{cm}^3 \right)\).
1 mL \(\left( \text{cm}^3 \right)\)
There are \(1000 \: \text{mL}\) in \(1 \: \text{L}\), which is the same as saying that there are \(1000 \: \text{cm}^3\) in \(1 \: \text{dm}^3\).


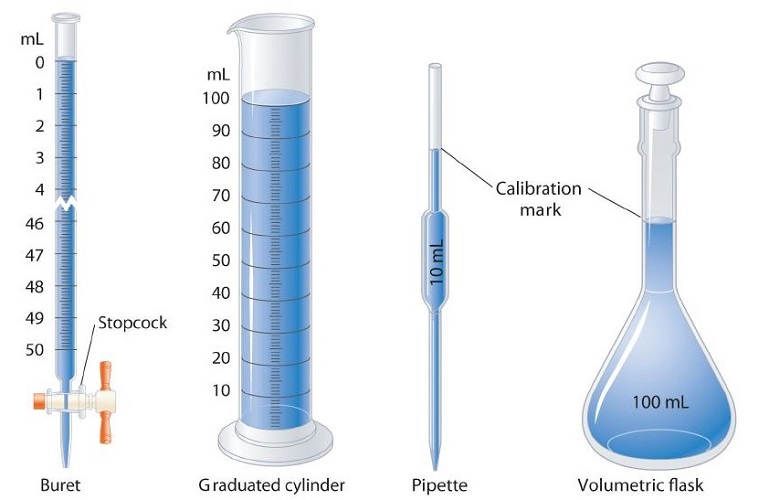
During your studies of chemistry (and physics also), you will note that mathematical equations are used in many different applications. Many of these equations have a number of different variables with which you will need to work. You should also note that these equations will often require you to use measurements with their units. Algebra skills become very important here!
Converting Between Units with Conversion Factors
A conversion factor is a factor used to convert one unit of measurement into another. A simple conversion factor can be used to convert meters into centimeters, or a more complex one can be used to convert miles per hour into meters per second. Since most calculations require measurements to be in certain units, you will find many uses for conversion factors. Always remember that a conversion factor has to represent a fact; this fact can either be simple or much more complex. For instance, you already know that 12 eggs equal one dozen. A more complex fact is that the speed of light is \(1.86 \times 10^5\) miles/sec. Either one of these can be used as a conversion factor, depending on what type of calculation you might be working with (Table \(\PageIndex{1}\)).
| English Units | Metric Units | Quantity |
|---|---|---|
| 1 ounce (oz) | 28.35 grams (g) | *mass |
| 1 fluid once (oz) | 2.96 mL | volume |
| 2.205 pounds (lb) | 1 kilogram (kg) | *mass |
| 1 inch (in) | 2.54 centimeters (cm) | length |
| 0.6214 miles (mi) | 1 kilometer (km) | length |
| 1 quarter (qt) | 0.95 liters (L) | volume |
*Pounds and ounces are technically units of force, not mass, but this fact is often ignored by the non-scientific community.
Of course, there are other ratios which are not listed in Table \(\PageIndex{1}\). They may include:
- Ratios embedded in the text of the problem (using words such as per or in each, or using symbols such as / or %).
- Conversions in the metric system, as covered earlier in this chapter.
- Common knowledge ratios (such as 60 seconds \(=\) 1 minute).
If you learned the SI units and prefixes described, then you know that 1 cm is 1/100th of a meter.
\[ 1\; \rm{cm} = \dfrac{1}{100} \; \rm{m} = 10^{-2}\rm{m} \nonumber \]
or
\[100\; \rm{cm} = 1\; \rm{m} \nonumber \]
Suppose we divide both sides of the equation by \(1 \text{m}\) (both the number and the unit):
\[\mathrm{\dfrac{100\:cm}{1\:m}=\dfrac{1\:m}{1\:m}} \nonumber \]
As long as we perform the same operation on both sides of the equals sign, the expression remains an equality. Look at the right side of the equation; it now has the same quantity in the numerator (the top) as it has in the denominator (the bottom). Any fraction that has the same quantity in the numerator and the denominator has a value of 1:
\[ \dfrac{ \text{100 cm}}{\text{1 m}} = \dfrac{ \text{1000 mm}}{\text{1 m}}= \dfrac{ 1\times 10^6 \mu \text{m}}{\text{1 m}}= 1 \nonumber \]
We know that 100 cm is 1 m, so we have the same quantity on the top and the bottom of our fraction, although it is expressed in different units.
Performing Dimensional Analysis
Dimensional analysis is amongst the most valuable tools used by physical scientists. Simply put, it is the conversion between an amount in one unit to the corresponding amount in a desired unit, using various conversion factors. This is valuable because certain measurements are more accurate or easier to find than others. The use of units in a calculation to ensure that we obtain the final proper units is called dimensional analysis.
Here is a simple example: How many centimeters are there in 3.55 m? Perhaps you can determine the answer in your head. If there are 100 cm in every meter, then 3.55 m equals 355 cm. To solve the problem more formally with a conversion factor, we first write the quantity we are given, 3.55 m. Then we multiply this quantity by a conversion factor, which is the same as multiplying it by 1. We can write 1 as \(\mathrm{\frac{100\:cm}{1\:m}}\) and multiply:
\[ 3.55 \; \rm{m} \times \dfrac{100 \; \rm{cm}}{1\; \rm{m}} \nonumber \]
The 3.55 m can be thought of as a fraction with a 1 in the denominator. Because m, the abbreviation for meters, occurs in both the numerator and the denominator of our expression, they cancel out:
\[\dfrac{3.55 \; \cancel{\rm{m}}}{ 1} \times \dfrac{100 \; \rm{cm}}{1 \; \cancel{\rm{m}}} \nonumber \]
The final step is to perform the calculation that remains once the units have been canceled:
\[ \dfrac{3.55}{1} \times \dfrac{100 \; \rm{cm}}{1} = 355 \; \rm{cm} \nonumber \]
In the final answer, we omit the 1 in the denominator. Thus, by a more formal procedure, we find that 3.55 m equals 355 cm. A generalized description of this process is as follows:
quantity (in old units) × conversion factor = quantity (in new units)
You may be wondering why we use a seemingly complicated procedure for a straightforward conversion. In later studies, the conversion problems you will encounter will not always be so simple. If you can master the technique of applying conversion factors, you will be able to solve a large variety of problems.
In the previous example, we used the fraction \(\frac{100 \; \rm{cm}}{1 \; \rm{m}}\) as a conversion factor. Does the conversion factor \(\frac{1 \; \rm m}{100 \; \rm{cm}}\) also equal 1? Yes, it does; it has the same quantity in the numerator as in the denominator (except that they are expressed in different units). Why did we not use that conversion factor? If we had used the second conversion factor, the original unit would not have canceled, and the result would have been meaningless. Here is what we would have gotten:
\[ 3.55 \; \rm{m} \times \dfrac{1\; \rm{m}}{100 \; \rm{cm}} = 0.0355 \dfrac{\rm{m}^2}{\rm{cm}} \nonumber \]
For the answer to be meaningful, we have to construct the conversion factor in a form that causes the original unit to cancel out. Figure \(\PageIndex{1}\) shows a concept map for constructing a proper conversion.
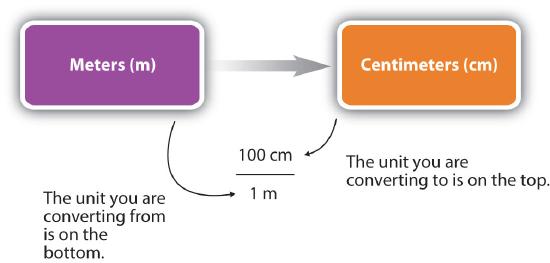
- Identify the "given" information in the problem. Look for a number with units to start this problem with.
- What is the problem asking you to "find"? In other words, what unit will your answer have?
- Use ratios and conversion factors to cancel out the units that aren't part of your answer, and leave you with units that are part of your answer.
- When your units cancel out correctly, you are ready to do the math. You are multiplying fractions, so you multiply the top numbers and divide by the bottom numbers in the fractions.
| Example \(\PageIndex{2}\) | Example \(\PageIndex{3}\) | |
|---|---|---|
| Steps for Problem Solving | The average volume of blood in an adult male is 4.7 L. What is this volume in gallons? | A hummingbird can flap its wings once in 18 ms. How many seconds are in 18 ms? |
| Identify the "given" information and what the problem is asking you to "find." | Given: 4.7 L Find: gal |
Given: 18 ms Find: s |
| List other known quantities. | \(1\, L = 3.785 gal \) | \(1 \,ms = 10^{-3} s \) |
| Prepare a concept map and use the proper conversion factor. | 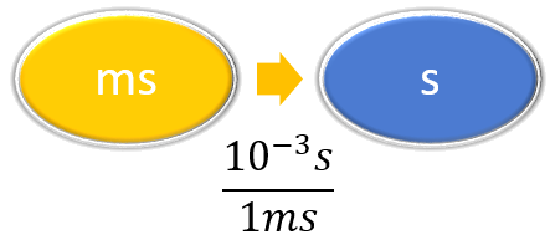 |
|
| Cancel units and calculate. | \( 4.7 \cancel{\rm{L}} \times \dfrac{1 \; \rm{gal}}{3.785\; \cancel{\rm{L}}} = 1.2\; \rm{gal}\) |
\( 18 \; \cancel{\rm{ms}} \times \dfrac{10^{-3}\; \rm{s}}{1 \; \cancel{\rm{ms}}} = 0.018\; \rm{s}\) or \( 18 \; \cancel{\rm{ms}} \times \dfrac{1\; \rm{s}}{1,000 \; \cancel{\rm{ms}}} = 0.018\; \rm{s}\) |
| Think about your result. | The amount in gal should be slightly less than 4 times smaller than the given amount in L. | The amount in s should be 1/1000 the given amount in ms. |
Perform each conversion.
- 101,000 ns to seconds
- 32.08 kg to grams
- 1.53 grams to cg
- Answer a:
- \(1.01000 x 10^{-4} s \)
- Answer b:
- \(3.208 x 10^{4} g \)
- Answer c:
- \(1.53 x 10^{2} g \)
Multiple Conversions
Sometimes you will have to perform more than one conversion to obtain the desired unit. For example, suppose you want to convert 54.7 km into millimeters. We will set up a series of conversion factors so that each conversion factor produces the next unit in the sequence. We first convert the given amount in km to the base unit, which is meters. We know that 1,000 m =1 km. Then we convert meters to mm, remembering that \(1\; \rm{mm}\) = \( 10^{-3}\; \rm{m}\).
Concept Map
Calculation
\[ \begin{align} 54.7 \; \cancel{\rm{km}} \times \dfrac{1,000 \; \cancel{\rm{m}}}{1\; \cancel{\rm{km}}} \times \dfrac{1\; \cancel{\rm{mm}}}{\cancel{10^{-3} \rm{m}}} & = 54,700,000 \; \rm{mm} \\ &= 5.47 \times 10^7\; \rm{mm} \end{align} \nonumber \]
In each step, the previous unit is canceled and the next unit in the sequence is produced; each successive unit cancels out, until only the unit needed in the answer is left.
Convert 58.2 ms to megaseconds in one multi-step calculation.
Solution
Steps for Problem Solving |
Unit Conversion |
|---|---|
| Identify the "given" information and what the problem is asking you to "find." |
Given: 58.2 ms Find: Ms |
| List other known quantities. |
\(1 ms = 10^{-3} s \) \(1 Ms = 10^6s \) |
| Prepare a concept map. |
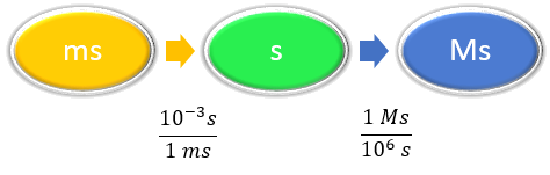
|
| Calculate. |
\[ \begin{align} 58.2 \; \cancel{\rm{ms}} \times \dfrac{10^{-3} \cancel{\rm{s}}}{1\; \cancel{\rm{ms}}} \times \dfrac{1\; \rm{Ms}}{1,000,000\; \cancel{ \rm{s}}} & =0.0000000582\; \rm{Ms} \nonumber\\ &= 5.82 \times 10^{-8}\; \rm{Ms}\nonumber \end{align}\nonumber \] Neither conversion factor affects the number of significant figures in the final answer. |
How many seconds are in a day?
Solution
Steps for Problem Solving |
Unit Conversion |
|---|---|
| Identify the "given" information and what the problem is asking you to "find." |
Given: 1 day Find: s |
| List other known quantities. |
1 day = 24 hours 1 hour = 60 minutes 1 minute = 60 seconds |
| Prepare a concept map. |
|
| Calculate. | \[1 \: \text{d} \times \frac{24 \: \text{hr}}{1 \: \text{d}}\times \frac{60 \: \text{min}}{1 \: \text{hr}} \times \frac{60 \: \text{s}}{1 \: \text{min}} = 86,400 \: \text{s} \nonumber \] |
Perform each conversion in one multistep calculation.
- 43.007 ng to kg
- 1005 in to ft
- 12 mi to km
- Answer a:
- \(4.3007 x 10^{-14} kg \)
- Answer b:
- 83.75 ft
- Answer c:
- 19 km
Summary
- Metric prefixes derive from Latin or Greek terms. The prefixes are used to make the units manageable.
- The SI system is based on multiples of ten. There are seven basic units in the SI system. Five of these units are commonly used in chemistry.
- Mass is a measure of the amount of matter that an object contains.
- Weight is a measure of force that is equal to the gravitational pull on an object.
- Mass is independent of location, while weight depends on location.
- Length is the measurement of the extent of something along its greatest dimension.
- Volume is the amount of space occupied by a sample of matter.
- Volume can be determined by knowing the length of each side of the item.
- Conversion factors are used to convert one unit of measurement into another.
- Dimensional analysis (unit conversions) involves the use of conversion factors that will cancel unwanted units and produce desired units.
Contributors and Attributions
Henry Agnew (UC Davis)
- Hayden Cox (Furman University)

