11.2: Half-Life
- Page ID
- 16074
- To define half-life.
- To determine the amount of radioactive substance remaining after a given number of half-lives.
Whether or not a given isotope is radioactive is a characteristic of that particular isotope. Some isotopes are stable indefinitely, while others are radioactive and decay through a characteristic form of emission. As time passes, less and less of the radioactive isotope will be present, and the level of radioactivity decreases. An interesting and useful aspect of radioactive decay is the half-life. The half-life of a radioactive isotope is the amount of time it takes for one-half of the radioactive isotope to decay. The half-life of a specific radioactive isotope is constant; it is unaffected by conditions and is independent of the initial amount of that isotope.
Consider the following example. Suppose we have 100.0 g of 3H (tritium, a radioactive isotope of hydrogen). It has a half-life of 12.3 y. After 12.3 y, half of the sample will have decayed to 3He by emitting a beta particle, so that only 50.0 g of the original 3H remains. After another 12.3 y—making a total of 24.6 y—another half of the remaining 3H will have decayed, leaving 25.0 g of 3H. After another 12.3 y—now a total of 36.9 y—another half of the remaining 3H will have decayed, leaving 12.5 g of 3H. This sequence of events is illustrated in Figure \(\PageIndex{1}\).

We can determine the amount of a radioactive isotope remaining after a given number half-lives by using the following expression:
\[\mathrm{amount\: remaining=initial\: amount\times \left ( \dfrac{1}{2} \right )^n} \label{Eq1} \]
where n is the number of half-lives. This expression works even if the number of half-lives is not a whole number.
The half-life of 20F is 11.0 s. If a sample initially contains 5.00 g of 20F, how much 20F remains after 44.0 s?
Solution
If we compare the time that has passed to the isotope’s half-life, we note that 44.0 s is exactly 4 half-lives, so we can use Equation \ref{E1} with \(n = 4\). Substituting and solving results in the following:
\[ \begin{align*} \mathrm{amount\: remaining} &=5.00\: g \times \left(\dfrac{1}{2}\right)^4 \\[4pt] &=5.00\: g \times \dfrac{1}{16} \\[4pt] &=0.313\: g \end{align*} \nonumber \]
Less than one-third of a gram of 20F remains.
The half-life of 44Ti is 60.0 y. A sample initially contains 0.600 g of 44Ti. How much 44Ti remains after 180.0 y?
- Answer
-
0.075 g.
Half-lives of isotopes range from fractions of a microsecond to billions of years. Table \(\PageIndex{1}\) lists the half-lives of some isotopes.
| Isotope | Half-Life |
|---|---|
| 3H | 12.3 y |
| 14C | 5,730 y |
| 40K | 1.26 × 109 y |
| 51Cr | 27.70 d |
| 90Sr | 29.1 y |
| 131I | 8.04 d |
| 222Rn | 3.823 d |
| 235U | 7.04 × 108 y |
| 238U | 4.47 × 109 y |
| 241Am | 432.7 y |
| 248Bk | 23.7 h |
| 260Sg | 4 ms |
The isotope \(\ce{I}\)-125 is used in certain laboratory procedures and has a half-life of 59.4 days. If the initial activity of a sample of \(\ce{I}\)-125 is \(32,000 \: \text{counts per minute (cpm)}\), how much activity will be present in 178.2 days?
Solution
We begin by determining how many half-lives are represented by 178.2 days:
\[\dfrac{178.2 \: \text{days}}{59.4 \: \text{days/half-life}} = 3 \: \text{half-lives} \nonumber \]
Then we simply count activity:
\[\begin{align} \text{initial activity} \: \left( t_0 \right) &= 32,000 \: \text{cpm} \nonumber\\ \text{after one half-life} \: &= 16,000 \: \text{cpm} \nonumber\\ \text{after two half-lives} \: &= 8,000 \: \text{cpm} \nonumber\\ \text{after three half-lives} &= 4,000 \: \text{cpm} \nonumber \end{align} \nonumber \]
Be sure to keep in mind that the initial count is at time zero \(\left( t_0 \right)\) and we subtract from that count at the first half-life. The second half-life has an activity of half the previous count (not the initial count).
Equation \(\ref{Eq1}\) can be used to calculate the amount of radioactivity remaining after a given time:
\[N_t = N_0 \times \left( 0.5 \right)^\text{number of half-lives} \nonumber \]
where \(N_t =\) activity at time \(t\) and \(N_0 =\) initial activity at time \(t = 0\).
If we have an initial activity of \(42,000 \: \text{cpm}\), what will the activity be after four half-lives?
\[\begin{align} N_t &= N_0 \left( 0.5 \right)^4 \nonumber \\ &= \left( 42,000 \right) \left( 0.5 \right) \left( 0.5 \right) \left( 0.5 \right) \left( 0.5 \right) \nonumber \\ &= 2625 \: \text{cpm} \nonumber \end{align} \nonumber \]
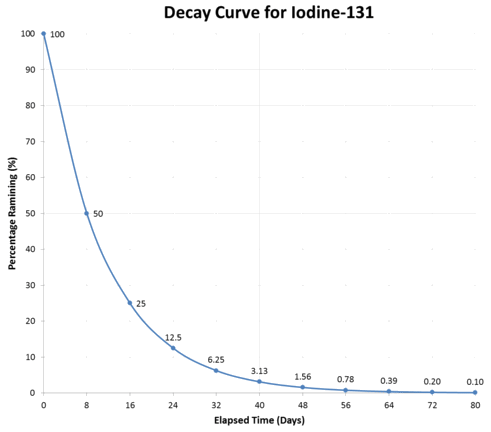
Typical radioactive decay curve.
The graph above illustrates a typical decay curve for \(\ce{I}-125\). The activity decreases by one-half during each succeeding half-life.
Exercise \(\PageIndex{2}\)
A sample of \(\ce{Ac}\)-225 originally contained 80 grams and after 50 days only 2.5 grams of the original \(\ce{Ac}\)-225 remain. What is the half life of \(\ce{Ac}\)-225?
- Answer
-
10 days
Many people think that the half-life of a radioactive element represents the amount of time an element is radioactive. In fact, it is the time required for half—not all—of the element to decay radioactively. Occasionally, however, the daughter element is also radioactive, so its radioactivity must also be considered.
The expected working life of an ionization-type smoke detector (described in the opening essay) is about 10 years. In that time, americium-241, which has a half-life of about 432 y, loses less than 4% of its radioactivity. A half-life of 432 y may seem long to us, but it is not very long as half-lives go. Uranium-238, the most common isotope of uranium, has a half-life of about 4.5 × 109 y, while thorium-232 has a half-life of 14 × 109 y.
On the other hand, some nuclei have extremely short half-lives, presenting challenges to the scientists who study them. The longest-lived isotope of lawrencium, 262Lr, has a half-life of 3.6 h, while the shortest-lived isotope of lawrencium, 252Lr, has a half-life of 0.36 s. As of this writing, the largest atom ever detected has atomic number 118, mass number 293, and a half-life of 120 ns. Can you imagine how quickly an experiment must be done to determine the properties of elements that exist for so short a time?
Key Takeaways
- Natural radioactive processes are characterized by a half-life, the time it takes for half of the material to decay radioactively.
- The amount of material left over after a certain number of half-lives can be easily calculated.


