17.12: Multi-Step Problems with Changes of State
- Page ID
- 53880
If you have a cube of ice, which process will take more energy—the melting of that ice cube or the conversion of the water to steam? The short answer is that more energy is needed to convert the water to steam. The long answer is really a series of questions: How do you get from one point to the other? What is the temperature of the ice? What is the mass of that ice cube? A long process is involved to take the material from the starting point to the end point.
Multi-Step Problems with Changes of State
Heating curves show the phase changes that a substance undergoes as heat is continuously absorbed.
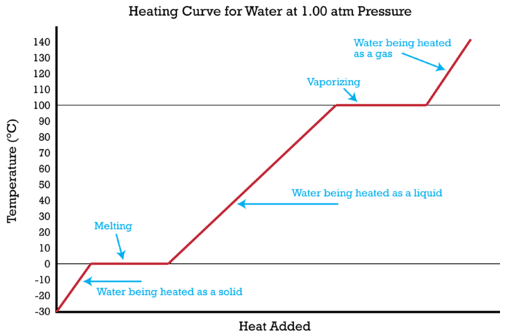
The specific heat of a substance allows us to calculate the heat absorbed or released as the temperature of the substance changes. It is possible to combine that type of problem with a change of state to solve a problem involving multiple steps. The figure above shows ice at \(-30^\text{o} \text{C}\) being converted in a five-step process to gaseous water (steam) at \(140^\text{o} \text{C}\). It is now possible to calculate the heat absorbed during that entire process. The process and the required calculations are summarized below.
1. Ice is heated from \(-30^\text{o} \text{C}\) to \(0^\text{o} \text{C}\). The heat absorbed is calculated by using the specific heat of ice and the equation \(\Delta H = c_p \times m \times \Delta T\).
2. Ice is melted at \(0^\text{o} \text{C}\). The heat absorbed is calculated by multiplying the moles of ice by the molar heat of fusion.
3. Water at \(0^\text{o} \text{C}\) is heated to \(100^\text{o} \text{C}\). The heat absorbed is calculated by using the specific heat of water and the equation \(\Delta H = c_p \times m \times \Delta T\).
4. Water is vaporized to steam at \(100^\text{o} \text{C}\). The heat absorbed is calculated by multiplying the moles of water by the molar heat of vaporization.
5. Steam is heated from \(100^\text{o} \text{C}\) to \(140^\text{o} \text{C}\). The heat absorbed is calculated by using the specific heat of steam and the equation \(\Delta H = c_p \times m \times \Delta T\).
Example \(\PageIndex{1}\)
Calculate the total amount of heat absorbed (in \(\text{kJ}\)) when \(2.00 \: \text{mol}\) of ice at \(-30^\text{o} \text{C}\) is converted to steam at \(140.0^\text{o} \text{C}\). The required specific heats can be found in the table in "Heat Capacity and Specific Heat".
Solution
Step 1: List the known quantities and plan the problem.
Known
- \(2.00 \: \text{mol}\) ice \(= 36.04 \: \text{g}\) ice
- \(c_p\) (ice) \(= 2.06 \: \text{J/g}^\text{o} \text{C}\)
- \(c_p\) (water) \(= 4.18 \: \text{J/g}^\text{o} \text{C}\)
- \(c_p\) (steam) \(= 1.87 \: \text{J/g}^\text{o} \text{C}\)
- \(\Delta H_\text{fus} = 6.01 \: \text{kJ/mol}\)
- \(\Delta H_\text{vap} = 40.7 \: \text{kJ/mol}\)
Unknown
Follow the steps previously described. Note that the mass of the water is needed for the calculations that involve the specific heat, while the moles of water is needed for the calculations that involve changes of state. All heat quantities must be in kilojoules so that they can be added together to get a total for the five-step process.
Step 2: Solve.
- \[\Delta H_1 = 2.06 \: \text{J/g}^\text{o} \text{C} \times 36.04 \: \text{g} \times 30^\text{o} \text{C} \times \frac{1 \: \text{kJ}}{1000 \: \text{J}} = 2.23 \: \text{kJ}\nonumber \]
- \[\Delta H_2 = 2.00 \: \text{mol} \times \frac{6.01 \: \text{kJ}}{1 \: \text{mol}} = 12.0 \: \text{kJ}\nonumber \]
- \[\Delta H_3 = 4.18 \: \text{J/g}^\text{o} \text{C} \times 36.04 \: \text{g} \times 100^\text{o} \text{C} \times \frac{1 \: \text{kJ}}{1000 \: \text{kJ}} = 15.1 \: \text{kJ}\nonumber \]
- \[\Delta H_4 = 2.00 \: \text{mol} \times \frac{40.7 \: \text{kJ}}{1 \: \text{mol}} = 81.4 \: \text{kJ}\nonumber \]
- \[\Delta H_5 = 1.87 \: \text{J/g}^\text{o} \text{C} \times 36.04 \: \text{g} \times 40^\text{o} \text{C} \times \frac{1 \: \text{kJ}}{1000 \: \text{J}} = 2.70 \: \text{kJ}\nonumber \]
\[\Delta H_\text{total} = \Delta H_1 + \Delta H_2 + \Delta H_3 + \Delta H_4 + \Delta H_5 = 113.4 \: \text{kJ}\nonumber \]
Step 3: Think about your result.
The total heat absorbed as the ice at \(-30^\text{o} \text{C}\) is heated to steam at \(140^\text{o} \text{C}\) is \(133.4 \: \text{kJ}\). The largest absorption of heat comes during the vaporization of the liquid water.

