17.10: Heats of Fusion and Solidification
- Page ID
- 53878
Suppose that you are holding an ice cube in your hand. It feels cold because heat energy leaves your hand and enters the ice cube. What happens to the ice cube? It melts. However, the temperature during a phase change remains constant. So the heat that is being lost by your hand does not raise the temperature of the ice above its melting temperature of \(0^\text{o} \text{C}\). Rather, all the heat goes into the change of state. Energy is absorbed during the process of changing ice into water. The water that is produced also remains at \(0^\text{o} \text{C}\) until all of the ice is melted.
Heats of Fusion and Solidification
All solids absorb heat as they melt to become liquids. The gain of heat in this endothermic process goes into changing the state, rather than changing the temperature. The molar heat of fusion \(\left( \Delta H_\text{fus} \right)\) of a substance is the heat absorbed by one mole of that substance as it is converted from a solid to a liquid. Since the melting of any substance absorbs heat, it follows that the freezing of any substance releases heat. The molar heat of solidification \(\left( \Delta H_\text{solid} \right)\) of a substance is the heat released by one mole of that substance as it is converted from a liquid to a solid. Since fusion and solidification of a given substance are the exact opposite processes, the numerical value of the molar heat of fusion is the same as the numerical value of the molar heat of solidification, but opposite in sign. In other words, \(\Delta H_\text{fus} = - \Delta H_\text{solid}\). The figure below shows all of the possible changes of state along with the direction of heat flow during each process.
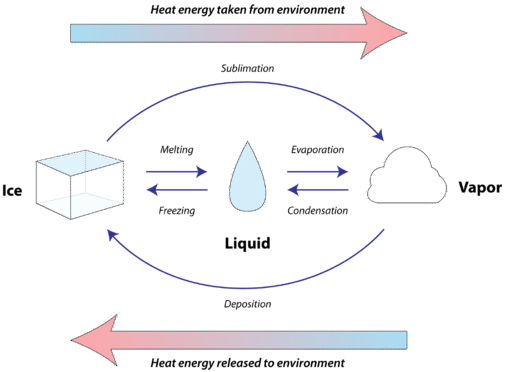
Every substance has a unique value for its molar heat of fusion, depending on the amount of energy required to disrupt the intermolecular forces present in the solid. When \(1 \: \text{mol}\) of ice at \(0^\text{o} \text{C}\) is converted to \(1 \: \text{mol}\) of liquid water at \(0^\text{o} \text{C}\), \(6.01 \: \text{kJ}\) of heat are absorbed from the surroundings. When \(1 \: \text{mol}\) of water at \(0^\text{o} \text{C}\) freezes to ice at \(0^\text{o} \text{C}\), \(6.01 \: \text{kJ}\) of heat is released into the surroundings.
\[\begin{array}{ll} \ce{H_2O} \left( s \right) \rightarrow \ce{H_2O} \left( l \right) & \Delta H_\text{fus} = 6.01 \: \text{kJ/mol} \\ \ce{H_2O} \left( l \right) \rightarrow \ce{H_2O} \left( s \right) & \Delta H_\text{solid} = -6.01 \: \text{kJ/mol} \end{array}\nonumber \]
The molar heats of fusion and solidification of a given substance can be used to calculate the heat absorbed or released when various amounts are melted or frozen.
Example \(\PageIndex{1}\)
Calculate the heat absorbed when \(31.6 \: \text{g}\) of ice at \(0^\text{o} \text{C}\) is completely melted.
Solution
Step 1: List the known quantities and plan the problem.
Known
- Mass \(= 31.6 \: \text{g}\) ice
- Molar mass \(\ce{H_2O} = 18.02 \: \text{g/mol}\)
- Molar heat of fusion \(= 6.01 \: \text{kJ/mol}\)
Unknown
The mass of ice is first converted to moles. This is then multiplied by the conversion factor of \(\left( \frac{6.01 \: \text{kJ}}{1 \: \text{mol}} \right)\) in order to find the \(\text{kJ}\) of heat absorbed.
Step 2: Solve.
\[31.6 \: \text{g ice} \times \frac{1 \: \text{mol ice}}{18.02 \: \text{g ice}} \times \frac{6.01 \: \text{kJ}}{1 \: \text{mol ice}} = 10.5 \: \text{kJ}\nonumber \]
Step 3: Think about your result.
The given quantity is a bit less than 2 moles of ice, and so just less than \(12 \: \text{kJ}\) of heat is absorbed by the melting process.
Summary
- The molar heat of fusion \(\left( \Delta H_\text{fus} \right)\) of a substance is the heat absorbed by one mole of that substance as it is converted from a solid to a liquid.
- The molar heat of solidification \(\left( \Delta H_\text{solid} \right)\) of a substance is the heat released by one mole of that substance as it is converted from a liquid to a solid.
- Calculations of heat changes during fusion and solidification are described.

