14.13: Gas Collection by Water Displacement
- Page ID
- 53834
Imagine that you need to do a lab experiment where hydrogen gas is generated. In order to calculate the yield of gas, you have to know the pressure inside the tube where the gas is collected. But how can you get a barometer in there? Very simple—you don't. All you need is the atmospheric pressure in the room. As the gas pushes out the water, it is pushing against the atmosphere, so the pressure inside is equal to the pressure outside.
Gas Collection by Water Displacement
Gases that are produced in laboratory experiments are often collected by a technique called water displacement (see figure below). A bottle is filled with water and placed upside-down in a pan of water. The reaction flask is fitted with rubber tubing which is then fed under the bottle of water. As the gas is produced in the reaction flask, it exits through the rubber tubing and displaces the water in the bottle. When the bottle is full of the gas, it can be sealed with a lid.
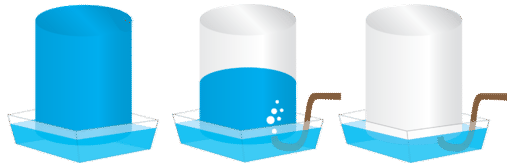
Because the gas is collected over water, it is not pure, but is mixed with vapor from the evaporation of the water. Dalton's law can be used to calculate the amount of the desired gas by subtracting the contribution of the water vapor:
\[\begin{array}{ll} P_\text{Total} = P_g + P_{H_2O} & P_g \: \text{is the pressure of the desired gas} \\ P_g = P_{Total} - P_{H_2O} & \end{array}\nonumber \]
In order to solve a problem, it is necessary to know the vapor pressure of water at the temperature of the reaction (see table below). The sample problem illustrates the use of Dalton's law when a gas is collected over water.
| Table \(\PageIndex{1}\): Vapor Pressure of Water \(\left( \text{mm} \: \ce{Hg} \right)\) at Selected Temperatures \(\left( ^\text{o} \text{C} \right)\) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 |
| 4.58 | 6.54 | 9.21 | 12.79 | 17.54 | 23.76 | 31.82 | 42.18 | 55.32 | 71.88 | 92.51 | 118.04 | 149.38 |
Example \(\PageIndex{1}\)
A certain experiment generates \(2.58 \: \text{L}\) of hydrogen gas, which is collected over water. The temperature is \(20^\text{o} \text{C}\) and the atmospheric pressure is \(98.60 \: \text{kPa}\). Find the volume that the dry hydrogen would occupy at STP.
Solution
Step 1: List the known quantities and plan the problem.
Known
- \(V_\text{Total} = 2.58 \: \text{L}\)
- \(T = 20^\text{o} \text{C} = 293 \: \text{K}\)
- \(P_\text{Total} = 98.60 \: \text{kPa} = 739.7 \: \text{mm} \: \ce{Hg}\)
Unknown
The atmospheric pressure is converted from \(\text{kPa}\) to \(\text{mm} \: \ce{Hg}\) in order to match units with the table. The sum of the pressures of the hydrogen and the water vapor is equal to the atmospheric pressure. The pressure of the hydrogen is found by subtraction. Then, the volume of the gas at STP can be calculated by using the combined gas law.
Step 2: Solve.
\[P_{H_2} = P_\text{Total} - P_{H_2O} = 739.7 \: \text{mm} \: \ce{Hg} - 17.54 \: \text{mm} \: \ce{Hg} = 722.2 \: \text{mm} \: \ce{Hg}\nonumber \]
Now the combined gas law is used, solving for \(V_2\), the volume of hydrogen at STP.
\[V_2 = \frac{P_1 \times V_1 \times T_2}{P_2 \times T_1} = \frac{722.2 \: \text{mm} \: \ce{Hg} \times 2.58 \: \text{L} \times 273 \: \text{K}}{760 \: \text{mm} \: \ce{Hg} \times 293 \: \text{K}} = 2.28 \: \text{L} \: \ce{H_2}\nonumber \]
Step 3: Think about your result.
If the hydrogen gas were to be collected at STP and without the presence of the water vapor, its volume would be \(2.28 \: \text{L}\). This is less than the actual collected volume because some of that is water vapor. The conversion using STP is useful for stoichiometry purposes.
Summary
- Gases that are produced in laboratory experiments are often collected by a technique called water displacement.
- The vapor pressure due to water in a sample can be corrected for in order to get the true value of the pressure of the gas.

