9.22: Hybrid Orbitals - sp³
- Page ID
- 53761

Do you recognize this plant?
If we were walking on the beach, the plants shown above would look very different. They would be short and sticking out of the sand. When we see them this way, we may not immediately recognize them as beach plants. Often, we need to look at the world around us in different ways to understand things better.
Hybrid Orbitals - sp3
The bonding scheme described by valence bond theory must account for molecular geometries as predicted by VSEPR theory. To do that, we must introduce the concept of hybrid orbitals.
\(sp^3\) Hybridization
Unfortunately, overlap of existing atomic orbitals (\(s\), \(p\), etc.) is not sufficient to explain some of the bonding and molecular geometries that are observed. Consider the element carbon and the methane \(\left( \ce{CH_4} \right)\) molecule. A carbon atom has the electron configuration of \(1s^2 \: 2s^2 \: 2p^2\), meaning that it has two unpaired electrons in its \(2p\) orbitals, as shown in the figure below.
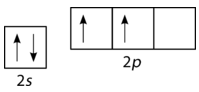
According to the description of valence bond theory so far, carbon would be expected to form only two bonds, corresponding to its two unpaired electrons. However, methane is a common and stable molecule, with four equivalent \(\ce{C-H}\) bonds. To account for this, one of the \(2s\) electrons is promoted to the empty \(2p\) orbital (see figure below).
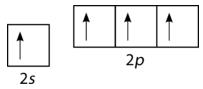
Now, four bonds are possible. The promotion of the electron "costs" a small amount of energy, but recall that the process of bond formation is accompanied by a decrease in energy. The two extra bonds that can now be formed results in a lower overall energy, and thus greater stability to the \(\ce{CH_4}\) molecule. Carbon normally forms four bonds in most of its compounds.
The number of bonds is now correct, but the geometry is wrong. The three \(p\) orbitals, (\(p_x\), \(p_y\), and \(p_z\)), are oriented at \(90^\text{o}\) relative to one another. However, as seen in VSEPR theory, the observed \(\ce{H-C-H}\) bond angle in the tetrahedral \(\ce{CH_4}\) molecule is actually \(109.5^\text{o}\). Therefore, the methane molecule cannot be adequately represented by simple overlap of the \(2s\) and \(2p\) orbitals of carbon with the \(1s\) orbitals of each hydrogen atom.
To explain the bonding in methane, it is necessary to introduce the concept of hybridization and hybrid atomic orbitals. Hybridization is the mixing of the atomic orbitals in an atom to produce a set of hybrid orbitals. When hybridization occurs, it must do so as a result of the mixing of nonequivalent orbitals. In other words, \(s\) and \(p\) orbitals can hybridize, but \(p\) orbitals cannot hybridize with other \(p\) orbitals. Hybrid orbitals are the atomic orbitals obtained when two or more nonequivalent orbitals from the same atom combine in preparation for bond formation. In the current case of carbon, the single \(2s\) orbital hybridizes with the three \(2p\) orbitals to form a set of four hybrid orbitals, called \(sp^3\) hybrids (see figure below).
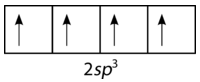
The \(sp^3\) hybrids are all equivalent to one another. Spatially, the hybrid orbitals point towards the four corners of a tetrahedron (see figure below).

Summary
- Electrons hybridize in order to form covalent bonds.
- Nonequivalent orbitals mix to form hybrid orbitals.
Review
- Why is carbon expected to form only two covalent bonds?
- How many covalent bonds does carbon actually form?
- What needs to happen to allow carbon to form four bonds?

