7.2: State Changes and Energy
- Last updated
- Save as PDF
- Page ID
- 155669
Learning Outcomes
- Identify whether energy is consumed or released during a phase change.
- Calculate the amount of energy consumed or released during a phase change.
- Recognize that the enthalpies of vaporization and condensation are equal in magnitude but opposite in sign.
- Recognize that the enthalpies of fusion and freezing are equal in magnitude but opposite in sign.
Heating Curve
When heat energy is supplied to a solid (like ice) at a steady rate by means of an electrical heating coil, we find that the temperature climbs steadily until the melting point is reached and the first signs of liquid formation become evident. Thereafter, even though we are still supplying heat energy to the system, the temperature remains constant as long as both liquid and solid are present. On the graph below, this is represented by the flat line, where energy is being added to the ice, but no change is occurring in the temperature. All energy added to the system at this stage is used to convert solid ice into liquid water.
Once all of the sample is in the liquid phase, the addition of energy now increases the temperature until the boiling point is reached and the first signs of gas formation are seen. The temperature remains constant even though energy is being added to the system. The energy is being used to convert the liquid to a gas. Once all of the sample is in the gas phase, additional energy can be added to increase the temperature of the gas.
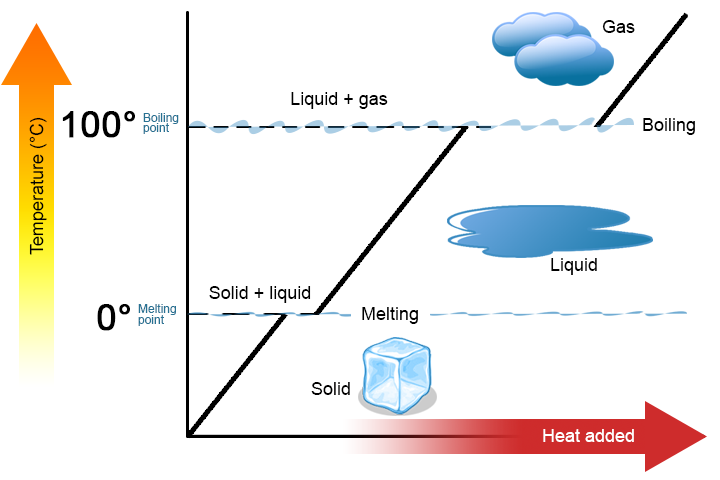
This macroscopic behavior demonstrates quite clearly that energy must be supplied to a solid in order to melt or vaporize it. On a microscopic level melting or vaporization involves separating molecules which are attracted to each other. The amount of energy needed to separate the molecules is proportional to the intermolecular forces between the molecules.
Enthalpy
The heat energy which a solid absorbs when it melts is called the enthalpy of fusion (or heat of fusion and is usually quoted on a molar basis. (The word fusion means the same thing as “melting.”) When 1 mol of ice, for example, is melted, we find from experiment that 6.01 kJ of energy is needed. The molar enthalpy of fusion of ice is thus +6.01 kJ per mol (\(\dfrac{6.01\;kJ}{mol}\)), and we can write
\[\text{H}_{2}\text{O}(s) \rightarrow \text{H}_{2}\text{O}(l)\]
\[\triangle H_{fus} = \dfrac{6.01\;kJ}{mol}\]
If two moles of water are melted, then it would require twice as much energy (see below). The amount of energy needed to melt a substance will depend on the amount of the substance.
\(2\;mol\times \dfrac{6.01\;kJ}{mol}=\dfrac{12.0\;kJ}{mol}\)
Selected molar enthalpies of fusion are tabulated in Table \(\PageIndex{1}\). Solids like ice which have strong intermolecular forces have much higher values than those like CH4 with weak ones.
When a liquid is boiled (or vaporized), energy is required to move the molecules apart to go from the liquid phase to the gas phase. The energy which a liquid absorbs when it vaporizes is known as the enthalpy of vaporization (. In the case of water, the molar enthalpy of vaporization is (\(\dfrac{40.67\;kJ}{mol}\)). In other words
\[\text{H}_{2}\text{O}(s) \rightarrow \text{H}_{2}\text{O}(l)\]
\[\triangle H_{vap} = 40.67 \dfrac {\text{kJ}}{\text{mol}}\]
Heat energy is absorbed to vaporize a liquid because molecules which are held together by intermolecular forces in the liquid are separated as the gas is formed. Such a separation requires energy. As with melting, the amount of energy needed to vaporize a substance is proportional to the amount of substance present. The more liquid there is, the more energy required to vaporize it.
In general the energy needed differs from one liquid to another depending on the magnitude of the intermolecular forces. We can expect liquids with strong intermolecular forces to have larger enthalpies of vaporization. See the examples in the table below. Note that the enthalpy of vaporization of a substance is always higher than its enthalpy of fusion. When a solid melts, the molecules are not separated from each other to nearly the same extent as when a liquid boils.
Melting and boiling points are given in units of Kelvin (\(K = T_{^{\circ}C}\;+\;273.15 \))
*http://www1.lsbu.ac.uk/water/data.html
Example \(\PageIndex{1}\): Heat Energy
Calculate the heat energy required to (a) vaporize 100. g of lead, (b) melt 100. g of lead, (c) vaporize 100. g water, and (d) melt 100. g of water.
Solution
(a)To vaporize 100. g of lead:
\[\text{Pb}(l) \rightarrow\text{Pb}(g)\;\;\;\;\;\;\;\;\;\;
\triangle H_{vap} = 178 \dfrac {kJ}{mol}\]
\[100.\;g\times\dfrac {1\;mol\;\text{Pb}}{207.2\;g\;\text{Pb}}\times \dfrac{178\;{kJ}}{mol} = 85.9\; kJ\]
(b) To melt 100. g of lead:
\[\text{Pb}(s) \rightarrow\text{Pb}(l)\;\;\;\;\;\;\;\;\;\;\triangle H_{fus} = 4.77 \dfrac {kJ}{mol}\]
\[100.\;g\times\dfrac {1\;mol\;\text{Pb}}{207.2\;g\;\text{Pb}}\times \dfrac{4.77\;{kJ}}{mol} = 2.30\; kJ\]
(c) To vaporize 100. g of water:
\[\text{H}_2\text{O}(s) \rightarrow\text{H}_2\text{O}(l)\;\;\;\;\;\;\;\;\;\;\triangle H_{vap} =40.657\dfrac {kJ}{mol}\]
\[100.\;g\times\dfrac {1\;mol\;\text{H}_2\text{O}}{18.0\;g\;\text{H}_2\text{O}}\times \dfrac{40.657\;{kJ}}{mol} = 226\; kJ\]
(d) To melt 100. g of water:
\[\text{H}_2\text{O}(s) \rightarrow\text{H}_2\text{O}(l)\;\;\;\;\;\;\;\;\;\;\triangle H_{fus} = 6.01 \dfrac {kJ}{mol}\]
\[100.\;g\times\dfrac {1\;mol\;\text{H}_2\text{O}}{18.0\;g\;\text{H}_2\text{O}}\times \dfrac{6.01\;{kJ}}{mol} = 33.4\; kJ\]
It might be surprising that the heat required to melt or vaporize 100 g of lead is so much less than that require to melt or vaporized water. First, the temperature at which the substance melts has nothing to do with the enthalpy of fusion. Remember, we are only looking at the energy required to change the phase, not the energy required to get the substance to the melting or boiling point.
Also note that the enthalpies of fusion and vaporization are given as kJ per mole. Although the water and the lead have the same mass, the moles of each substance is very different (5.5 moles of water vs. 0.48 moles of lead).
Freezing and Condensation
The discussion here has focused on fusion (melting) and vaporization. But what about freezing and condensation? Fusion (solid to liquid) and freezing (liquid to solid) are opposite processes. As a result, the magnitude of energy for each is the same, but the sign is different. With fusion, energy is a positive value because it is endothermic (consuming energy) while the energy for freezing is negative because it is an exothermic process (releasing energy).
Let's compare the enthalpies of fusion and freezing for methane. Both values have the same magnitude of 0.94 but they have the opposite sign.
\(\triangle H_{fusion}=0.94\;\dfrac{kJ}{mol}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\triangle H_{freezing}=-0.94\;\dfrac{kJ}{mol}\)
The same concept applies to vaporization (liquid to gas) and condensation (gas to liquid). Energy is consumed during vaporization (positive energy) and released during condensation (negative energy). The enthalpies of vaporization and condensation are equal in magnitude but opposite in sign.
\(\triangle H_{vaporization}=8.18\;\dfrac{kJ}{mol}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\triangle H_{condensation}=-8.18\;\dfrac{kJ}{mol}\)
Energy is consumed to change a substance from solid to liquid to gas. Energy is released to change a substance from gas to liquid to solid.
Contributors and Attributions
Ed Vitz (Kutztown University), John W. Moore (UW-Madison), Justin Shorb (Hope College), Xavier Prat-Resina (University of Minnesota Rochester), Tim Wendorff, and Adam Hahn.
Allison Soult, Ph.D. (Department of Chemistry, University of Kentucky)

