Identifying Planes of Symmetry in Octahedral Complexes
- Page ID
- 81965
The symmetry of a molecule is determined by the existence of symmetry operations performed with respect to symmetry elements. A symmetry element is a line, a plane or a point in or through an object, about which a rotation or reflection leaves the object in an orientation indistinguishable from the original. A plane of symmetry and the reflection operation is the coincidence of atoms on one side of the plane with corresponding atoms on the other side, as though reflected in a mirror.
Nine Planes of Potential Symmetry
Identifying planes of symmetry in an octahedral geometry can be daunting in evaluating if a molecule is chiral or not. There is a simple approach, which requires identying and testing six possible planes of symmetry that may exist for this geometry. To demonstrated this, we will consider the \(\ce{[Cr(CO)6]}\) complex in Figure \(\PageIndex{1}\).
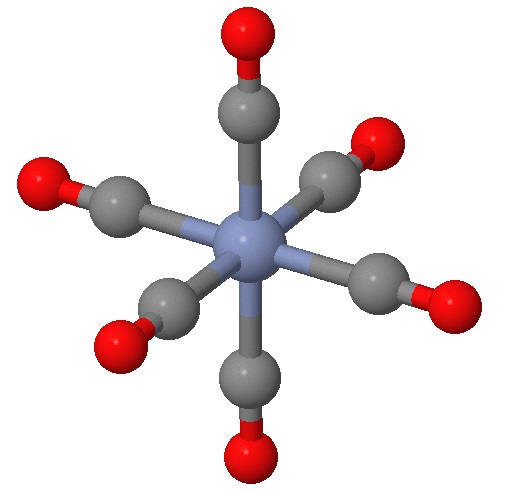
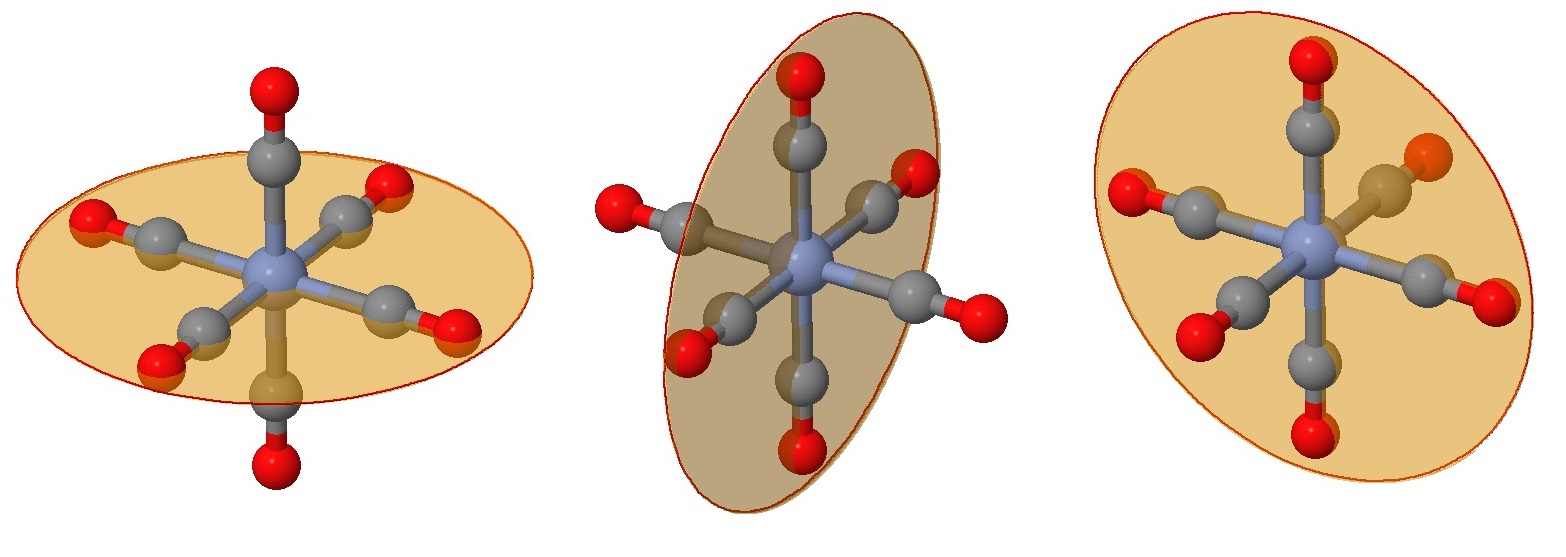
While you can no doubt recognize at least one plane of symmetry to confirm that this is an achiral complex, let's identify all six of them. First we have the three planes that include the \(Cr\) metal center (as they all do) and four of the attached ligands (Figure \(\PageIndex{2}\)). These are often the easy planes to identify.
The next six planes are harder to identify and can be viewed as rotations of those in Figure \(\PageIndex{2}\) by 45°. These planes bisect one angle between ligands, but still have two ligands on the plane (instead of four in the planes of Figure \(\PageIndex{2}\)).
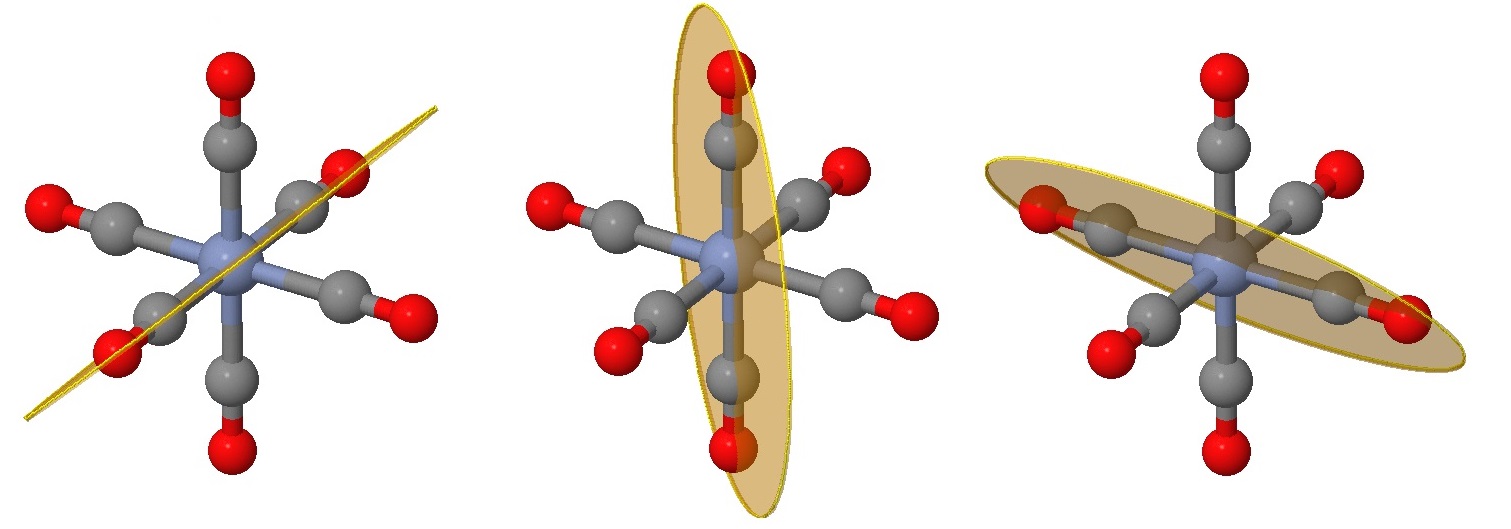
The next three planes are even harder to view on the same perspective but are also rotations of those in Figure \(\PageIndex{2}\) by 45° in the perpendicular direction. These planes bisect an angle between ligands, but still have two ligands on the plane.
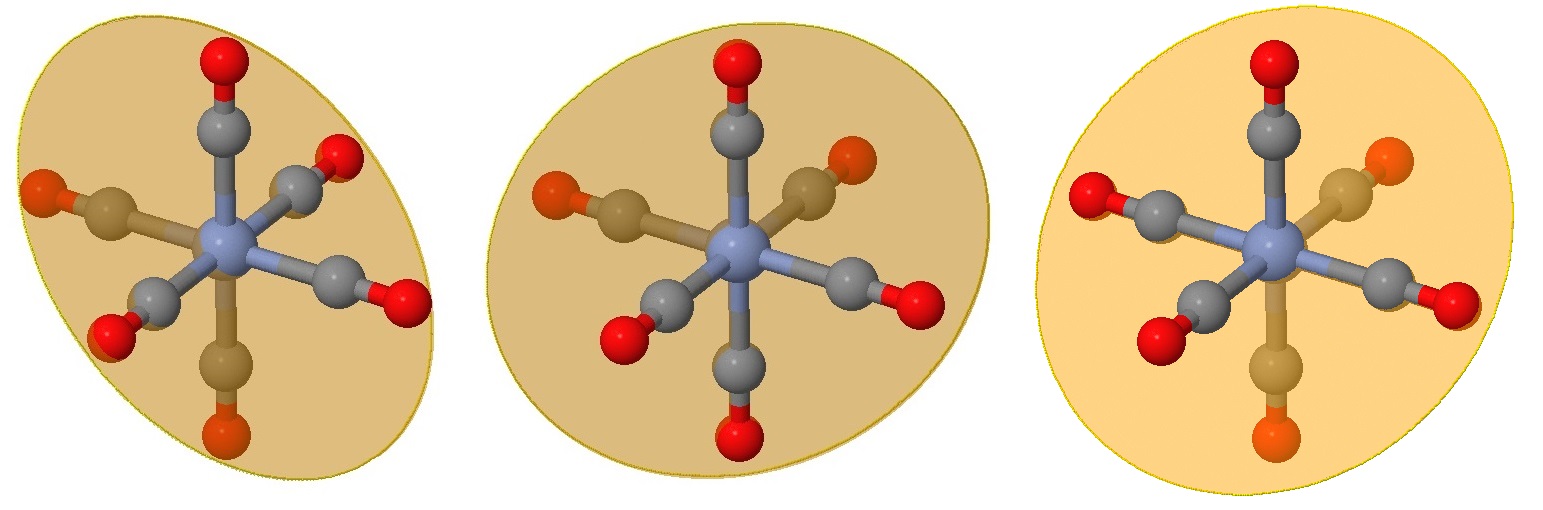
All nine planes, in each of planes are combined in the images below.
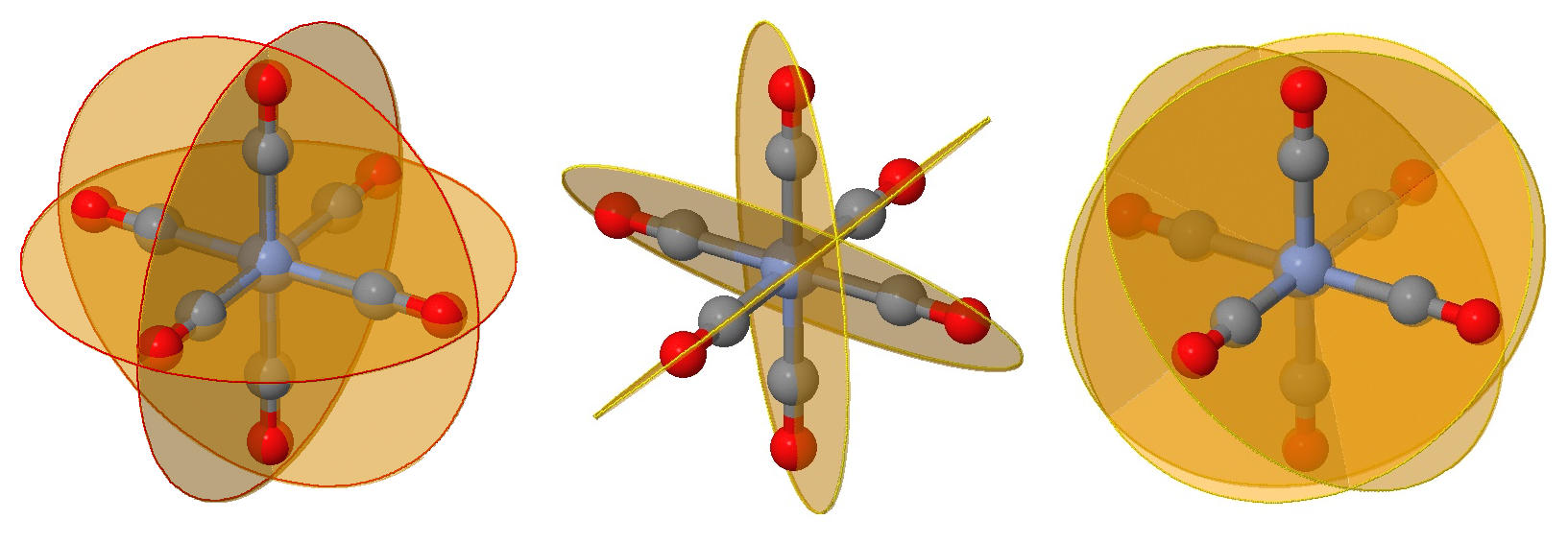
Now that can you identify these nine planes that may be mirror planes in an octahedral complex, you have to evaluate if they truly are mirror planes. That is simply asking if the ligand fields above the plane is IDENTICAL to the ligand field below. For the \(\ce{[Cr(CO)]}\) complex discussed above, all nine planes are indeed mirror planes. However, in other complexes that may not be the case. Fortunately, to determine if a complex is chiral (optically active), then only one plane needs to be identified.
Contributors and Attributions
William Reusch, Professor Emeritus (Michigan State U.), Virtual Textbook of Organic Chemistry

