4.4.2: Molecular Vibrations
- Page ID
- 236072
Symmetry and group theory can be applied to understand molecular vibrations. This is particularly useful in the context of predicting the number of peaks expected in the infrared (IR) and Raman spectra of a given compound.
We will use water as a case study to illustrate how group theory is used to predict the number of peaks in IR and Raman spectra.
How many IR and Raman peaks would we expect for \(H_2O\)?
To answer this question with group theory, a pre-requisite is that you assign the molecule's point group and assign an axis system to the entire molecule. By convention, the \(z\) axis is collinear with the principle axis, the \(x\) axis is in-plane with the molecule or the most number of atoms. It is a good idea to stick with this convention (see Figure \(\PageIndex{1}\)).
- What is the point group for \(H_2O\)? (click to see answer)
-
\(H_2O\) has the following operations: \(E\), \(C_2\), \(\sigma_v\), \(\sigma_v'\). The point group is \(C_{2v}\).
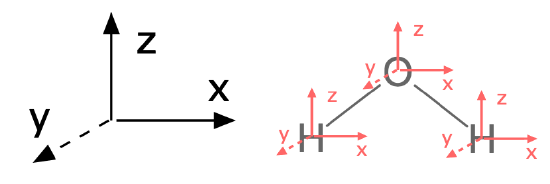
Figure \(\PageIndex{1}\): The first step to finding normal modes is to assign a consistent axis system to the entire molecule and to each atom. (CC-BY-SA; Kathryn Haas)
Now that we know the molecule's point group, we can use group theory to determine the symmetry of all motions in the molecule, or the symmetry of each of its degrees of freedom. Then we will subtract rotational and translational degrees of freedom to find the vibrational degrees of freedom. The number of degrees of freedom depends on the number of atoms (\(N\)) in a molecule. Each atom in the molecule can move in three dimensions (\(x,y,z\)), and so the number of degrees of freedom is three dimensions times \(N\) number of atoms, or \(3N\). The total degrees of freedom include a number of vibrations, three translations (in \(x\), \(y\), and \(z\)), and either two or three rotations. Linear molecules have two rotational degrees of freedom, while non-linear molecules have three. The vibrational modes are represented by the following expressions:
\[\begin{array}{ccc} \text{Linear Molecule Degrees of Freedom} & = & 3N - 5 \\ \text{Non-Linear Molecule Degrees of Freedom} & = & 3N-6 \end{array} \nonumber \]
Our goal is to find the symmetry of all degrees of freedom, and then determine which are vibrations that are IR- and Raman-active.
STEP 1: Find the reducible representation for all normal modes \(\Gamma_{modes}\).
The first major step is to find a reducible representation (\(\Gamma\)) for the movement of all atoms in the molecule (including rotational, translational, and vibrational degrees of freedom). We'll refer to this as \(\Gamma_{modes}\). To find normal modes using group theory, assign an axis system to each individual atom to represent the three dimensions in which each atom can move. Each axis on each atom should be consistent with the conventional axis system you previously assigned to the entire molecule (see Figure \(\PageIndex{1}\)).
\(\Gamma_{modes}\) is the sum of the characters (trace) of the transformation matrix for the entire molecule (in the case of water, there are 9 degrees of freedom and this is now a 9x9 matrix). Let's walk through this step-by-step. The transformation matrix of \(E\) and \(C_2\) are shown below:
\[E=\begin{pmatrix} \color{red}1&0&0&0&0&0&0&0&0 \\ 0&\color{red}1&0&0&0&0&0&0&0 \\ 0&0&\color{red}1&0&0&0&0&0&0 \\0&0&0&\color{red}1&0&0&0&0&0 \\ 0&0&0&0&\color{red}1&0&0&0&0 \\ 0&0&0&0&0&\color{red}1&0&0&0 \\ 0&0&0&0&0&0&\color{red}1&0&0 \\ 0&0&0&0&0&0&0&\color{red}1&0 \\ 0&0&0&0&0&0&0&0&\color{red}1 \\ \end{pmatrix} \begin{pmatrix} x_{oxygen} \\ y_{oxygen} \\ z_{oxygen} \\ x_{hydrogen-a} \\ y_{hydrogen-a} \\ z_{hydrogen-a} \\ x_{hydrogen-b} \\ y_{hydrogen-b} \\ z_{hydrogen-b} \end{pmatrix} = \begin{pmatrix} x'_{oxygen} \\ y'_{oxygen} \\ z'_{oxygen} \\ x'_{hydrogen-a} \\ y'_{hydrogen-a} \\ z'_{hydrogen-a} \\ x'_{hydrogen-b} \\ y'_{hydrogen-b} \\ z'_{hydrogen-b} \end{pmatrix}, \chi=9 \nonumber \]
\[C_2=\begin{pmatrix} \color{red}-1&0&0&0&0&0&0&0&0 \\ 0&\color{red}-1&0&0&0&0&0&0&0 \\ 0&0&\color{red}1&0&0&0&0&0&0 \\0&0&0&\color{red}0&0&0&-1&0&0 \\ 0&0&0&0&\color{red}0&0&0&-1&0 \\ 0&0&0&0&0&\color{red}0&0&0&1 \\ 0&0&0&-1&0&0&\color{red}0&0&0 \\ 0&0&0&0&-1&0&0&\color{red}0&0 \\ 0&0&0&0&0&1&0&0&\color{red}0 \\ \end{pmatrix} \begin{pmatrix} x_{oxygen} \\ y_{oxygen} \\ z_{oxygen} \\ x_{hydrogen-a} \\ y_{hydrogen-a} \\ z_{hydrogen-a} \\ x_{hydrogen-b} \\ y_{hydrogen-b} \\ z_{hydrogen-b} \end{pmatrix} = \begin{pmatrix} x'_{oxygen} \\ y'_{oxygen} \\ z'_{oxygen} \\ x'_{hydrogen-a} \\ y'_{hydrogen-a} \\ z'_{hydrogen-a} \\ x'_{hydrogen-b} \\ y'_{hydrogen-b} \\ z'_{hydrogen-b} \end{pmatrix}, \chi=1 \nonumber \]
It is unnecessary to find the transformation matrix for each operation since it is only the TRACE that gives us the character, and any off-diagonal entries do not contribute to \(\Gamma_{modes}\). The values that contribute to the trace can be found simply by performing each operation in the point group and assigning a value to each individual atom to represent how it is changed by that operation. If the atom moves away from itself, that atom gets a character of zero (this is because any non-zero characters of the transformation matrix are off of the diagonal). If the atom remains in place, each of its three dimensions is assigned a value of \(\cos \theta\). For the example of \(H_2O\) under the \(C_{2v}\) point group, the axes that remain unchanged (\(\theta = 0^{\circ}\)) are assigned a value of \(\cos(0^{\circ})=1\), while those that are moved into the negative of themselves (rotated or reflected to \( \theta = 180^{\circ}\)) are assigned \(\cos(180^{\circ}) = -1\). The character for \(\Gamma\) is the sum of the values for each transformation.
Let's walk through the steps to assign characters of \(\Gamma_{modes}\) for \(H_2O\) to illustrate how this works:
For the operation \(E\), performed on \(H_2O\), all three atoms remain in place. The three axes \(x,y,z\) on each atom remain unchanged. Thus, each of the three axes on each of three atom (nine axes) is assigned the value \(\cos(0^{\circ})=1\), resulting in a sum of \(\chi=9\) for the \(\Gamma_{modes}\).
For the operation \(C_2\), the two hydrogen atoms are moved away from their original position, and so the hydrogens are assigned a value of zero. The oxygen remains in place; the \(z\)-axis on oxygen is unchanged (\(\cos(0^{\circ})=1\)), while the \(x\) and \(y\) axes are inverted (\(\cos(180^{\circ})\)). The sum of these characters gives \(\chi=-1\) in the \(\Gamma_{modes}\).
Now you try! Find the characters of \(\sigma_{v(xz)}\) and \(\sigma_{v(yz)}\) under the \(C_{2v}\) point group. Compare what you find to the \(\Gamma_{modes}\) for all normal modes given below.
\[\begin{array}{l|llll} C_{2v} & E & C_2 & \sigma_v & \sigma_v' \\ \hline \Gamma_{modes} & 9 & -1 & 3 & 1 \end{array} \label{gammamodes} \]
STEP 2: Break \(\Gamma_{modes}\) into its component irreducible representations.
Now that we've found the \(\Gamma_{modes}\) (\(\ref{gammamodes}\)), we need to break it down into the individual irreducible representations (\(i,j,k...\)) for the point group. We can do this systematically using the following formula:
\[\text{# of } i = \frac{1}{h}\sum(\text{# of operations in class)}\times(\chi_{\Gamma}) \times (\chi_i) \label{irs} \]
In other words, the number of irreducible representations of type \(i\) is equal to the sum of the number of operations in the class \(\times\) the character of the \(\Gamma_{modes}\) \(\times\) the character of \(i\), and that sum is divided by the order of the group (\(h\)).
Using equation \(\ref{irs}\), we find that for all normal modes of \(H_2O\):
\[\Gamma_{modes}=3A_1+1A_2+3B_1+2B_2 \label{water} \].
Notice there are 9 irreducible representations in Equation \ref{water}. These irreducible representations represent the symmetries of all 9 motions of the molecule: vibrations, rotations, and translations.
Derive the nine irreducible representations of \(\Gamma_{modes}\) for \(H_2O\), expression \(\ref{water}\).
- Hint
-
To find the number of each kind of irreducible representation that combine to form the \(\Gamma_{modes}\), we need the characters of \(\Gamma_{modes}\) that we found above (\(\ref{gammamodes}\)), the \(C_{2v}\) character table (below), and equation \(\ref{irs}\).
\(\begin{array}{l|llll|l|l} C_{2v} & {\color{red}1}E & {\color{red}1}C_2 & {\color{red}1}\sigma_v & {\color{red}1}\sigma_v' & \color{orange}h=4\\ \hline \color{green}A_1 & \color{green}1 & \color{green}1 & \color{green}1 & \color{green}1 & \color{green}z & \color{green}x^2,y^2,z^2\\ \color{green}A_2 & \color{green}1 & \color{green}1 & \color{green}-1 & \color{green}-1 & \color{green}R_z & \color{green}xy \\ \color{green}B_1 & \color{green}1 & \color{green}-1&\color{green}1&\color{green}-1 & \color{green}x,R_y & \color{green}xz \\ \color{green}B_2 & \color{green}1 & \color{green}-1 & \color{green}-1 & \color{green}1 & {\color{green}y} ,\color{green}R_x & \color{green}yz \end{array} \)
In the \(C_{2v}\) point group, each class has only one operation, so the number of operations in each class (from equation \(\ref{irs}\)) is \({\color{red}1}\) for each class. This has been explicitly added to the character table above for emphasis.
- Answer
-
The number of \(A_1\) = \(\frac{1}{\color{orange}4} \left[ ({\color{green}1} \times 9 \times {\color{red}1}) + ({\color{green}1} \times (-1) \times {\color{red}1}) + ({\color{green}1} \times 3 \times {\color{red}1}) + ({\color{green}1} \times 1 \times {\color{red}1})\right] = 3A_1 \)
The number of \(A_2\) = \(\frac{1}{\color{orange}4} \left[ ({\color{green}1} \times 9 \times {\color{red}1}) + ({\color{green}1} \times (-1) \times {\color{red}1}) + ({\color{green}(-1)} \times 3 \times {\color{red}1}) + ({\color{green}(-1)} \times 1 \times {\color{red}1})\right] = 1A_2 \)
The number of \(B_1\) = \(\frac{1}{\color{orange}4} \left[ ({\color{green}1} \times 9 \times {\color{red}1}) + ({\color{green}(-1)} \times (-1) \times {\color{red}1}) + ({\color{green}1} \times 3 \times {\color{red}1}) + ({\color{green}(-1)} \times 1 \times {\color{red}1})\right] = 3B_1 \)
The number of \(B_2\) = \(\frac{1}{\color{orange}4} \left[ ({\color{green}1} \times 9 \times {\color{red}1}) + ({\color{green}(-1)} \times (-1) \times {\color{red}1}) + ({\color{green}(-1)} \times 3 \times {\color{red}1}) + ({\color{green}1} \times 1 \times {\color{red}1})\right] = 2B_2 \)
STEP 3: Subtract rotations and translations to find vibrational modes.
Because we are interested in molecular vibrations, we need to subtract the rotations and translations from the total degrees of freedom.
\[\text{Vibrations } = \Gamma_{modes}-\text{ Rotations } - \text{ Translations } \nonumber \]
In the example of \(H_2O\), the total degrees of freedom are given above in equation \(\ref{water}\), and therefore the vibrational degrees of freedom can be found by:
\[H_2O\text{ vibrations} = \left(3A_1 + 1A_2 + 3B_1 + 2B_2\right) - \text{ Rotations } - \text{ Translations } \label{watervib} \]
But which of the irreducible representations are ones that represent rotations and translations? The symmetry of rotational and translational degree modes can be found by inspecting the right-hand columns of any character table. Rotational modes correspond to irreducible representations that include \(R_x\), \(R_y\), and \(R_z\) in the table, while each of the three translational modes has the same symmetry as the \(x\), \(y\) and \(z\) axes. For a non-linear molecule, subtract three rotational irreducible representations and three translational irreducible representations from the total \(\Gamma_{modes}\).
In the specific case of water, we refer to the \(C_{2v}\) character table:
\[\begin{array}{l|llll|l|l} C_{2v} & E & C_2 & \sigma_v & \sigma_v' & h=4\\ \hline A_1 &1 & 1 & 1 & 1 & \color{red}z & x^2,y^2,z^2\\ A_2 & 1 & 1 & -1 & -1 & \color{red}R_z & xy \\ B_1 &1 & -1&1&-1 & \color{red}x,R_y &xz \\ B_2 & 1 & -1 &-1 & 1 & \color{red}y ,R_x & yz \end{array} \nonumber \]
In \(C_{2v}\), translations correspond to \(B_1\), \(B_2\), and \(A_1\) (respectively for \(x,yz\)), and rotations correspond to \(B_2\), \(B_1\), and \(A_1\) (respectively for \(R_x,R_y,R_z\)). Subtracting these six irreducible representations from \(\Gamma_{modes}\) will leave us with the irreducible representations for vibrations.
\[\begin{array}{lll} H_2O\text{ vibrations} &=& \Gamma_{modes} - \text{ Rotations } - \text{ Translations }\\ &=& \left(3A_1 + 1A_2 + 3B_1 + 2B_2\right) - (A_1 + B_1 + B_2) -(A_2 + B_1 + B_2) \\ &=& 2A_1 + 1B_1 \end{array} \nonumber \]
The three vibrational modes for \(H_2O\) are \(2A_1 + 1B_1\). Note that we have the correct number of vibrational modes based on the expectation of \(3N-6\) vibrations for a non-linear molecule.
STEP 4: Determine which of the vibrational modes are IR-active and Raman-active.
The next step is to determine which of the vibrational modes is IR-active and Raman-active. To do this, we apply the IR and Raman Selection Rules below:
Infrared selection rules:
If a vibration results in the change in the molecular dipole moment, it is IR-active. In the character table, we can recognize the vibrational modes that are IR-active by those with symmetry of the \(x,y\), and \(z\) axes.
In \(C_{2v}\), any vibrations with \(A_1\), \(B_1\) or \(B_2\) symmetry would be IR-active.
Raman selection rules:
If a vibration results in a change in the molecular polarizability, it will be Raman-active. In the character table, we can recognize the vibrational modes that are Raman-active by those with symmetry of any of the binary products (\(xy\), \(xz\), \(yz\), \(x^2\), \(y^2\), and \(z^2\)) or a linear combination of binary products (e.g. \(x^2-y^2\)).
In \(C_{2v}\), any vibrations with \(A_1\), \(A_2\), \(B_1\) or \(B_2\) symmetry would be Raman-active.
In our \(H_2O\) example, we found that of the three vibrational modes, two have \(A_1\) and one has \(B_1\) symmetry. Both \(A_1\) and \(B_1\) are IR-active, and both are also Raman-active. There are two possible IR peaks and three possible Raman peaks expected for water.*
*It is important to note that this prediction tells only what is possible, but not what we might actually see in the IR and Raman spectra. For example, if the two IR peaks overlap, we might actually notice only one peak in the spectrum. Or, if one or more peaks is off-scale, we wouldn't see it in actual data. Group theory tells us what is possible and allows us to make predictions or interpretations of spectra.
Summary of Analysis for Water
Each molecular motion for water, or any molecule, can be assigned a symmetry under the molecule's point group. For water, we found that there are a total of 9 molecular motions; \(3A_1 + A_2 +3B_1 + 2B_2\). Six of these motions are not the translations and rotations. The remaining motions are vibrations; two with \(A_1\) symmetry and one with \(B_1\) symmetry.
We can tell what these vibrations would look like based on their symmetries. The two \(A_1\) vibrations must be completely symmetric, while the \(B_1\) vibration is antisymmetric with respect to the principal \(C_2\) axis.

| All Motions (step 2 above) | Translations (x,y,z) | Rotations (\(R_x,R_y,R_z\)) | Remaining Vibrations | Description of Vibration |
|---|---|---|---|---|
| \(3A_1\) | \(1A_1\) | \(2A_1\) | One is a symmetric stretch. The other is a symmetric bend. Both are IR-active and Raman-active | |
| \(A_2\) | \(1A_2\) | |||
| \(3B_1\) | \(1B_1\) | \(1B_1\) | \(1B_1\) | Antisymmetric stretch that is IR-active and Raman-active. |
| \(2B_2\) | \(1B_2\) | \(1B_2\) |
Find the symmetries of all motions of the square planar complex, tetrachloroplatinate (II). Determine which are rotations, translations, and vibrations. Determine which vibrations are IR and Raman active.
- Answer
-
The point group of \(\ce{[PtCl4]^2-}\) is \(D_{4h}\) (refer to its character table). There are five atoms and 15 vectors (\(x,y,z\) for each atom \(\times\) 5 atoms).
STEP 1: The first major step is to find a reducible representation (\(\Gamma\)) for the movement of all atoms in the molecule.
\[\begin{array}{l|rrrrrrrrrr}
C_{2v} & E & 2C_4 & C_2 & 2C_2' & 2C_2" & i & 2S_4 & \sigma_h & 2\sigma_v & 2\sigma_d \\ \hline
\Gamma_{modes} & 15 & 1 & -1 & -3 & -1 & -3 & -1 & 5 & 3 & 1 \end{array} \label{gammamodes2} \].STEP 2: Break \(\Gamma_{modes}\) into its component irreducible representations.
Following the process described earlier, we come to \(A_{1g} + A_{2g} + B_{1g} + B_{2g} + E_g + 2A_{2u} + B_{2u} + 3E_u\). This accounts for all modes of movement, including rotations and translations.
STEP 3: Subtract rotations and translations to find vibrational modes.
The translations are \(A_{2u}+E_u\) and the rotations are \(A_{2g}+E_g\).
The remaining normal modes are: \( A_{1g} + B_{1g} + B_{2g} + A_{2u} + B_{2u} + 2 E_u \)STEP 4: Determine which of the vibrational modes are IR-active and Raman-active:
\(A_{2u} + E_u\) are IR-active. Since \(A_{2u}\) is singly degenerate and \(E_u\) is doubly degenerate, we expect three possible IR bands.
\(A_{1g} + B_{1g} + B_{2g}\) are Raman-Active. Each of these is singly degenerate, so we expect three possible Raman bands.
Selected Vibrational Modes
The interpretation of CO stretching vibrations in an IR spectrum is particularly useful. Symmetry and group theory can be applied to predict the number of CO stretching bands that appear in a vibrational spectrum for a given metal coordination complex. A classic example of this application is in distinguishing isomers of metal-carbonyl complexes. For example, the cis- and trans- isomers of square planar metal dicarbonyl complexes (ML2(CO)2) have a different number of IR stretches that can be predicted and interpreted using symmetry and group theory. Another example is the case of mer- and fac- isomers of octahedral metal tricarbonyl complexes (ML3(CO)3). Structures of the two types of metal carbonyl configurations and their isomers are shown in Figure \(\PageIndex{1}\). The isomers in each case can be distinguished using vibrational spectroscopy.
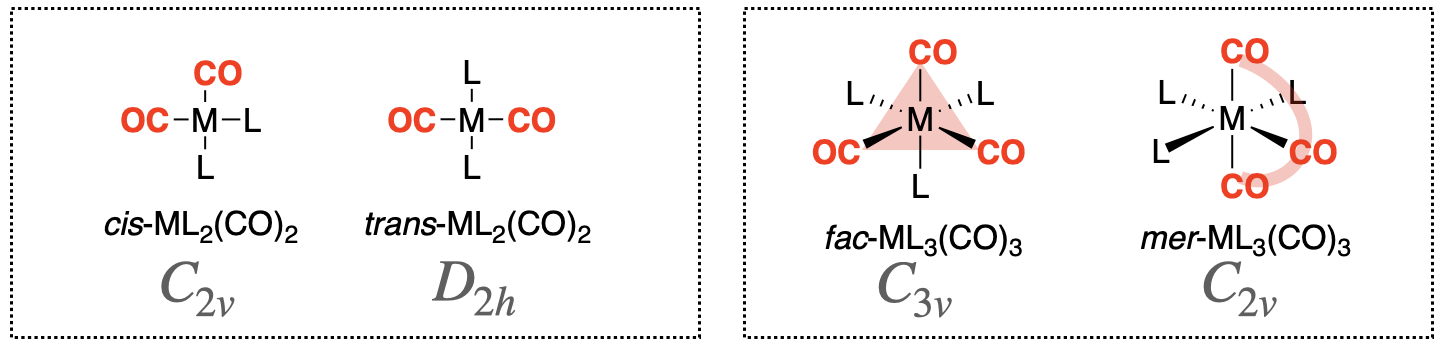
EXAMPLE 1: Distinguishing cis- and trans- isomers of square planar metal dicarbonyl complexes
General structures of the cis- and trans- isomers of square planar metal dicarbonyl complexes (ML2(CO)2) are shown in the left box in Figure \(\PageIndex{1}\). We can use symmetry and group theory to predict how many carbonyl stretches we should expect for each isomer following the steps below.
Step 1: Assign the point group and Cartesian coordinates for each isomer.
The cis-isomer has \(C_{2v}\) symmetry and the trans-isomer has \(D_{2h}\) symmetry. We assign the Cartesian coordinates so that \(z\) is colinear with the principle axis in each case. For the \(D_2{h}\) isomer, there are several orientations of the \(z\) axis possible. The axes shown in Figure \(\PageIndex{2}\) will be used here.
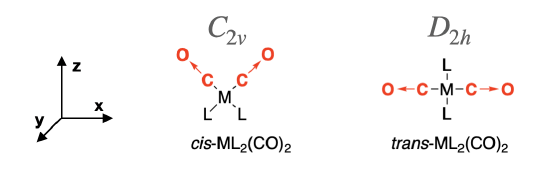
Step 2: Produce a reducible representation (\(\Gamma\)) for CO stretches in each isomer
First, assign a vector along each C—O bond in the molecule to represent the direction of C—O stretching motions, as shown in Figure \(\PageIndex{2}\) (red arrows →). These vectors are used to produce a reducible representation (\(\Gamma\)) for the C—O stretching motions in each molecule. Using the symmetry operations under the appropriate character table, assign a value of 1 to each vector that remains in place during the operation, and a value of 0 if the vector moves out of place. There will be no occasion where a vector remains in place but is inverted, so a value of -1 will not occur.
cis- ML2(CO)2:
For cis- ML2(CO)2, the point group is \(C_{2v}\) and so we use the operations under the \(C_{2v}\) character table to create the \(\Gamma_{cis-CO}\). \[\begin{array}{|c|cccc|} \hline \bf{C_{2v}} & E & C_2 &\sigma_v (xz) & \sigma_v' (yz) \\ \hline \bf{\Gamma_{cis-CO}} & 2 & 0 & 2 & 0 \\ \hline \end{array} \nonumber \]
trans- ML2(CO)2:
For trans- ML2(CO)2, the point group is \(D_{2h}\) and so we use the operations under the \(D_{2h}\) character table to create the \(\Gamma_{trans-CO}\). \[\begin{array}{|c|cccccccc|} \hline \bf{D_{2h}} & E & C_2(z) & C_2(y) &C_2(x) & i &\sigma(xy) & \sigma(xz) & \sigma(yz) \\ \hline \bf{\Gamma_{trans-CO}} & 2 & 0 & 0 & 2 & 0 & 2 & 2 & 0\\ \hline \end{array} \nonumber \]
Step 3: Break each \(\Gamma\) into its component irreducible representations
Each \(\Gamma\) can be reduced using inspection or by the systematic method described previously.
In the case of the cis- ML2(CO)2, the CO stretching vibrations are represented by \(A_1\) and \(B_1\) irreducible representations: \[\begin{array}{|c|cccc|cc|} \hline \bf{C_{2v}} & E & C_2 &\sigma_v (xz) & \sigma_v' (yz) \\ \hline \bf{\Gamma_{cis-CO}} & 2 & 0 & 2 & 0 & & \\ \hline A_1 & 1 & 1 & 1 & 1 & z & x^2, y^2, z^2 \\ B_1 & 1 & -1 & 1 & -1 & x, R_y & xz \\ \hline \end{array} \label{c2v} \]
In the case of trans- ML2(CO)2, the CO stretching vibrations are represented by \(A_1\) and \(B_{3u}\) irreducible representations:
\[\begin{array}{|c|cccccccc|cc|} \hline \bf{D_{2h}} & E & C_2(z) & C_2(y) &C_2(x) & i &\sigma(xy) & \sigma(xz) & \sigma(yz) \\
\hline \bf{\Gamma_{trans-CO}} & 2 & 0 & 0 & 2 & 0 & 2 & 2 & 0 & & \\
\hline A_{g} & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & & x^2, \; y^2, \; z^2\\
B_{3u} & 1 & -1 & -1 & 1 & -1 & 1 & 1 & -1 & x & \\
\hline \end{array} \nonumber \]
These irreducible representations correspond to the symmetries of only the selected C—O vibrations. Since these motions are isolated to the C—O group, they do not include any rotations or translations of the entire molecule, and so we do not need to find and subtract rotationals or translations (unlike the previous cases where all motions were considered).
Step 4: Determine which vibrational modes are IR-active and/or Raman-active
Apply the infrared selection rules described previously to determine which of the CO vibrational motions are IR-active and Raman-active. The two isomers of ML2(CO)2 are described below.
In the case of the cis- ML2(CO)2, the CO stretching vibrations are represented by \(A_1\) and \(B_1\) irreducible representations. The characters of both representations and their functions are shown above, in \ref{c2v} (and can be found in the \(C_{2v}\) character table). Under \(C_{2v}\), both the \(A_1\) and \(B_1\) CO vibrational modes are IR-active and Raman-active. Therefore, two bands in the IR spectrum and two bands in the Raman spectrum are possible.
In the case of the trans- ML2(CO)2, the CO stretching vibrations are represented by \(A_g\) and \(B_{3u}\) irreducible representations. The characters of both representations and their functions are shown above, in \ref{c2v} (and can be found in the \(D_{2h}\) character table). Under \(D_{2h}\), the \(A_g\) vibrational mode is is Raman-active only, while the \(B_{3u}\) vibrational mode is IR-active only. Therefore, only one IR band and one Raman band are possible for this isomer.
Summary
It is possible to distinguish between the two isomers of square planar ML2(CO)2 using either IR or Raman vibrational spectroscopy. The cis- ML2(CO)2 can produce two CO stretches in an IR or Raman spectrum, while the trans- ML2(CO)2 isomer can produce only one band in either type of vibrational spectrum. If a sample of ML2(CO)2 produced two CO stretching bands, we could rule out the possibility of a pure sample of trans-ML2(CO)2.
Repeat the steps outlined above to determine how many CO vibrations are possible for mer-ML3(CO)3 and fac-ML3(CO)3 isomers (see Figure \(\PageIndex{1}\)) in both IR and Raman spectra. Could either of these vibrational spectroscopies be used to distinguish the two isomers?
- Answer
-
Step 1: Assign the point group and Cartesian coordinates for each isomer.
The fac-isomer is \(C_{3v}\). The mer-isomer is \(C_{2v}\).Step 2: Produce a reducible representation for CO stretches in each isomer.
Step 3: Break each into its component irreducible representations.
Step 4: Determine which vibrational modes are IR-active and/or Raman-active.
For fac-ML3(CO)3, the point group is \(C_{3v}\) and so we use the operations under the \(C_{3v}\) character table to create the \(\Gamma_{fac-CO}\). Then break it into its irreducible representations and determine which are IR and Raman active: \[\begin{array}{|c|ccc|} \hline \bf{C_{3v}} & E & 2C_2 &3\sigma_v \\ \hline \bf{\Gamma_{fac-CO}} & 3 & 0 & 1 \\ \hline \end{array} \nonumber \]
This reduces to \(A_1 + E\). Both of these are IR active, and since one is singly degenerate while the other is doubly degenerate, we expect three possible IR bands from this isomer. Both vibrational modes are also Raman active, and again we would expect three possible bands in the Raman spectrum.
For mer-ML3(CO)3, the point group is \(C_{2v}\) and so we use the operations under the \(C_{2v}\) character table to create the \(\Gamma_{mer-CO}\). Then break it into its irreducible representations and determine which are IR and Raman active:
\[\begin{array}{|c|cccc|} \hline \bf{C_{2v}} & E & C_2 &\sigma_v (xz) & \sigma_v' (yz) \\ \hline \bf{\Gamma_{mer-CO}} & 3 & 1 & 3 & 1 \\ \hline \end{array} \nonumber \]This reduces to \(2A_1+B_1\); both \(A_1\) and \(B_1\) are IR and Raman active. So this isomer would have three possible IR bands and three possible Raman Bands.
These two isomers have the same number of possible bands in both IR and Raman spectroscopy. It would not be straightforward to distinguish them from each other based on the number of possible bands in the vibrational spectrum.


