4.3.3: Character Tables
- Page ID
- 227158
Introduction to Character Tables, using \(C_{2v}\) as example
A character table is the complete set of irreducible representations of a symmetry group. In the previous section, we derived three of the four irreducible representations for the \(C_{2v}\) point group. These three irreducible representations are labeled \(A_1\), \(B_1\), and \(B_2\). The fourth irreducible representation, \(A_2\), can be derived using the properties (or "rules") for irreducible representations listed below.
- There is always a totally symmetric representation in which all the characters are 1.
e.g. In \(C_{2v}\), \(A_1\) is totally symmetric. - The order of the group (\(h\)) is the total number of symmetry operations in the group.
e.g. In \(C_{2v}\), \(h=4\) - Similar operations are listed as classes (R) and appear as columns in the table.
e.g. In \(C_{2v}\), there are four classes of operations, \(E\), \(C_2\), \(\sigma_{v(xz)}\), and \(\sigma_{v(yz)}'\) - The number of irreducible representations (rows) must equal the number of classes (columns). This results in all character tables being square.
e.g. In \(C_{2v}\), there are four classes and four irreducible representations. - The sum of squares of all characters under \(E\) is equal to the order of the group: \(h = \sum [\chi_i]^2\)
e.g. In \(C_{2v}\), \(h = 1^2 + 1^2 +1^2 +1^2 = 4\) - For any irreducible representation (\(i\)), the sum of squares of its characters multiplied by the number of operations in the class is the order of the group: \(h = \sum [\chi_i(R)]^2\)
e.g. For \(A_2\) in \(C_{2v}\), \(h = (1\times 1)^2 + (1\times 1)^2 +(-1\times 1)^2 +(-1\times 1)^2 = 4\) - Irreducible representations are orthogonal. For any two representations (\(i\) and \(j\)): \(\sum [\chi_i*(R)\chi_j(R)] = 0\)
e.g. For \(\color{red}B_1\) and \(\color{blue}B_2\) of \(C_{2v}\), \([{\color{red}1} \times {\color{blue}1}] + [{\color{red}-1} \times {\color{blue}-1}] + [{\color{red}1} \times {\color{blue}-1}] + [{\color{red}-1} \times {\color{blue}1}] = 0\)
The complete character table for \(C_{2v}\) is given below.
\(\begin{array}{l|llll|l|l} C_{2v} & E & C_2 & \sigma_v & \sigma_v' & h=4\\ \hline \color{green}A_1 & \color{green}1 & \color{green}1 & \color{green}1 & \color{green}1 & \color{green}z & x^2,y^2,z^2\\ \color{purple}A_2 & \color{purple}1 & \color{purple}1 & \color{purple}-1 & \color{purple}-1 & R_z & xy \\ \color{red}B_1 & \color{red}1 & \color{red}-1&\color{red}1&\color{red}-1 & {\color{red}x},R_y & xz \\ \color{blue}B_2 & \color{blue}1 & \color{blue}-1 & \color{blue}-1 & \color{blue}1 & {\color{blue}y} ,R_x & yz \end{array} \)
The various sections of the table are as follows:
- The first element in the table gives the name of the point group, usually in Schoenflies (\(C_{2v}\)) notation.
- Along the first row are the symmetry operations of the group, \(E\), \(C_2\), \(\sigma_v\) and \(\sigma_v"\), followed by the order of the group, \(h\).
- In the first column are the irreducible representations of the group, represented by Mulliken Labels. In \(C_{2v}\) the irreducible representations are \(A_1\), \(A_2\), \(B_1\) and \(B_2\). The Mulliken labels indicate the symmetry of each representation (explained further below).
- The characters (\(\chi\)) of the irreducible representations under each symmetry operation are given in the bulk of the table.
- The final column(s) of the table lists a number of functions that transform as the various irreducible representations of the group. These are the Cartesian axes \(\begin{pmatrix} x, y, z \end{pmatrix}\), the Cartesian products \(\begin{pmatrix} z^2, x^2 + y^2, xy, xz, yz \end{pmatrix}\), and the rotations \(\begin{pmatrix} R_x, R_y, R_z \end{pmatrix}\) (explained further below).
Another example: \(C_{3v}\)
Th \(C_{3v}\) point group has three classes of operations: \(E\), \(C_{3}\), and \(\sigma_{v(xz)}\). The derivation of transformation matrices for E and \(\sigma_{v(xz)}\) is similar to the case for \(C_{2v}\). However, the \(C_{3v}\) operation does not give simple 1 or -1 characters. If we carry out a rotation about \(z\) by an angle \(\theta\), our \(x\) and \(y\) axes are transformed onto new axes \(x'\) and \(y'\). The new axes can each be written as a linear combination of our original \(x\) and \(y\) axes. The derivation of the rotation matrices will not be covered in this text, but is described elsewhere:
\[\begin{array}{ccc}x' & = & x\cos\theta + y\sin\theta \\ y' & = & -x\sin\theta + y\cos\theta \end{array} \nonumber \]
For a \(C_3\) rotation counterclockwise through 120° (or \(\frac{2\pi}{3}\)):
\[\begin{array}{ccccc}x' & = & x\cos(2\pi/3) + y\sin(2\pi/3) & = & {\color{orange}-\frac{1}{2}x-\frac{\sqrt{3}}{2}y} \\ y' & = & -x\sin(2\pi/3) + y\cos(2\pi/3) & = & {\color{violet}\frac{\sqrt{3}}{2}x-\frac{1}{2}y} \end{array} \nonumber \]
The transformation matrices for symmetry operations of \(C_{3v}\) are as follows:
\(E=\begin{pmatrix} 1&0&0 \\ 0&1&0 \\ 0&0&1 \end{pmatrix} \nonumber\) \(C_3=\begin{pmatrix} {\color{orange}[-\frac{1}{2}}&{\color{orange}-\frac{\sqrt{3}}{2}]}&0 \\ {\color{violet}[\frac{\sqrt{3}}{2}}&{\color{violet}-\frac{1}{2}]}&0 \\ 0&0&1 \end{pmatrix} \nonumber\) \(\sigma_{v(xz)}'=\begin{pmatrix} 1&0&0 \\ 0&-1&0 \\ 0&0&1 \end{pmatrix} \nonumber\)
The \(C_3\) transformation matrix contains off-diagonal entries, and therefore it cannot be block diagonalized as 1x1 matrices. However, the first two lines can be diagonalized as a 2x2 and the last line as a 1x1 matrix (Figure \(\PageIndex{1}\)):
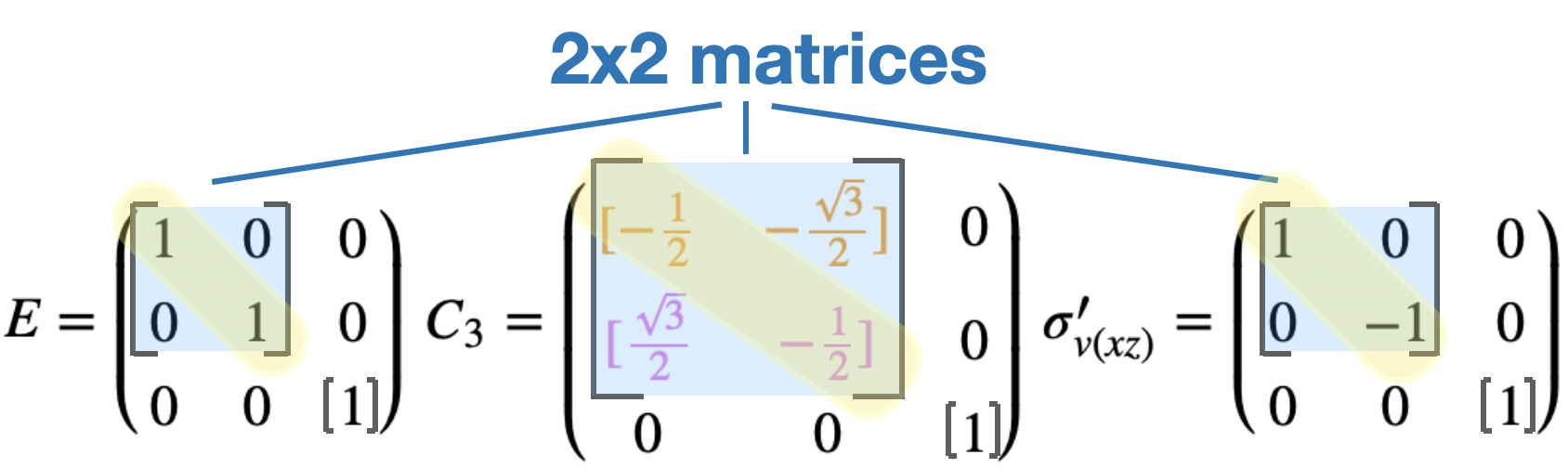
The character from a 2x2 matrix is the sum of the trace of that matrix. So, for the \(C_3\) operation, the 2x2 matrix gives the character -1 (from \({\color{orange}-\frac{1}{2}} + {\color{violet}-\frac{1}{2}}\)).
The character table for \(C_{3v}\) is shown below.
\(\begin{array}{l|lll|l} \hline C_{3v} & E & 2C_3 & 3\sigma_v & h=6 \\ \hline A_1 & 1 & 1 & 1 & z, z^2, x^2+y^2 \\ A_2 & 1 & 1 & -1 & R_z \\ E & 2 & -1 & 0 & \begin{pmatrix} x, y \end{pmatrix}, \begin{pmatrix} xy, x^2+y^2 \end{pmatrix}, \begin{pmatrix} xz, yz \end{pmatrix}, \begin{pmatrix} R_x, R_y \end{pmatrix} \\ \hline \end{array} \)
Additional features of character tables
- Symmetry operations of the same class are grouped into the same column (class) in the character table and not listed separately.
e.g. In the \(C_{3v}\) point group, there are four operations: \(E\), \(C_3\), \(C_3^2\), and \(\sigma_{v}\). The \(C_3\) and \(C_3^2\) operations are listed together in the character table as \(2C_3\). - IF there are multiple \(C_2\) axes (in a \(D\) group), the \(C_2\) axes that are perpendicular to the principle axis are labeled with primes (e.g. \(C_2'\) and \(C_2''\)); when there are multiple types of perpendicular \(C_2\) axes, one prime (\(C_2'\)) means that it passes through more atoms, while a double prime (\(C_2''\)) means it goes between atoms.
- Mirror planes that are perpendicular to the principle axis are "horizontal" mirror planes and are designated with an \(h\) subscript (\(\sigma_h\)). Mirror planes that are in-plane with the principle axis are "vertical" mirror planes, \(\sigma_v\). When there are two types of vertical mirror planes, those that run through more atoms are \(\sigma_v\) while those that run between atoms are "dihedral", \(\sigma_d\).
- Matching the symmetry operations listed in the character table to the symmetry operations of a molecule can confirm its point group.
- Irreducible representations are each assigned a Mulliken label, listed in the left-hand column, that indicates the symmetry of that representation as follows:
\(\begin{array}{l|l} \hline \textbf{Mulliken Labels} & \textbf{meaning}\\ \hline A & \text{singly degenerate (1x1), symmetric to principle axis} \\ B & \text{singly degenerate (1x1), antisymmetric to principle axis} \\ E & \text{doubly degenerate (2x2)} \\ T & \text{triply degenerate (3x3)} \\ \hline \textbf{Subscripts and superscripts} & \textbf{meaning} \\ \hline 1 & \text{symmetric to } \sigma_v \text{or perpendicular to } C_2 \\ 2 & \text{anti-symmetric to } \sigma_v \text{or perpendicular to } C_2 \\ g & \text{symmetric to inversion center} \\ u & \text{anti-symmetric to inversion center} \\ ' & \text{symmetric to } \sigma_h \\ " & \text{anti-symmetric to } \sigma_h \\ \hline \end{array} \) - The right-hand columns of the character table list a number of functions that transform as the various irreducible representations of the group. These are the Cartesian axes \(\begin{pmatrix} x, y, z \end{pmatrix}\), the Cartesian products \(\begin{pmatrix} z^2, x^2 + y^2, xy, xz, yz \end{pmatrix}\), and the rotations \(\begin{pmatrix} R_x, R_y, R_z \end{pmatrix}\). These expressions indicate the properties of orbitals within the symmetry group. The \(s\)-orbital, which is totally symmetric, corresponds to the irreducible representation that possesses symmetry of \(x^2\), \(y^2\) and \(z^2\) combined. The \(p\)-orbitals each possess the symmetry of the corresponding axis (e.g. \(p_x\) corresponds to the \(x\) axis). Each of the \(d\)-orbitals possess the symmetry of the corresponding binary product (e.g. \(d_{xy}\) corresponds to the binary product, \(xy\), in the character table).
The functions listed in the final column of the table are important in many chemical applications of group theory, particularly in spectroscopy. For example, by looking at the transformation properties of \(x\), \(y\) and \(z\) (sometimes given in character tables as \(T_x\), \(T_y\), \(T_z\)) we can discover the symmetry of translations along the \(x\), \(y\), and \(z\) axes. Similarly, \(R_x\), \(R_y\) and \(R_z\) represent rotations about the three Cartesian axes. The transformation properties of \(x\), \(y\), and \(z\) can be used to determine whether or not a molecule is IR-active or whether or not it can absorb a photon of \(x\)-, \(y\)-, or \(z\)-polarized light and undergo a spectroscopic transition. The Cartesian products play a similar role in determining selection rules for Raman transitions, which involve two photons.
A visual summary of the sections and their significance is given in Figure \(\PageIndex{2}\). Character tables for common point groups are given in the References section of LibreTexts Bookshelves.

Contributors and Attributions
Curated or created by Kathryn Haas
Claire Vallance (University of Oxford)
adapted from Character Tables (click here)


