19.8F: Stereoisomerism - Enantiomers
- Last updated
- Save as PDF
- Page ID
- 34368
Optical activity refers to whether or not a compound has optical isomers. A coordinate compound that is optically active has optical isomers and a coordinate compound that is not optically active does not have optical isomers. As we will discuss later, optical isomers have the unique property of rotating light. When light is shot through a polarimeter, optical isomers can rotate the light so it comes out in a different direction on the other end. Armed with the knowledge of symmetry and mirror images, optical isomers should not be very difficult. There are two ways optical isomers can be determined: using mirror images or using planes of symmetry.
Optical isomers do not exhibit symmetry and do not have identical mirror images. Let's go through a quick review of symmetry and mirror images. A mirror image of an object is that object flipped or the way the object would look in front of a mirror. For example, the mirror image of your left hand would be your right hand. Symmetry on the other hand refers to when an object looks exactly the same when sliced in a certain direction with a plane. For example imagine the shape of a square. No matter in what direction it is sliced, the two resulting images will be the same.
Method 1: The "Mirror Image Method"
The mirror images method uses a mirror image of the molecule to determined whether optical isomers exist or not. If the mirror image can be rotated in such a way that it looks identical to the original molecule, then the molecule is said to be superimposable and has no optical isomers. On the other hand, if the mirror image cannot be rotated in any way such that it looks identical to the original molecule, then the molecule is said to be non-superimposable and the molecule has optical isomers. Once again, if the mirror image is superimposable, then no optical isomers but if the mirror image is non-superimposable, then optical isomers exist.
Definition: Non-superimposable
Non-superimposable means the structure cannot be rotated in a way that one can be put on top of another. This means that no matter how the structure is rotated, it cannot be put on top of another with all points matching. An example of this is your hands. Both left and right hands are identical, but they cannot be put on top of each other with all points matching.
The examples you are most likely to need occur in octahedral complexes which contain bidentate ligands - ions like \([Ni(NH_2CH_2CH_2NH_2)_3]^{2+}\) or \([Cr(C_2O_4)_3]^{3-}\). The diagram below shows a simplified view of one of these ions. Essentially, they all have the same shape - all that differs is the nature of the "headphones".
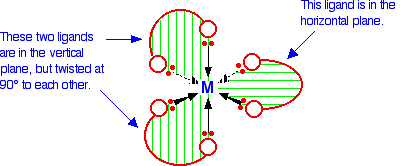
A substance with no plane of symmetry is going to have optical isomers - one of which is the mirror image of the other. One of the isomers will rotate the plane of polarization of plane polarised light clockwise; the other rotates it counter-clockwise. In this case, the two isomers are:
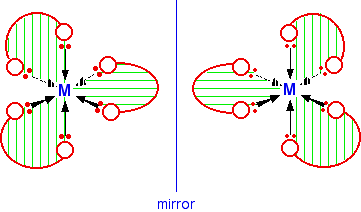
You may be able to see that there is no way of rotating the second isomer in space so that it looks exactly the same as the first one. As long as you draw the isomers carefully, with the second one a true reflection of the first, the two structures will be different.
Method 2: The "Plane of Symmetry Method"
The plane of symmetry method uses symmetry, as it's name indicates, to identify optical isomers. In this method, one tries to see if such a plane exists which when cut through the coordinate compound produces two exact images. In other words, one looks for the existence of a plane of symmetry within the coordinate compound. If a plane of symmetry exists, then no optical isomers exist. On the other hand, if there is no plane of symmetry, the coordinate compound has optical isomers. Furthermore, if a plane of symmetry exists around the central atom, then that molecule is called achiral but if a plane of symmetry does not exist around the central molecule, then that molecule has chiral center.
Example \(\PageIndex{1}\): CHBrClF
Consider the tetrahedral molecule, CHBrClF (note the color scheme: grey=carbon, white=hydrogen, green=chlorine, blue=fluorine, red=bromine)
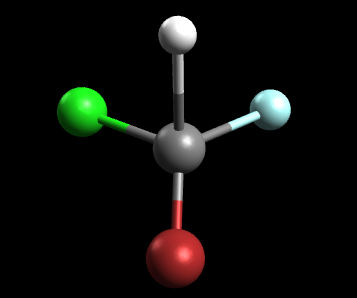
Is this molecule optically active? In other words, does this molecule have optical isomers?
Solution
First take the Mirror-image method. The mirror image of the molecule is:
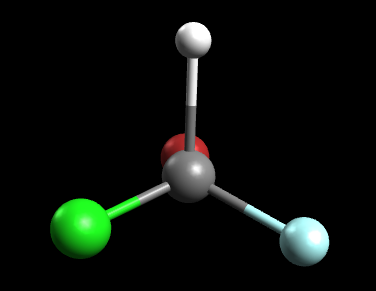
Note that this mirror image is not superimposable. In other words, the mirror image above cannot be rotated in any such way that it looks identical to the original molecule. Remember, if the mirror image is not superimposable, then optical isomers exist. Thus we know that this molecule has optical isomers.
Let's try approaching this problem using the symmetry method. If we take the original molecule and draw an axis or plane of symmetry down the middle, this is what we get:
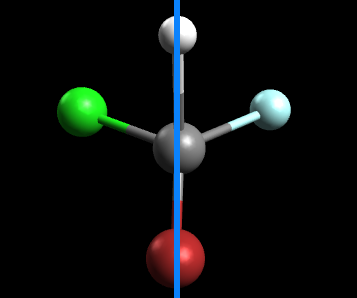
Since the left side is not identical to the right, this molecule does not have a symmetrical center and thus can be called chiral.Additionally, because it does not have a symmetrical center, we can conclude that this molecule has optical isomers. In general, when dealing with a tetrahedral molecule that has 4 different ligands, optical isomers will exist most of the time.
No matter which method you use, the answer will end up being the same.
Optical isomers because they have no plane of symmetry. In the organic case, for tetrahedral complexes, this is fairly easy to recognize the possibility of this by looking for a center atom with four different things attached to it. Unfortunately, this is not quite so easy with more complicated geometries!
Example \(\PageIndex{1}\): \(\ce{PFeCl3F3}\)
This time we will be analyzing the octahedral compound FeCl3F3. Is this molecule optically active?
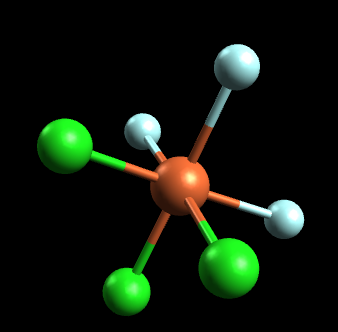
(note the color scheme: orange=iron, blue=fluorine, green=chlorine):
Solution
If we try to attempt this problem using the mirror image method, we notice that the mirror image is essentially identical to the original molecule. In other words, the mirror image can be placed on top of the original molecule and is thus superimposable. Since the mirror image is superimposable, this molecule does not have any optical isomers. Let's attempt this same problem using the symmetry method. If we draw an axis or plane of symmetry, this is what we get:
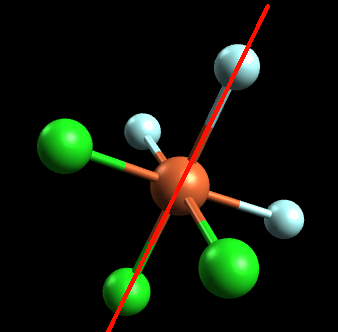
Since the left side is identical to the right side, this molecule has a symmetrical center and is an achiral molecule. Thus, it has no optical isomers.
What is a Polarimeter?
A polarimeter is a scientific instrument used to measure the angle of rotation caused by passing polarized light through an optically active substance. Some chemical substances are optically active, and polarized (uni-directional) light will rotate either to the left (counter-clockwise) or right (clockwise) when passed through these substances. The amount by which the light is rotated is known as the angle of rotation. The angle of rotation is basically known as observed angle.
.svg.png?revision=1&size=bestfit&width=695&height=386)
The polarimeter is made up of a polarizer (#3 on Figure \(\PageIndex{1}\)) and an analyzer (#7 on Figure \(\PageIndex{1}\)). The polarizer allows only those light waves which move in a single plane. This causes the light to become plane polarized. When the analyzer is also placed in a similar position it allows the light waves coming from the polarizer to pass through it. When it is rotated through the right angle no waves can pass through the right angle and the field appears to be dark. If now a glass tube containing an optically active solution is placed between the polarizer and analyzer the light now rotates through the plane of polarization through a certain angle, the analyzer will have to be rotated in same angle.
Nomenclature of Optical Isomers
Various methods have been used to denote the absolute configuration of optical isomers such as R or S, Λ or Δ, or C and A. The IUPAC rules suggest that for general octahedral complexes C/A scheme is convenient to use and that for bis and tris bidentate complexes the absolute configuration be designated Lambda Λ (left-handed) and Delta Δ (right-handed).
Priorities are assigned for mononuclear coordination systems based on the standard sequence rules developed for enantiomeric carbon compounds by Cahn, Ingold and Prelog (CIP rules). These rules use the coordinating atom to arrange the ligands into a priority order such that the highest atomic number gives the highest priority number (smallest CIP number). For example the hypothetical complex [Co Cl Br I NH3 NO2 SCN]2- would assign the I- as 1, Br as 2, Cl as 3, SCN as 4, NO2 as 5 and NH3 as 6.

Figure \(\PageIndex{2}\): Here is one isomer where the I and Cl, and Br and NO2 were found to be trans- to each other.
The reference axis for an octahedral center is that axis containing the ligating atom of CIP priority 1 and the trans ligating atom of lowest possible priority (highest numerical value). The atoms in the coordination plane perpendicular to the reference axis are viewed from the ligand having that highest priority (CIP priority 1) and the clockwise and anticlockwise sequences of priority numbers are compared. The structure is assigned the symbol C or A, according to whether the clockwise (C) or anticlockwise (A) sequence is lower at the first point of difference. In the example shown above this would be C.

The two optical isomers of [Co(en)3]3+ have identical chemical properties and just denoting their absolute configuration does NOT give any information regarding the direction in which they rotate plane-polarised light. This can ONLY be determined from measurement and then the isomers are further distinguished by using the prefixes (-) and (+) depending on whether they rotate left or right.
3_isomers.jpg?revision=1)
To add to the confusion, when measured at the sodium D line (589 nm), the tris(1,2-diaminoethane)M(III) complexes (M= Rh(III) and Co(III)) with IDENTICAL absolute configuration, rotate plane polarized light in OPPOSITE directions! The left-handed (Λ)-[Co(en)3]3+ isomer gives a rotation to the right and therefore corresponds to the (+) isomer. Since the successful resolution of an entirely inorganic ion (containing no C atoms) (hexol) only a handful of truly inorganic complexes have been isolated as their optical isomers e.g. (NH4)2Pt(S5)3.2H2O.
For tetrahedral complexes, R and S would be used in a similar method to tetrahedral Carbon species and although it is predicted that tetrahedral complexes with 4 different ligands should be able to give rise to optical isomers, in general they are too labile and can not be isolated.
Contributors and Attributions
Prof. Robert J. Lancashire (The Department of Chemistry, University of the West Indies)
Jim Clark (Chemguide.co.uk)

